Основные законы и формулы
| Закон Кулона | 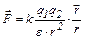
|
| Напряжённость электрического поля | 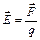 
|
| Теорема Остроградского – Гаусса | 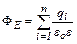
|
| Напряжённость поля: - точечного заряда | 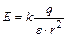
|
| - созданного двумя (и более) точечными зарядами | 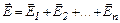
|
| - созданного бесконечной равномерно заряженной плоскостью | 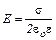
|
| - поверхностная плотность заряда | 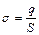
|
| Потенциальная энергия взаимодействия точечных зарядов | 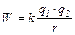
|
| Потенциал поля | 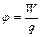
|
| Потенциал поля точечного заряда | 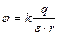
|
| Работа, совершаемая электрическим полем при перемещении точечного заряда q | 
|
| Связь между напряжённостью и потенциалом неоднородного и однородного полей | 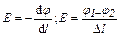
|
| Электроёмкость: - уединённого проводника, конденсатора | 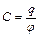 ; ; 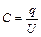
|
| - плоского конденсатора | 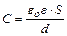
|
| - последовательно соединённых конденсаторов | 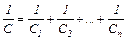
|
| - параллельно соединённых конденсаторов | C = C1 + C2 +... + Cn |
| Энергия конденсатора | 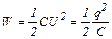
|
| Объёмная плотность энергии электрического поля | 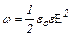
|
| Сила постоянного тока | 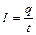
|
| Плотность тока | 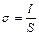
|
| Закон Ома для однородного участка цепи | 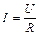
|
| Закон Ома для замкнутой цепи | 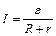
|
| Сопротивление однородного проводника | 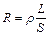
|
| Ток короткого замыкания | 
|
| Мощность тока | N = IU = I2R |
| Закон Джоуля – Ленца | Q = I2Rt |
Примеры решения задач
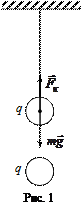 Пример 1. На непроводящей нити в воздухе подвешен шарик массой т = 100 мг, несущий заряд q. Если снизу на расстоянии r = 4 см поместить шарик с таким же зарядом, натяжение нити Т исчезнет. Определить величину заряда шарика.
Пример 1. На непроводящей нити в воздухе подвешен шарик массой т = 100 мг, несущий заряд q. Если снизу на расстоянии r = 4 см поместить шарик с таким же зарядом, натяжение нити Т исчезнет. Определить величину заряда шарика.
Дано: m = 100 мг = 10-4 кг;
r = 4 см = 0,04 м.
Найти: q.
Решение: По условию задачи, шарик находится в равновесии под действием силы тяжести mg и силы кулоновского отталкивания Fк (рис. 1):
mg = Fк,(1)
Выразим в соответствии с законом Кулона силу Fк:
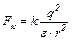 , (2)
, (2)
где ε = 1 – диэлектрическая проницаемость воздуха, k = 9·109 м/Ф – коэффициент пропорциональности в законе Кулона.
Подставив (2) в (1), получим:
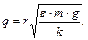 (3)
(3)
Вычислим искомый заряд: 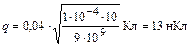 .
.
Ответ: q = 13 нКл.
Пример 2. Два положительных заряда q1 = 7 нКл и q2 = 4 нКл находятся на расстоянии r = 15 см друг от друга. Определить положение точки, в которую нужно поместить заряд q3, чтобы он находился в равновесии. Каков должен быть знак заряда q3, чтобы равновесие было устойчивым?
| Дано: q1= 7 нКл = 7·10-9 Кл; q2 = 4 нКл = 4·10-9 Кл; r = 15 см = 0,15 м. Найти: x. | 
|
Решение: Рассмотрим вопрос об устойчивости равновесия заряда q3. Если заряд q3 будет находиться на линии, соединяющей заряды q1 и q2, то, каков бы ни был знак заряда q3, силы его взаимодействия с зарядами q1 и q2 будут направлены по одной прямой в противоположные стороны. Следовательно, точка находится на прямой АВ (рис. 2), в которой силы будут уравновешены.
Пусть такая точка находится между зарядами q1 и q2 на расстоянии х от заряда q1. При отклонении заряда q3 от этой точки вправо или влево возникающее неравенство сил со стороны зарядов q1 и q2 будет неизменно возвращать заряд q3 в положение равновесия. Рассмотрим теперь случай отклонения заряда q3 перпендикулярно линии АВ. В этом случае, если заряд положительный, при отклонении его вверх или вниз от положения равновесия силы отталкивания его зарядами q1 и q2 создадут равнодействующую, отбрасывающую заряд от линии АВ, на которой находится точка равновесия. Следовательно, при q3>0 положение равновесия не будет устойчивым. Если заряд q3 отрицательный, то при его отклонении вверх или вниз от положения равновесия силы притяжения его зарядами q1 и q2 создают равнодействующую силу, возвращающую заряд q3 на линию АВ. В этом случае равновесие заряда устойчивое [2].
При равновесии заряда q3 силы F1 и F2,действующие со стороны зарядов q1 и q2, равны между собой:
F1 = F2. (1)
Выразив F1 и F2 из закона Кулона, получим
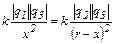 , или
, или 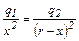 .
.
Извлекая из обеих частей равенства квадратный корень, имеем
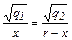 .
.
Откуда
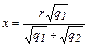 . (2)
. (2)
Вычислим искомое расстояние:
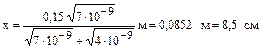 .
.
Ответ: Точка, в которую нужно поместить заряд q3,находится на расстоянии 8,5 см от заряда q1 .
Пример 3. Два заряда q1 = 9 нКл и q2 = –7 нКл расположены в вершинах равностороннего треугольника со стороной a = 20 см. Определить напряжённость и потенциал электрического поля в третьей вершине треугольника.
| Дано: q1 = 9 нКл = 9·10-9 Кл; q2 = –7 нКл = –7·10-9 Кл; a = 20 см = 0,2м; β = 60o. Найти: Е, j. | 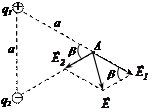 Рис. 3 Рис. 3
|
Решение: По принципусуперпозиции полей напряжённость электрического поля в точке А (рис. 3) равна геометрической (т.е. векторной) суммой напряжённостей 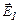 и
и 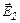 полей, создаваемых зарядами q1 и q2 соответственно:
полей, создаваемых зарядами q1 и q2 соответственно:
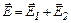 .
.
Модуль результирующей напряжённости найдём по теореме косинусов, как диагональ параллелограмма, построенного на векторах 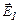 и
и 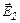
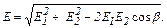 (1)
(1)
Напряжённость электрического поля точечного заряда выражается формулой
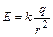 , (2)
, (2)
где q – заряд, создающий поле; k – коэффициент пропорциональности в законе Кулона; r – расстояние от заряда до рассматриваемой точки поля.
Так как r = r1 = r2 = a, то имеем
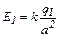 ,
, 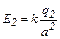 . (3)
. (3)
Подставив (3) в (1), получим
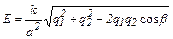 . (4)
. (4)
Вычислим напряженность поля в точке А
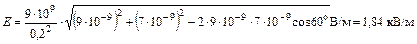 .
.
Потенциал электрического поля в точке А равен алгебраической сумме потенциалов j1 и j2 полей, создаваемых зарядами q1 и q2 соответственно:
j = j1 + j2. (5)
Потенциал поля точечного заряда
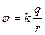 . (6)
. (6)
В формуле (6) обозначения те же, что и в формуле (2). Подставив (6) в (5) и учитывая, что r = r1 = r2 = а, получим
 . (7)
. (7)
Подставим числовые значения величин в (7) и определим результирующий потенциал в точке А: 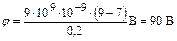 .
.
Ответ: Е = 1,84 кВ/м; j = 90 B.
Пример 4. Электростатическое поле создано двумя заряженными пластинами с зарядами q1 = 16 нКл, q2 = –4нКл. Площади пластин
S1 = S2 = 0,04 м2, расстояние между ними d = 0,5 см. Определить напряжённость поля, между пластинами и вне их. Построить график изменения напряжённости вдоль оси, перпендикулярной пластинам, считая напряжённость положительной, если её вектор направлен слева направо. Найти разность потенциалов между пластинами U.
| Дано: q1 = 16 нКл = 16·10-9Кл; q2 = - 4 нКл = - 4· 10-9 Кл; S1 = S2 =0,04м2; d = 0,5 см = 5·10-3м. Найти: ЕI; EII; EIII; U. |  Рис. 4 Рис. 4
|
Решение: На рис. 4а изображены заряженные пластины и силовые линии полей: сплошные – силовые линии первой пластины, пунктирные – второй пластины.
Напряжённости электрических по-лей, создаваемых пластинами, которые считаем бесконечно большими равномерно заряженными плоскостями, соответственно равны:
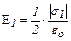 , , 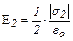 , (1) , (1)
|
где s1 и s2 – поверхностные плотности зарядов пластин; eo = 8,85×10–12 Ф/м – электрическая постоянная.
По определению:
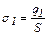 ,
, 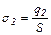 . (2)
. (2)
Согласно принципу суперпозиции, поля, создаваемые каждой заряженной плоскостью, накладываются друг на друга, причем каждая заряженная плоскость создает электрическое поле независимо от присутствия другой
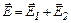 . (3)
. (3)
Плоскости делят всё пространство на три области: I, II, III. Как видно из рис. 4а, в первой и третьей областях векторы 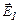 и
и 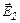 направлены в противоположные стороны. В проекции на ось Ох напряженности полей в I и III областях соответственно равны:
направлены в противоположные стороны. В проекции на ось Ох напряженности полей в I и III областях соответственно равны:
 , (4)
, (4)
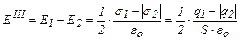 . (5)
. (5)
Между пластинами силовые линии полей направлены в одну сторону, следовательно:
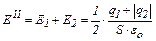 . (6)
. (6)
Подставим числовые значения в (4), (5), и (6) и вычислим напряжённости результирующего поля вне и между пластинами:
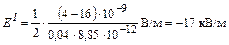 ,
,
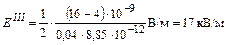 ,
, 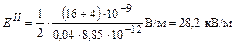 .
.
График распределения напряжённостей суммарного поля представлен на рис. 4б.
Напряжённость однородного электрического поля связана с разностью потенциалов между пластинами соотношением
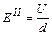 . (6)
. (6)
Откуда
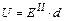 . (7)
. (7)
Определим значение разности потенциалов между пластинами:
U = 28,3 × 103 × 5 × 10-3В = 141 В.
Ответ: EI = –17 кВ/м; EIII = 17 кВ/м; ЕII = 28,2 кВ/м; U = 141 В.
Пример 5. Четыре одноимённых точечных заряда величиной q расположены в вершинах квадрата со стороной а. Какую работу надо совершить, чтобы поместить их в вершины тетраэдра с ребром, равным а?
| Дано: q; а. Найти: А. |
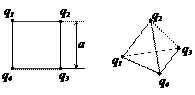 а) б)
Рис. 5 а) б)
Рис. 5
|
Решение: Потенциальная энергия системы зарядов равна сумме энергий попарно взаимодействующих зарядов. Для первой конфигурации зарядов (рис. 5а) потенциальная энергия
WI = W1,2 + W1,3 + W1,4 + W2,3 + W2,4 +W3,4. (1)
По условию задачи q1 = q2 = q3 = q4, поэтому
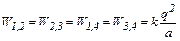 , (2)
, (2)
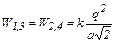 . (3)
. (3)
Следовательно,
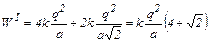 . (4)
. (4)
Для второй конфигурации (рис. 5б) потенциальная энергия взаимодействия зарядов
WII = W1,2 + W1,3 + W1,4 + W2,3 + W2,4 + W3,4 . (5)
Так как расстояния между вершинами в тетраэдре одинаковые и равны а, то
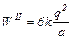 . (6)
. (6)
Работа по перемещению зарядов из одной конфигурации в другую равна разности потенциальных энергий
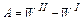 . (7)
. (7)
Подставив в (7) выражения (4) и (5), получим:
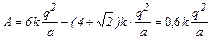 .
.
Ответ: 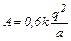 .
.
Пример 6. Шарик массой m = 1 г перемещается из точки 1, потенциал которой φ1 = 600 B, в точку 2, потенциал которой равен нулю. На сколько изменилась при этом скорость шарика, если в точке 2 его скорость возросла до u2 = 20 см/с. Заряд шарика q = 10 нКл.
| Дано: m = 10-3 кг; u2 = 20 см/с = 0,2 м/с; j1 = 600 B; j2 = 0; q = 10 нКл = 10-8 Кл. Найти:Δ u = u2 - u1. |
Решение: На заряженный шарик при его движении в электрическом поле со стороны поля действует сила, работа которой равна изменению кинетической энергии шарика
А = Δ Wк. (1)
Работа, совершаемая электрическим полем при перемещении заряда из точки с потенциалом j1 в точку с потенциалом j2:
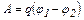 . (2)
. (2)
Изменение кинетической энергии шарика
 . (3)
. (3)
Следовательно, уравнение (1) можно привести к виду
 , (4)
, (4)
тогда
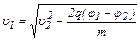 . (5)
. (5)
Подставив числовые значения величин в (5), получим
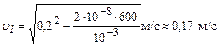 .
.
Изменение скорости шарика Δ u = u2 - u1 = 0,03 м/c.
Ответ: Скорость шарика увеличилась на 0,03 м/с.
Пример 7. Плоский воздушный конденсатор, расстояние между пластинами которого d = 10 см, заряжен до разности потенциалов
U0 = 250 В и отключен от источника. Площадь его пластин S = 100 см2. Определить заряд конденсатора. Во сколько раз изменятся ёмкость, разность потенциалов, энергия конденсатора, если в пространство между пластинами внести стеклянную пластинку толщиной d2 = 8 см и прижать её к одной из пластин конденсатора?
| Дано: d = 10 см = 0,1 м; U0 = 250 B; S = 100 см2 = 10-2 м2; d2 = 8 см = 0,08 м; e1 = 1; e2 = 6. Найти: q; C/Co; U/Uo; W/Wo. | 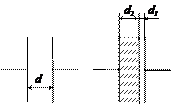 а) б)
Рис. 6 а) б)
Рис. 6
|
Решение: По определению электроёмкость конденсатора равна отношению заряда конденсатора к разности потенциалов между пластинами:
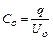 . (1)
. (1)
Зависимость ёмкости плоского конденсатора от его размеров выражается формулой
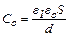 , (2)
, (2)
где e1 = 1 – диэлектрическая проницаемость воздуха; eo = 8,85∙10-12 Ф/м – электрическая постоянная.
Из формул (1) и (2) находим искомый заряд
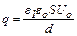 . (3)
. (3)
С учётом числовых значений заряд конденсатора
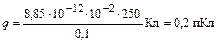 .
.
Если параллельно обкладкам плоского конденсатора ввести слой диэлектрика, частично заполняющего воздушную прослойку, и прижать к одной из пластин, то полученную систему можно рассматривать как два соединённых последовательно конденсатора ёмкостями С1 и С2. Диэлектрик одного конденсатора – воздух толщиной d1 = 0,02 м. Диэлектрик другого конденсатора – стеклянная пластинка с диэлектрической проницаемостью e2 = 6 и толщиной d2 = 0,08 м.
Ёмкость двух последовательно соединённых конденсаторов
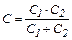 . (4)
. (4)
Подставляя в формулу (4) выражения 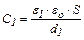 и
и 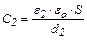 , получим:
, получим:
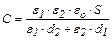 . (5)
. (5)
Из формулы (5) видно, что изменение типа диэлектрика и расстояния между пластинами конденсатора приводит к изменению его ёмкости. Разделив выражение (5) на (2) и подставив числовые значения, имеем 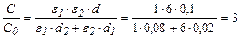 .
.
Ёмкость конденсатора увеличилась в 3 раза.
Из формулы (1) находим разности потенциалов для начального и конечного состояний конденсатора 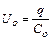 ,
, 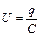 , откуда
, откуда
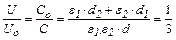 .
.
Напряжение на конденсаторе уменьшается в 3 раза.
Энергия поля конденсатора в его начальном и конечном состояниях выражается формулами:
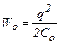 ,
, 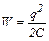 . (6)
. (6)
Отношение энергий
 . (7)
. (7)
Энергия конденсатора уменьшается в 3 раза.
Ответ: q = 0,2 пКл; ёмкость конденсатора увеличилась в 3 раза; напряжение на конденсаторе и его энергия уменьшились в 3 раза.
Пример 8. Три одинаковых источника тока с эдс e = 1,5 В каждый соединены параллельно и создают в цепи ток I = 1 А. Определить коэффициент полезного действия h батареи, если внутреннее сопротивление каждого источника тока r1=r2 =r3= r = 0,3 Ом.
| Дано: e = 1,5 В; I = 1 A; r = 0,3 Ом. Найти: h. |  Рис. 7
Рис. 7
|
Решение: При параллельном подключении одинаковых источников тока электродвижущая сила батареи равна эдс одного источника, общее сопротивление rб определяем по формуле
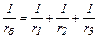 . (1)
. (1)
Поскольку r1 = r2 = r3 = r, формулу (1) можем записать в виде
rб = r / 3. (2)
Батарея источников тока замыкается потребителем электроэнергии, сопротивление которого R. На основании закона Ома для замкнутой цепи
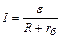 . (3)
. (3)
Отсюда
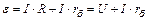 , (4)
, (4)
где U – разность потенциалов на зажимах батареи источников тока.
Из выражения (4) найдём
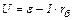 . (5)
. (5)
Коэффициент полезного действия батареи
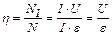 , (6)
, (6)
где N1 = I×U – полезная мощность тока в потребителе; N = I×ε – полная (затраченная) мощность батареи.
С учётом (2) и (5) формула (6) примет вид
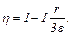 (7)
(7)
Следовательно, 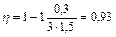 .
.
Ответ: η = 93%.
Пример 9. Электродвигатель работает в сети с напряжением
U = 120 В. Номинальная мощность двигателя N = l,2 кВт, коэффициент полезного действия η = 75 %. Определить силу тока, потребляемую двигателем, и сопротивление его обмоток.
| Дано: U = 120 B; N = 1,2 кВт = 1,2·103 Вт; h = 75 %. Найти: I, r. |
Решение: Мощность двигателя
N = IU, (1)
где I – сила тока, потребляемая двигателем.
Отсюда
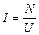 . (2)
. (2)
Подставим значения величин в расчётную формулу и вычислим силу тока 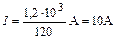 .
.
Коэффициент полезного действия двигателя
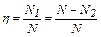 , (3)
, (3)
где N1 – полезная мощность, N2 – мощность, расходуемая на нагревание обмоток двигателя.
Мощность потерь
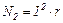 , (4)
, (4)
где r – сопротивление обмоток.
На основании формулы (4) равенство (3) примет вид
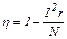 .
.
Откуда
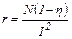 . (5)
. (5)
Рассчитаем сопротивление обмотки электродвигателя 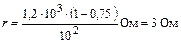 .
.
Ответ: I = 10 A; r = 3 Ом.
Пример 10. Предохранитель изготовлен из свинцовой проволоки сечением S = 0,2 мм2. Найти ток короткого замыкания, если предохранитель перегорел через 0,2 с. Начальная температура предохранителя
t0 = 27 оС.
| Дано: S = 0,2 мм2 = 2·10-5 м2; t = 0,2 с; to = 27 oC. Найти: Iкз. |
Решение: По закону Джоуля-Ленца количество теплоты, выделяющееся в предохранителе за время t,
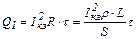 , (1)
, (1)
где r = 21·10-8 Ом·м – удельное сопротивление свинца, L – длина проволки.
Количество теплоты, необходимое для нагревания свинцового предохранителя до точки плавления,
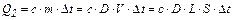 , (2)
, (2)
где с = 130 Дж/кг·oС – удельная теплоёмкость свинца; D = 11300 кг/м3 – плотность свинца; Δ t – изменение температуры от to до температуры плавления tпл = 327 ºC.
При перегорании предохранителя плавится очень короткий отрезок проволоки, поэтому количество теплоты, необходимое для плавления предохранителя, не учитываем.
Считая, что все количество теплоты, выделяющееся в предохранителе, идёт на его нагревание, можно написать:
Q1 = Q2 (3)
или, используя выражения (1) и (2), получим
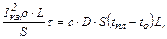
откуда
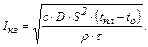 (4)
(4)
Подставим числовые значения величин в (4) и вычислим ток короткого замыкания: 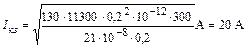 .
.
Ответ: Iкз = 20 A.
Пример 11. Термопара (рис. 8) с сопротивлением r1 = 6 Ом включена в цепь с гальванометром, сопротивление которого r2 = 4 Ом. Чувствительность гальванометра (цена одного деления) Io = 5∙10-2 мкА. Какое минимальное изменение температуры позволяет определить термопара, если её постоянная k = 5∙10-2 мВ/oС?
| Дано: r1 = 6 Ом; r2 = 4 Ом; Iо = 5·10-2 мкА = 5·10-8 А; k = 5·10-2 мВ/ºС = 5·10-5 В/ºС. Найти: ∆tmin. |  Рис. 8 Рис. 8
|
Решение: Минимальное изменение температуры, фиксируемое данным измерительным устройством, соответствует смещению стрелки гальванометра на одно деление.
Электродвижущая сила термопары, согласно принципу её действия, пропорциональна разности температур ∆t спаев:
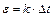 . (1)
. (1)
Согласно закону Ома для замкнутой цепи,
 . (2)
. (2)
При минимальном изменении температуры ток I = Io. Из формул (1) и (2) получим
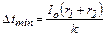 . (3)
. (3)
Таким образом, 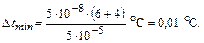
Ответ: ∆tmin = 0,01 oС.