Предмет н.г
Начертательная геометрия является одной из фундаментальных наук, составляющих основу инженерно-технического образования. Она изучает методы изображений пространственных геометрических фигур на плоскости и способы решения по этим изображениям метрических и позиционных задач в пространстве. Начертательная геометрия используется также при конструировании сложных поверхностей технических форм в авиационной, судостроительной и других отраслях транспорта и промышленности. Методы начертательной геометрии позволяют решать многие прикладные задачи специальных инженерных дисциплин.
Методы проецирования
Для отображения точек оригинала на чертеже применяют операцию проецирования. В зависимости от положения проецирующих лучей проецирование может быть либо центральным (коническим), либо параллельным (цилиндрическим). При центральном проецировании все проецирующие лучи исходят из одной точки - центра проецирования, находящегося на определённом расстоянии от плоскости проекций. При параллельном проецировании все проецирующие лучи параллельны между собой.
центр.проец.
Параллельное проецирование. Параллельное проецирование можно рассматривать как частный случай центрального проецирования с бесконечно удаленным центром проекций. При параллельном проецировании все проецирующие лучи параллельны между собой.
Инвариантные св-ва
1. Проекция точки есть точка
2. Проекция прямой есть прямая
3.Если точка К принадлежит прямой а, то и проекция этой точки принадлежит проекции прямой
4. Если точка К делит отрезок АDв отношенииm:nто и проекция этой точки делит в таком же отношении проекцию этого отрезка
|
|
5. Проекция точки пересечения прямых есть точка пересечения проекций этих прямых
6. Проекции параллельных прямых параллельны
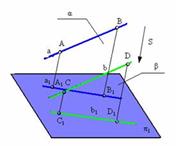
7. Плоский многоугольник в общем случае проецируется в многоугольник с тем же числом вершин.
8. Прямая, параллельная направлению проецирования, проецируется в точку
7 и 8 инвариантные свойства
9. Проекция плоской фигуры, параллельной плоскости проекций, конгруэнтна этой фигуре
Ортогональное проецирование.
ортогональное проецирование - это частный случай параллельного проецирования. При ортогональном проецировании проецирующие лучи перпендикулярны к плоскости проекций.
1. Проекция точки есть точка
2. Проекция прямой есть прямая
3.Если точка К принадлежит прямой а, то и проекция этой точки принадлежит проекции прямой
4. Если точка К делит отрезок АDв отношенииm:nто и проекция этой точки делит в таком же отношении проекцию этого отрезка
5. Проекция точки пересечения прямых есть точка пересечения проекций этих прямых
6. Проекции параллельных прямых параллельны
7. Плоский многоугольник в общем случае проецируется в многоугольник с тем же числом вершин.
8. Прямая, параллельная направлению проецирования, проецируется в точку
9. Проекция плоской фигуры, параллельной плоскости проекций, конгруэнтна этой фигуре
10. Если хотя бы одна сторона прямого угла параллельна плоскости проекций, то на эту плоскость проекций прямой угол проецируется без искажения
| Теорема: |
Если хотя бы одна сторона прямого угла параллельна плоскости проекций, а вторая ей не перпендикулярна, то угол на эту плоскость проецируется в натуральную величину.
|
|
Следствие: если прямоугольная проекция угла, одна сторона которого параллельна плоскости проекций, - прямой угол, то проецируемый угол также прямой.
Система плоскостей проекции. Все пространственные геометрические фигуры могут быть ориентированы относительно декартовой прямоугольной системы координатных осей - системы трех взаимно перпендикулярных координатных плоскостей
Эти координатные плоскости обозначаются: 1. Горизонтальная плоскость проекций - π1;
2. Фронтальная плоскость проекций - π2;
3. Профильная плоскость проекций - π3.
ось абсцисс Х делит горизонтальную плоскость проекций π1 на две части: переднюю полу π1 (оси Х и Y) и заднюю полу π1 (оси Х и - Y).
Ось абсцисс Х делит фронтальную плоскость проекций π2 также на две части: верхнюю полу π2 (оси Х и Z) и нижнюю полу π2 (оси Х и - Z).
Оси ординат Y и аппликат Z делят профильную плоскость проекций π3 на четыре части:
1. Верхнюю переднюю полу π3 (оси Y и Z)
2. Верхнюю заднюю полу π3 (оси –Y и Z)
3. Нижнюю переднюю полу π3 (оси Y и –Z)
4. Нижнюю заднюю полу π3 (оси – Y и –Z)
Эпюра Монжа Для построения плоской модели пространственной геометрической фигуры каждая ее точка проецируется ортогонально на плоскости проекций π1, π2 и π3, которые затем совмещаются в одну плоскость. Полученная таким образом плоская модель пространственной геометрической фигуры называется эпюром Монжа.
Прямая.
Прямая не параллельная ни одной из плоскостей проекций, называется прямой общего положения.
Положение прямой в пространстве необходимо и достаточно определяется двумя точками, ей принадлежащими или точкой и направляющим вектором
|
|
Частное положение прямой
1. Горизонтальная прямая h – горизонталь
Горизонтальная прямая – это прямая, параллельная горизонтальной плоскости проекций π1.
2. Фронтальная прямая f – фронталь
Фронтальная прямая – это прямая параллельная фронтальной плоскости проекций π2.
3. Профильная прямая p (рис. 2.4)
Профильная прямая – это прямая, параллельная профильной плоскости проекций π3
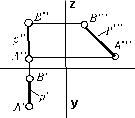
Проецирующие прямые
Прямые перпендикулярные к какой-либо координатной плоскости называются проецирующими прямыми.
Они делятся на горизонтально-проецирующие, фронтально-конкурирующие, профильно-проецирующие.
Проецирующие прямые имеют два важных свойства:
1. они параллельны двум координатным плоскостям
2. на плоскость к которой они перпендикулярны они проецируются в точку
ГОРИЗОНТАЛЬНО - ПРОЕЦИРУЮЩИЕ ПРЯМЫЕ
ФРОНТАЛЬНО - ПРОЕЦИРУЮЩИЕ ПРЯМЫЕ
ПРОФИЛЬНО - ПРОЕЦИРУЮЩИЕ ПРЯМЫЕ
Следы прямой
Следом прямой линии называется точка, в которой прямая пересекается с плоскостью проекций (так как след - точка, принадлежащая одной из плоскостей проекций, то одна из её координат должна быть равна нулю)
Горизонтальный след - М (zM=0)- точка пересечения прямой с горизонтальной плоскостью проекций.
Фронтальный след - N (yN=0) - точка пересечения прямой с фронтальной плоскостью проекций.
Профильный след - Т (xТ=0) - точка пересечения прямой с профильной плоскостью проекций.
Взаимное положение прямых
Две прямые в пространстве могут пересекаться, скрещиваться и могут быть параллельны.
1. Пересекающиеся прямые
Пересекающимися прямыми называются такие прямые, которые имеют одну общую точку.
2. Параллельные прямые
параллельные прямые – прямые, пересекающиеся в несобственной точке (прямые, лежащие в одной плоскости и пересекающиеся в бесконечно удаленной точке).
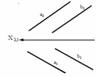
3. Скрещивающиеся прямые
Скрещивающиеся прямые – это прямые, не лежащие в одной плоскости, это прямые не имеющие ни одной общей точки.
Перпендикулярные прямые
Две прямые, пересекающиеся под прямым углом, называются перпендикулярными.
1. Через точку А можно провести только одну перпендикулярную прямую АВ к прямой СD
2. Из точки A можно опустить перпендикуляр на прямую CD
3. Несколько перпендикуляров, проведенных через точки прямой к прямой, никогда между собой не пересекаются