Зачем структурировать информацию?
Давайте сравним четыре сообщения.
Первое:
«Для того чтобы добраться из Москвы до села Васино, нужно сначала долететь на самолёте до города Ивановска. Затем на электричке доехать до Ореховска. Там на пароме переправиться через реку Слоновую в посёлок Ольховка, и оттуда ехать в село Васино на попутной машине».
Второе:
«Как ехать в Васино:
1. На самолёте из Москвы до г. Ивановска.
2. На электричке из г. Ивановска до г. Ореховска.
3. На пароме из г. Ивановска через р. Слоновую в пос. Ольховка.
4. На попутной машине из пос. Ольховка до с. Васино».
Третье:
Четвёртое (рис. 1.7):
Рис. 1.7
Можно считать, что все эти (такие разные по форме!) сообщения содержат одну и ту же информацию. Какие из них проще воспринимать? Очевидно, что человеку «вытащить» полезную информацию из сплошного текста (первое сообщение) сложнее всего. Во втором случае мы сразу видим все этапы поездки и понимаем, в каком порядке они следуют друг за другом. Третье сообщение (таблицу) и четвёртое (схему) можно понять сразу, с первого взгляда. Второй, третий и четвёртый варианты воспринимаются лучше и быстрее первого, потому что в них выделена структура информации, в которой самое главное — этапы поездки в Васино.
Зачем книгу разбивают на главы и разделы, а не пишут сплошной текст? Зачем в тексте выделяют абзацы? Прежде всего для того, чтобы подчеркнуть основные мысли, — каждая глава, раздел, абзац содержат определённую идею. Благодаря особенностям человеческого восприятия, при таком выделении структуры улучшается передача информации от автора к читателю.
При автоматической (компьютерной) обработке правильно выбранная структура данных облегчает доступ к ним, позволяет быстро найти нужные данные.
Средства, облегчающие поиск информации, знакомы вам по работе с книгами. Самый простой (но очень утомительный!) способ найти в книге то, что нужно, — перелистывать страницу за страницей. Однако в большинстве книг есть оглавление, которое позволяет сразу найти нужный раздел, и это значительно ускоряет поиск.
В словарях слова всегда расставлены в алфавитном порядке (представьте себе, что было бы, если бы они были расположены произвольно!). Поэтому, открыв словарь в любом месте, мы можем сразу определить, куда дальше листать страницы для поиска нужного слова — вперёд или назад.
В больших книгах используют указатели (индексы) (рис. 1.8) — списки основных терминов с указанием страниц, на которых они встречаются.
Рис. 1.8
Структурирование — это выделение важных элементов в информационных сообщениях и установление связей между ними.
Цели структурирования для человека — облегчение восприятия и поиска информации, выявление закономерностей. При компьютерной обработке структурирование ускоряет поиск нужных данных.
Знакомые структуры данных
С некоторыми структурами данных вы уже знакомы. Например, на уроках математики вы изучали множество — некоторый набор элементов. Чтобы определить множество, мы должны перечислить все его элементы (например, множество, состоящее из Васи, Пети и Коли) или определить характерный признак, по которому элементы включаются в это множество (например, множество драконов с пятью зелёными хвостами или множество точек, в которых функция принимает положительные значения).
Множество может состоять из конечного числа элементов (множество букв русского алфавита), бесконечного числа элементов (множество натуральных чисел) или вообще быть пустым (множество слонов, живущих на Северном полюсе). Множества, с которыми работает компьютер, не могут быть бесконечными, потому что его память конечна.
В документах множество часто оформляют в виде маркированного списка, например:
• процессор;
• память;
• устройства ввода;
• устройства вывода.
В таком списке порядок элементов не важен, от перестановки элементов множество не меняется (рис. 1.9).
 |
Рис. 1.9
Линейный список состоит из конечного числа элементов, которые должны быть расположены в строго определённом порядке.
В отличие от множества элементы в списке могут повторяться. Список обычно упорядочен (отсортирован) по какому-то правилу, например по алфавиту, по важности, по последовательности действий и т. д. В тексте он часто оформляется как нумерованный список, например:
1) надеть носки;
2) надеть ботинки;
3) выйти из дома.
Переставить местами элементы такого списка нельзя (это будет уже другой список). Список можно задать перечислением элементов, с первого до последнего: (надеть носки, надеть ботинки, выйти из дома), а также представить в виде цепочки связанных элементов (рис. 1.10).
Рис. 1.10
Ещё одна знакомая вам структура — таблица. С помощью таблиц устанавливается связь между несколькими элементами. Например, в табл. 1.2 элементы в каждой строке связаны между собой — это свойства некоторого объекта (человека).
Именно так хранится информация в базах данных: строка таблицы, содержащая информацию об одном объекте, называется записью, а столбец (название свойства) — полем.
Возможен и другой вариант таблицы, когда роли строк и столбцов меняются. В первом столбце записываются названия свойств, а данные в каждом из следующих столбцов описывают свойства какого-то объекта. Например, табл. 1.3 содержит характеристики разных марок автомашин.
Иерархия (дерево)
Линейных списков и таблиц иногда недостаточно для того, чтобы представить все связи между элементами. Например, в некоторой фирме есть директор, ему подчиняются главный инженер и главный бухгалтер, у каждого из них есть свои подчинённые. Если мы захотим нарисовать схему управления этой фирмы, она получится многоуровневой (рис. 1.11, а).
Такая структура, в которой одни элементы «подчиняются» другим, называется иерархией (от древнегреческого fepap%ta — священное правление). В информатике иерархическую структуру называют деревом. Дело в том, что, если перевернуть схему на рис. 1.11 вверх ногами, она становится похожа на дерево (точнее, на куст, см. рис. 1.11, б).
Рис. 1.11
Дерево состоит из узлов и связей между ними (они называются дугами). Самый первый узел, расположенный на верхнем уровне (в него не входит ни одна стрелка-дуга), — это корень дерева. Конечные узлы, из которых не выходит ни одна дуга, называются листьями. Все остальные узлы, кроме корня и листьев, — промежуточные.
Из двух связанных узлов тот, который находится на более высоком уровне, называется родителем, а другой — сыном. Корень — это единственный узел, у которого нет родителя; у листьев нет сыновей.
Используются также понятия предок и потомок. Потомок какого-то узла — это узел, в который можно перейти по стрелкам от узла-предка. Соответственно, предок какого-то узла — это узел, из которого можно перейти по стрелкам в данный узел.
В дереве на рис. 1.12 родитель узла Е — это узел В, а предки узла Е — это узлы А я В, для которых узел Е — потомок. Потомками узла А (корня) являются все остальные узлы.
Рис. 1.12
Типичный пример иерархии — различные классификации (животных, растений, минералов, химических соединений). Например, отряд Хищные делится на два подотряда: Псообразные и Кошкообразные. В каждом из них выделяют несколько семейств (рис. 1.13).
Рис. 1.13
Конечно, на рис. 1.13 показаны не все семейства, остальные обозначены многоточиями.
В текстах иерархию часто представляют в виде многоуровневого списка. Например, оглавление книги о хищниках может выглядеть так:
Глава 1. Псообразные
1.1. Псовые
1.2. Енотовые
1.3. Медвежьи
...
Глава 2. Кошкоообразные
2.1. Кошачьи
2.2. Гиеновые
2.3. Мангустовые
...
Работая с файлами и папками, мы тоже встречаемся с иерархией: классическая файловая система имеет древовидную структуру 1. Вход в папку — это переход на следующий (более низкий) уровень иерархии (рис. 1.14).
1 В современных файловых системах (NTFS, ext3) файл может «принадлежать» нескольким каталогам одновременно. При этом древовидная структура, строго говоря, нарушается.
Рис. 1.14
Алгоритм вычисления арифметического выражения тоже может быть представлен в виде дерева (рис. 1.15).
(а + 3) * 5 - 2 * b
Рис. 1.15
Здесь листья — это числа и переменные, тогда как корень и промежуточные вершины — знаки операций. Вычисления идут «снизу вверх», от листьев — к корню. Показанное дерево можно записать так:
(-(*(+ (а,3),5),*(2,b)))
Самое интересное, что скобки здесь необязательны; если их убрать, то выражение всё равно может быть однозначно вычислено:
* + а35 * 2b
Такая запись, которая называется префиксной (операция записывается перед данными), просматривается с конца. Как только встретится знак операции, эта операция выполняется с двумя значениями, записанными справа. В рассмотренном выражении сначала выполняется умножение:
- * + а 3 5 (2*b)
затем — сложение:
- * (а + 3) 5 (2 * b)
и ещё одно умножение:
- (а + 3) * 5 (2*b)
и наконец, вычитание:
(а + 3) * 5 - (2 * b)
Для получения префиксной записи мы обходили все узлы дерева в порядке «корень — левое поддерево — правое поддерево». Действительно, сначала записана метка корня («-»), затем все метки левого поддерева, а затем — все метки правого поддерева. Для поддеревьев используется тот же порядок обхода. Если же обойти дерево в порядке «левое поддерево — правое поддерево — корень», получается постфиксная форма (операция после данных). Например, рассмотренное выше выражение может быть записано в виде
аЗ+5*2b*-
Для вычисления такого выражения скобки также не нужны, и это очень удобно для автоматических расчётов. Когда программа на языке программирования высокого уровня переводится в машинные коды, часто все выражения записываются в бесскобочной постфиксной форме и именно так и вычисляются. Постфиксная форма для компьютера удобнее, чем префиксная, потому что, когда программа доходит до знака операции, все данные для выполнения этой операции уже готовы.
Графы
Подумайте, как можно структурировать такую информацию:
«От посёлка Васюки три дороги идут в посёлки Солнцево, Грибное и Ягодное. Между Солнцевым и Грибным и между Грибным и Ягодным также есть дороги. Кроме того, есть дорога, которая идет из Грибного в лес и возвращается обратно в Грибное».
Можно, например, нарисовать схему дорог (рис. 1.16, а). На рисунке 1.16, б населённые пункты для краткости обозначены латинскими буквами.
Рис. 1.16
Для исследования таких схем используют графы.
Граф — это набор вершин и связей между ними (рёбер).
Для хранения информации о вершинах и связях графа, соответствующего схеме на рис. 1.16, можно использовать таблицу (матрицу), показанную на рис. 1.17.
Рис. 1.17
Единица на пересечении строки А и столбца В означает, что между вершинами А и В есть связь. Ноль указывает на то, что связи нет. Такая таблица называется матрицей смежности. Она симметрична относительно главной диагонали (серые клетки в таблице).
На пересечении строки С и столбца С стоит единица, которая говорит о том, что в графе есть петля — ребро, которое начинается и заканчивается в одной и той же вершине.
Можно поступить иначе: для каждой вершины перечислить все вершины, с которыми связана данная вершина. В этом случае мы получим список смежности. Для рассмотренного графа список смежности выглядит так:
(А (В, С), В (А, С, D), С (А, В, С, В), D (В, С))
Строго говоря, граф — это математический объект, а не рисунок. Конечно, его можно нарисовать на плоскости (например, как на рис. 1.16, б), но матрица смежности и список смежности не дают никакой информации о том, как именно следует располагать узлы друг относительно друга. Для таблицы на рис. 1.17 возможны, например, варианты, показанные на рис. 1.18.
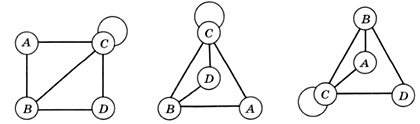
Рис. 1.18
В рассмотренном примере все вершины связаны, т. е. между любой парой вершин существует путь — последовательность рёбер, по которым можно перейти из одного узла в другой. Такой граф называется связным.
Связный граф — это граф, между любыми вершинами которого существует путь.
Теперь представьте себе, что дороги Басюки — Солнцево, Басюки — Грибное и Грибное — Ягодное завалило снегом (или размыло дождём) так, что по ним не пройти и не проехать (рис. 1.19).
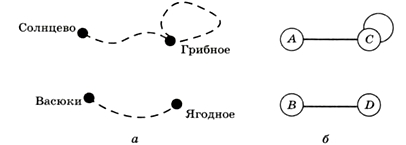
Рис. 1.19
Схему на рис. 1.19, а тоже можно считать графом (она подходит под определение), но в таком графе есть две несвязанные части, каждая из которых — связный граф. Такие части называют компонентами связности.
Вспоминая материал предыдущего пункта, можно сделать вывод, что дерево — это частный случай связного графа. Но у дерева есть одно важное свойство — в нём нет замкнутых путей (циклов). Граф на рис. 1.17 не является деревом, потому что в нём есть циклы: АВСА, BCDB, ABDCA.
Дерево — это связный граф, в котором нет циклов.
Если в первом примере с дорогами нас интересуют ещё и расстояния между поселками, каждой связи нужно сопоставить число (вес) (рис. 1.20).
Рис. 1.20
Такой граф называется взвешенным, поскольку каждое ребро имеет свой вес. Весом может быть не только расстояние, но и, например, стоимость проезда или другая величина.
Как хранить информацию о таком графе? Ответ напрашивается сам собой — нужно в таблицу записывать не 1 или 0, а вес ребра. Если связи между двумя вершинами нет, на бумаге можно оставить ячейку таблицы пустой, а при хранении в памяти компьютера записывать в неё условный код, например -1. Такая таблица называется весовой матрицей, потому что содержит веса рёбер. В данном случае она выглядит, как показано на рис. 1.21.
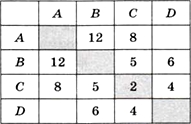
Рис. 1.21
Так же как и матрица смежности, весовая матрица симметрична относительно главной диагонали. Нижняя ячейка в столбце А и верхняя в столбце D говорят о том, что между вершинами А и D нет ребра.
Если в графе немного вершин, весовая матрица позволяет легко определить наилучший маршрут из одной вершины в другую простым перебором вариантов. Рассмотрим граф, заданный весовой матрицей на рис. 1.22 (числа определяют стоимость поездки между соседними пунктами).
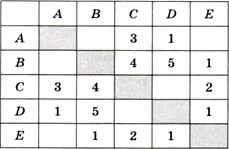
Рис. 1.22
Найдём наилучший путь из А в В — такой, при котором общая стоимость поездки минимальная. Сначала видим, что из пункта А напрямую в В ехать нельзя, а можно ехать только в С и D. Изобразим это на схеме (рис. 1.23).
Рис. 1.23
Числа около рёбер показывают стоимость поездки по этому участку, а индексы у названий вершин показывают общую стоимость проезда в данную вершину из вершины А.
Теперь разберём варианты дальнейшего движения из вершины С (вершину А уже не нужно рассматривать, так как мы из неё пришли) (рис. 1.24).
Рис. 1.24
Видим, что из С сразу можно попасть в В, стоимость проезда в этом случае равна 7. Но, возможно, это не самый лучший вариант, и нужно проверить ещё путь через вершину Е. Действительно, оказывается, что можно сократить стоимость до 6 (рис. 1.25).
Рис. 1.25
Исследовать дальше маршрут, содержащий цепочку ACED, нет смысла, потому что его стоимость явно будет больше 6. Аналогично строим вторую часть схемы (вы догадались, что схема представляет собой дерево!) (рис. 1.26).
Рис. 1.26
Таким образом, оптимальный (наилучший) маршрут — ADEB, его стоимость — 3. Маршрут ADEC, не дошедший до вершины В, далее проверять не нужно, он не улучшит результат.
Конечно, для более сложных графов метод перебора работает очень долго, поэтому используются более совершенные (но более сложные) методы, о которых мы поговорим в 11 классе.
Наверное, вы заметили, что при изображении деревьев, которые описывают иерархию (подчинение), мы ставили стрелки от верхних уровней к нижним. Это означает, что для каждого ребра указывается направление, и двигаться можно только по стрелкам, но не наоборот. Такой граф называется ориентированным (или коротко орграфом). Он может служить, например, моделью системы дорог с односторонним движением. Матрица смежности и весовая матрица для орграфа уже не обязательно будут симметричными.
На схеме на рис. 1.27 всего две дороги с двусторонним движением, по остальным можно ехать только в одну сторону.
Рёбра в орграфе называют дугами. Дуга, в отличие от ребра, имеет начало и конец.
Рис. 1.27
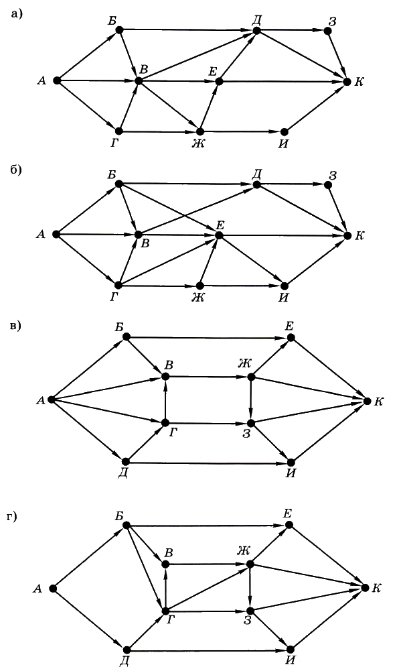
Рассмотрим следующую задачу: определить количество возможных путей из вершины А в вершину К для ориентированного графа, показанного на рис. 1.28.
Рис. 1.28
Так как граф ориентированный, переходить в другую вершину можно только по стрелкам. Будем двигаться по стрелкам от начальной вершины А. Около каждой вершины запишем количество возможных путей из вершины А в эту вершину. Найдём все вершины, в которые можно попасть только из А: это вершины Б и Г, записываем около них количество путей 1 (рис. 1.29).
Рис. 1.29
Теперь ищем вершины, в которые можно попасть только из уже отмеченных вершин. Например, в вершину В есть один путь из А напрямую, а также по одному пути через Б и Г (так как эти вершины отмечены числом 1). Общее количество путей из А в В вычисляется как сумма отметок предыдущих вершин. В данном случае получаем всего три маршрута из А в В. В вершину Ж можно попасть только из Г, поэтому число путей в Г и Ж совпадает (рис. 1.30).
Рис. 1.30
В вершину Д идёт один путь через В и три пути через В, поэтому общее число путей — четыре. Аналогично получаем четыре пути в вершину Е: три пути через В и один — через Ж (рис. 1.31).
Рис. 1.31
Далее находим один путь из А в If (только через Ж) и четыре пути из А в 3 (все через Д). В конечную вершину К можно попасть через вершины Д (четыре пути), 3 (четыре пути), Е (четыре пути) и И (один путь), таким образом, общее количество различных путей равно 13 (рис. 1.32).
Рис. 1.32
Вопросы и задания
1. Что такое структурирование информации? Зачем оно нужно?
2. Что такое алфавитный порядок? Как поступают, если начальные символы слов совпали?
3. Расскажите, как используются оглавление, словарь и индекс для быстрого поиска нужной информации. Чем эти средства отличаются друг от друга?
4. Какими способами можно задать множество? Что такое пустое множество?
5. Приведите примеры множеств.
6. Чем отличаются множество и линейный список?
7. Что такое матрица?
8. Как можно записать табличные данные в виде списка?
9. Что такое иерархия? Приведите примеры.
10. Вспомните известные вам классификации, которые вы изучали на других предметах.
11. Как называется иерархическая структура в информатике?
12. Что такое корень, лист, родитель, сын, предок, потомок в структуре «дерево»?
13. В дереве 4 потомка, и все они являются листьями. Нарисуйте это дерево. Сколько в нём вершин?
14. В чём разница между понятиями «ребро» и «дуга»?
15. В чём различие понятий «дерево», «граф»?
16. Какой граф называется связным?
17. Что такое компонента связности?
18. Что такое петля? Как по матрице смежности определить, есть ли петли в графе?
19. Что такое орграф? Когда для представления данных используются орграфы? Приведите примеры.
20. Выберите наиболее подходящий способ структурирования информации для хранения:
а) данных о крупнейших озерах мира;
б) рецепта приготовления шашлыка;
в) схемы железных дорог;
г) схемы размещения файлов на флэш-диске.
Подготовьте сообщение
а) «Как вычисляются арифметические выражения?»
б) «Постфиксная и инфиксная формы записи выражений»
в) «Графы в практических задачах»
г) «Диаграммы связей (mind maps)»
д) «Системы классификации книг (ДКД, УДК)»
Задачи
1. Определите выражения, соответствующие каждому из деревьев, в «нормальном» виде со скобками (эту форму называют инфиксной — операция записывается между данными). Постройте для каждого из них постфиксную форму.
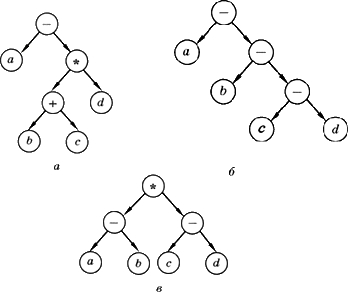
2. Постройте деревья, соответствующие следующим арифметическим выражениям. Запишите эти выражения в префиксной и постфиксной формах:
а) (a+b)*(c+2*d)
б) (2*a-3*d)*c+2*b
в) (a+b+2*c)*d
г) 3*a-(2*b+c)*d
3. Вычислите выражения, записанные в постфиксной форме:
а) 12 6 + 7 3 - 1 - * 12 +
б) 12 10 - 5 7 + * 7 - 2 *
в) 5 6 7 8 9 + - + -
г) 5 4 3 2 1 - - - -
Запишите каждое из них в инфиксной и в префиксной формах и постройте соответствующее дерево. Единственно ли такое дерево? В этом дереве назовите корень, листья и промежуточные вершины.
4. Нарисуйте граф, в котором 5 вершин и три компоненты связности. Постройте его матрицу смежности.
5. Структурируйте следующую информацию разными способами: «Между посёлками Верхний и Нижний есть просёлочная дорога длиной 10 км. Село Сергеево соединяется двумя асфальтовыми шоссе с Нижним (22 км) и Верхним (16 км). В село Солнечное можно доехать только из Сергеева по грунтовой дороге (5 км)». Можно ли сказать точно, как расположены эти пункты?
6. Для графа, полученного в предыдущей задаче, постройте матрицу смежности, список смежности, весовую матрицу. Является ли этот граф деревом?
7. Постройте матрицы смежности и весовые матрицы графов:
8. Постройте графы, соответствующие матрицам смежности.
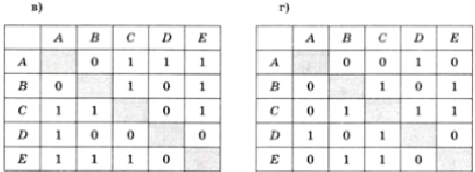
9. Постройте графы, соответствующие весовым матрицам.
10. Стоимость перевозок между пунктами, которые для краткости обозначены буквами А, В, С, D и Е, задаётся таблицей (весовой матрицей графа). Нужно перевезти груз из пункта А в пункт В. Для каждого из четырёх вариантов определите оптимальный маршрут и полную стоимость перевозки.
11. Постройте орграфы, соответствующие весовым матрицам.
Для каждого из орграфов найдите количество различных маршрутов из вершины А во все остальные вершины.
