Комбинаторика
Основная задача комбинаторики – пересчет и перечисление элементов в конечных множествах. Первая задача состоит в вычислении числа элементов, обладающих заданным свойством или набором свойств. Вторая – состоит в выделении всех интересующих нас элементов. Если на исходном множестве определена некоторая целевая функция, экстремум которой необходимо найти, то решение задачи оптимизации в сильном смысле – это отыскание всех элементов, на которых достигается экстремум, а в слабом смысле – это нахождениепроизвольного элемента, доставляющего экстремум целевой функции.
При решении задач оптимизации обычно предполагается наличие методов перечисления элементов исходного множества, а для оценки эффективности методов перечисления или оптимизации часто целесообразно решать задачу пересчета элементов в исходном множестве или в некоторых его подмножествах.
Комбинаторные схемы
Пусть задано конечное множество Х, такое, что  . Тогда объект
. Тогда объект  из Х может быть выбран n способами. Пусть множества Хi, где
из Х может быть выбран n способами. Пусть множества Хi, где  таковы, что
таковы, что  и
и  , если i¹j. Тогда выполняется равенство
, если i¹j. Тогда выполняется равенство

Этот факт в комбинаторике называется правилом суммы, которое утверждает, что так как объект  можно выбрать ni способами из Х (
можно выбрать ni способами из Х ( ÎХiÌХ), то выбор из Х либо
ÎХiÌХ), то выбор из Х либо  , либо
, либо  , либо
, либо  можно осуществить n1+n2+…+nk способами.
можно осуществить n1+n2+…+nk способами.
В другом случае, если мы будем осуществлять выбор упорядоченного набора (кортежа) <  ,
,  ,…,
,…,  >, где
>, где  ÎXi, то очевидно, что такой набор можно осуществить
ÎXi, то очевидно, что такой набор можно осуществить 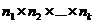 способами. Это следует из равенства
способами. Это следует из равенства
 .
.
Это так называемое правило произведения, которое можно проиллюстрировать задачей.
Задача 2.1. Найти число возможных десятичных четырехзначных чисел (не начинающихся, естественно, с нуля).
Решение. Для первого символа (слева)  , для остальных символов
, для остальных символов 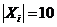 ,
, 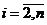 . Следовательно, число всех возможных комбинаций <a1, a2, a3, a4>, где a1¹0, равно
. Следовательно, число всех возможных комбинаций <a1, a2, a3, a4>, где a1¹0, равно  .
.
Схемы без повторений
Пусть мы имеем конечное множество Х={  ,
,  ,…,
,…,  }, тогда набор элементов
}, тогда набор элементов  ,…,
,…,  называется выборкой объема r из n элементов или, иначе, (n,r)-выборкой. Выборка называется упорядоченной, если порядок следования элементов в ней фиксирован, и две выборки, различающиеся лишь порядком следования элементов, считаются различными.
называется выборкой объема r из n элементов или, иначе, (n,r)-выборкой. Выборка называется упорядоченной, если порядок следования элементов в ней фиксирован, и две выборки, различающиеся лишь порядком следования элементов, считаются различными.
Число возможных различных упорядоченных (n,r)-выборок с такими элементами, что  ¹
¹  , если
, если  и j¹k равно числу различных r-векторов <
и j¹k равно числу различных r-векторов <  ,…,
,…,  >, которые могут быть построены на Х={
>, которые могут быть построены на Х={  ,…,
,…,  }. Это число называется числом размещений из n элементов по r и обозначается
}. Это число называется числом размещений из n элементов по r и обозначается 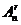 . Докажем, что
. Докажем, что
 , (2.1)
, (2.1)
где  и называется k-факториал.
и называется k-факториал.
Очевидно, что для выбора  у нас есть n возможностей. После выбора элемента
у нас есть n возможностей. После выбора элемента  и удаления его из Х, для выбора
и удаления его из Х, для выбора  остается (n-1) возможность и т.д. Тогда при выборе элемента
остается (n-1) возможность и т.д. Тогда при выборе элемента  имеется [n-(r-1)] возможностей и в итоге имеем
имеется [n-(r-1)] возможностей и в итоге имеем

 .
.
Если рассмотреть множество всех различных n-векторов <xi1, xi2,…,xin>, которые можно построить на Х, то каждая такая выборка называется перестановкой, поскольку различаются они только расположением элементов. Перестановки обозначаются Рn. Докажем, что
 . (2.2)
. (2.2)
Для этого выберем первый элемент  ÎХ и рассмотрим все перестановки, в которых
ÎХ и рассмотрим все перестановки, в которых  имеет номер 1. Число таких перестановок с очевидностью равно Рn-1. Обозначим через М множество всех перестановок множества Х, а через Мi – множество всех перестановок, в которых
имеет номер 1. Число таких перестановок с очевидностью равно Рn-1. Обозначим через М множество всех перестановок множества Х, а через Мi – множество всех перестановок, в которых  имеет номер i. Тогда
имеет номер i. Тогда
М=М1ÈМ2È…ÈМn,
где  , если i¹j, поскольку элементы множеств Мi и Мj различаются положением элемента
, если i¹j, поскольку элементы множеств Мi и Мj различаются положением элемента  .
.
Используя предыдущий вывод, что |Мi|=Рn-1, 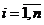 , можно записать
, можно записать
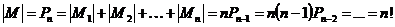 .
.
Используя (2.1) для размещений  , соответствующих упорядоченным выборкам (n,n), можно записать:
, соответствующих упорядоченным выборкам (n,n), можно записать:

С другой стороны, эти выборки соответствуют n-перестановкам, и из (2.2) следует, что

откуда мы должны положить 0!=1.
Рассмотрим теперь неупорядоченные выборки {  ,…,
,…,  } r-элементов из Х, которые считаются различными, если они отличаются хоть одним элементом. Таким образом, каждая такая (n,r)-выборка есть подмножество мощности r множества Х. Задача состоит в подсчете числа разных r-элементных подмножеств из n-элементного множества Х. Каждое такое подмножество называется сочетанием из n-элементов по r, а их общее число обозначается
} r-элементов из Х, которые считаются различными, если они отличаются хоть одним элементом. Таким образом, каждая такая (n,r)-выборка есть подмножество мощности r множества Х. Задача состоит в подсчете числа разных r-элементных подмножеств из n-элементного множества Х. Каждое такое подмножество называется сочетанием из n-элементов по r, а их общее число обозначается  . Покажем, что
. Покажем, что
 . (2.3)
. (2.3)
Для этого можем заметить, что каждой выборке (сочетанию) {  ,…,
,…,  } соответствует r! упорядоченных выборок (размещений) <
} соответствует r! упорядоченных выборок (размещений) <  ,…,
,…,  > за счет перестановок r элементов, то есть
> за счет перестановок r элементов, то есть
 ,
,
откуда следует после применения (2.1), что
 .
.
Задача 2.2. Сколькими способами можно упорядочить множество {1,2,…,2n-1, 2n} так, чтобы каждое четное число имело четный номер?
Решение. Задача состоит в расположении нечетных чисел (их всего n) по нечетным, а четных (их тоже n) - по четным местам.
Очевидно, что первая подзадача имеет решение n!. Но точно так для каждой комбинации нечетных чисел имеется n! перестановок четных чисел по четным местам. В итоге общее число комбинаций равно n! *n!= (n!)2.
Задача 2.3. Сколько существует способов упорядочить множество {1,2,…,n} так, чтобы числа 1,2,3 стояли рядом и в порядке возрастания?
Решение. Число 1 (а 2 и 3 должны стоять рядом справа) можно записать на 1-е, 2-е,…,(n-2)-е место, то есть всего (n-2) возможности. В каждом случае оставшиеся (n-3) чисел могут быть расставлены (n-3)! способами. Таким образом, число интересующих нас комбинаций равно (n-2)(n-3)!.
Задача 2.4. При повороте листа бумаги с цифрами на 180°цифры 0,1,8 не изменяются, 6 и 9 переходят друг в друга, а остальные теряют смысл. Сколько существует семизначных чисел, не содержащих одинаковых цифр и не изменяющихся при повороте листа?
Решение. Очевидно, что 4-е место (центральное) в числе могут занимать 0,1 или 8. Это составляет 3 возможности. Для каждой из этих возможностей для тройки чисел справа (или слева) от центральной цифры нужно из четырех оставшихся цифр составить комбинацию из трех цифр. Всего таких комбинаций 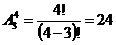 , а следовательно, общее число возможных искомых семизначных чисел равно N=3*24=72.
, а следовательно, общее число возможных искомых семизначных чисел равно N=3*24=72.
Задача 2.5. На плоскости заданы n точек, все попарно соединенные линиями, называемые ребрами. Сколько всего ребер?
Решение. Пусть каждой точке соответствует элемент множества X={  ,…,
,…,  }. Тогда каждое ребро определяет подмножество X, состоящее из двух элементов, и задача состоит в отыскании числа всех 2-х элементных подмножеств в X, которое равно числу сочетаний:
}. Тогда каждое ребро определяет подмножество X, состоящее из двух элементов, и задача состоит в отыскании числа всех 2-х элементных подмножеств в X, которое равно числу сочетаний:


Рис.2.1. Схема одного из кратчайших путей на сетке
Задача 2.6. На прямоугольной сетке m´n (рис. 2.1) найти число различных кратчайших путей, соединяющих точки (0,0) и (m,n).
Решение. Любой кратчайший путь из (0,0) в (m,n) состоит из m+n отрезков, среди которых m горизонтальных и n вертикальных. Разные пути различаются лишь порядком чередования горизонтальных и вертикальных отрезков. Поэтому их число равно числу способов выбора мест n вертикальных отрезков на общем числе шагов m+n, т.е. числу сочетаний  Очевидно, этот же результат будет получен, если размещать m горизонтальных отрезков на n+m шагах, а, следовательно,
Очевидно, этот же результат будет получен, если размещать m горизонтальных отрезков на n+m шагах, а, следовательно,
 . (2.4)
. (2.4)
Применяя, использованный в задаче 2.5 так называемый метод траекторий, можно доказать тождество
 . (2.5)
. (2.5)
Действительно, из рисунка 2.1 следует, что общее число кратчайших путей из  в
в  равно сумме путей, ведущих из
равно сумме путей, ведущих из  в точку А1 с координатами
в точку А1 с координатами  в точку A2 с координатами
в точку A2 с координатами  , т.е.:
, т.е.:
 .
.
Переобозначив m+n=r, получим формулу (2.5):
 .
.
Точно так же можно доказать, что
 . (2.6)
. (2.6)
Для этого на рисунке 2.1 положим, что m=n и обратим внимание, что в соответствии с (2.4) общее число кратчайших путей из (0,0) в (n,n) равно  С другой стороны, каждый из этих путей проходит через одну и только одну из точек Ak (k,n-k), лежащих на диагонали, соединяющей точки (0,n) и (n,0). Тогда число различных путей из (0,0) в (n,n), проходящих через Ak (k,n-k), равно произведению числа путей, ведущих в Ak и из Ak в (n,n), т.е.
С другой стороны, каждый из этих путей проходит через одну и только одну из точек Ak (k,n-k), лежащих на диагонали, соединяющей точки (0,n) и (n,0). Тогда число различных путей из (0,0) в (n,n), проходящих через Ak (k,n-k), равно произведению числа путей, ведущих в Ak и из Ak в (n,n), т.е.
 . (2.7)
. (2.7)
Суммируя по всем точкам k=0,1,…,n, получим выражение, стоящее справа в (2.6).
Числа  называются также биноминальными коэффициентами, что связано с формулой бинома Ньютона:
называются также биноминальными коэффициентами, что связано с формулой бинома Ньютона:
 (2.8)
(2.8)
Докажем эту формулу, используя представление:
 .
.
Перемножая последовательно (a+b) n раз, получим сумму 2nслагаемых вида  где
где 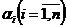 равно a или b. Разобьем слагаемые на n+1 группу B0,B1,B2,…,Bn, отнеся к Bk все те произведения, в которых b встречается множителем k раз, а a - (n-k) раз. Число произведений в Bk равно числу способов выбора k мест из возможных n мест, т.е. равно
равно a или b. Разобьем слагаемые на n+1 группу B0,B1,B2,…,Bn, отнеся к Bk все те произведения, в которых b встречается множителем k раз, а a - (n-k) раз. Число произведений в Bk равно числу способов выбора k мест из возможных n мест, т.е. равно  , а каждое слагаемое в
, а каждое слагаемое в  равно an-kbk .. Поэтому
равно an-kbk .. Поэтому
 .
.
Схемы с повторениями
Поставим такой вопрос: сколькими способами можно разложить множество A={a1,a2,…,an}на m подмножеств 

 ,
,
таких, что
 ?
?
Описанные разбиения можно получить так: возьмем произвольно k1-элементное подмножество B1ÌA (выбор можно осуществить  способами), из оставшихся n-k1 элементов выберем k2 -элементное подмножество B2ÌA\B1 (выбор можно осуществить
способами), из оставшихся n-k1 элементов выберем k2 -элементное подмножество B2ÌA\B1 (выбор можно осуществить 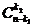 способами) и т.д. Тогда по правилу умножения общее число способов равно:
способами) и т.д. Тогда по правилу умножения общее число способов равно:

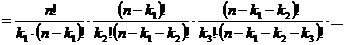

Полученные числа, равные числу перестановок с повторениями
 , (2.9)
, (2.9)
называются полиномиальными коэффициентами, так как они связаны с полиномиальной формулой:

 (2.10)
(2.10)
Перемножив последовательно a1+…+am n раз, получим  слагаемых вида
слагаемых вида  , где каждый множитель равен
, где каждый множитель равен  , или
, или  , …или
, …или  . Пусть B(r1,r2,…,rk) - совокупность всех тех слагаемых, где a1 встречается r1 раз, a2 - r2 раз,…, ak - rk раз, причем r1+r2+…+rk=n. Число таких слагаемых равно числу способов представления множества из n элементов k подмножествами, т.е. используя (2.9)
. Пусть B(r1,r2,…,rk) - совокупность всех тех слагаемых, где a1 встречается r1 раз, a2 - r2 раз,…, ak - rk раз, причем r1+r2+…+rk=n. Число таких слагаемых равно числу способов представления множества из n элементов k подмножествами, т.е. используя (2.9)
B(r1,r2,…,rk)=Cn(r1,r2,…,rk),
а, следовательно, справедливо соотношение (2.10). При k=2, очевидно, получим форму бинома Ньютона.
Еще одна комбинаторная интерпретация коэффициентов (2.9) может быть дана, если для множества n букв, из которых k1 – букв a1, k2 – букв a2,…,km – букв am , k1+k2+…+km=n. Определим число различных слов длины n. Перенумеровав места, на которых стоят буквы номерами {1,2,…,n}, мы каждое слово определим множествами B1(номера мест, где стоит буква a1),B2(номера мест, где стоит a2),…,Bm(номера мест, где стоит буква am). Таким образом, число различных слов равно числу способов, которыми можно представить множество A={1,2,…,n} в виде 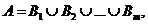 т.е.
т.е.  .
.
Если рассмотреть множество элементов A={a1,…,am}, то можно поставить вопрос о вычислении числа групп (сочетаний) Bk={b1,…,bn}, где bi, 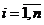 может быть равно одному из aj,
может быть равно одному из aj, 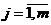 .
.
Например, если A={  } и n=2, то имеем сочетания с повторениями:
} и n=2, то имеем сочетания с повторениями:
 (2.11)
(2.11)
Число различных сочетаний из m элементов по n с повторениями равно
 . (2.12)
. (2.12)
Для доказательства этой формулы укажем, сколько элементов  из A входит в сочетание. Поставим в соответствие каждому сочетанию последовательность нулей и единиц, составленную по правилу: напишем подряд столько единиц, сколько элементов
из A входит в сочетание. Поставим в соответствие каждому сочетанию последовательность нулей и единиц, составленную по правилу: напишем подряд столько единиц, сколько элементов  входит в сочетание, далее поставим нуль и после этого напишем столько единиц, сколько элементов
входит в сочетание, далее поставим нуль и после этого напишем столько единиц, сколько элементов  в сочетании, и т.д. Например, сочетаниям (2.11) соответствуют последовательности:
в сочетании, и т.д. Например, сочетаниям (2.11) соответствуют последовательности:
1100, 1010, 1001, 0110, 0101, 0011.
Таким образом, каждому сочетанию из m по n однозначно соответствует последовательность n единиц и m-1 нулей. Поэтому число сочетаний из m по n с повторениями равно
 .
.
Задача 2.7. Найти число возможных размещений n одинаковых элементов в m урнах.
Решение. Рассмотрим одно из возможных размещений элементов в урнах следующим способом (рис. 2.2): поместим в урну столько единиц, сколько там элементов, расположив между урнами по нулю. Тогда «слово», составленное из единиц в урнах и нулей между ними, будет содержать m+n-1 символ, из которых n единиц и (m-1) нулей. Следовательно, общее число различных размещений равно
 |
 .
.
Рис.2.2. Распределение элементов по урнам так, чтобы 
Задача 2.8. Найти число распределений m+n+s различных элементов на 3 группы по m,n и s элементам каждая.
Решение. Очевидно, что требуется разбить исходное множество A={a1,…,am+n+s} на три подмножества ½A1½=m,½A2½=n,½A3½=s. Используя формулу (2.9), можно записать:

Задача 2.9. Сколько целых неотрицательных корней имеет уравнение: x1+x2+…+xm=n?
Решение. Очевидно, что каждое  ,
,  может принимать значения 0,1,…,n и их сумма должна быть равна n. Тогда задача состоит в отыскании числа сочетаний из m элементов (по числу переменных) по n (общее число элементов), т.е. по формуле (2,12):
может принимать значения 0,1,…,n и их сумма должна быть равна n. Тогда задача состоит в отыскании числа сочетаний из m элементов (по числу переменных) по n (общее число элементов), т.е. по формуле (2,12):
 .
.
Задача 2.10. Сколько целых положительных решений имеет неравенство (m£n) 
Решение. Если произвести замену с использованием тривиального решения xi=1, i=1,m, xi=1+yi, то исходное неравенство приобретает вид y1+y2+…+ym£n-m. Тогда для каждого k=1,2,…,n-m число решений уравнения y1+y2+…+ym=k равно в соответствии с решениями задачи 9 равно  , а общее число решений исходного неравенства равно:
, а общее число решений исходного неравенства равно:

Рассмотрим теперь выборки из n по r, в которых элементы упорядочены и допускаются повторения элементов. Это так называемые (n,r)-размещения с повторениями. Так, для множества X={1,2,3,} такими (3,2)-размещениями будут:
<1,1>,<2,2>,<3,3>,<1,2>,<2,1>,<1,3>,<3,1>,<2,3>,<3,2>.
Покажем, что число таких размещений  равно:
равно:
 . (2.13)
. (2.13)
Действительно, при выборе первого элемента в выборке у нас имеется n возможностей, при выборе второго тоже – n и т.д., всего r раз. Таким образом, по правилу умножения получим:

Формула включений и исключений
Если X1,X2,…,Xn некоторые подмножества множества X, причем в общем случае  , то справедлива формула (1.47), которая в комбинаторике называется формулой включений и исключений:
, то справедлива формула (1.47), которая в комбинаторике называется формулой включений и исключений:
|X1È…ÈXn|=(|X1|+…+|Xn|)-(|X1ÇX2|+|X1ÇX3|+…+|Xn-1ÇXn|)+
+(|X1ÇX2ÇX3|+…+|Xn-2ÇXn-1ÇXn|)-…+(-1)n+1|X1Ç…ÇXn|. (2.14)
Следствием этой формулы является равенство:
|X\(X1È…ÈXn)|=|X|-(|X1|+…+|Xn|)+(|X1ÇX2|+…+|Xn-1ÇXn|)-+
+(-1)n|X1Ç…ÇXn|. (2.15)
Действительно,
[X\(X1È…ÈXn)]È(X1È…ÈXn)=X,
[X\(X1È…ÈXn)]Ç(X1È…ÈXn)=Æ,
откуда
|X\(X1È…ÈXn)|+|X1È…ÈXn|=|X|,
а, следовательно,
|X\(X1È…ÈXn)|=|X|-|X1È…ÈXn|. (2.16)
Для получения (2.15) остается только подставить (2.14) в (2.16).
Более распространенная форма записи формулы включений и исключений может быть получена при рассмотрении конечного множества X, такого что |X|=n и заданных свойств a1,…,ak, которыми элементы X могут обладать или не обладать.
Обозначим:  – множество элементов в Х, обладающих свойством
– множество элементов в Х, обладающих свойством 
 - количество элементов в
- количество элементов в  , обладающих одновременно свойствами
, обладающих одновременно свойствами  ;
;  - количество элементов в
- количество элементов в  , не обладающих ни одним из свойств
, не обладающих ни одним из свойств  . Тогда по формуле (2.15) получаем
. Тогда по формуле (2.15) получаем
 , (2.17)
, (2.17)
где

Задача 2.11. Пусть Х={0,1,...,10};  : «
: « – чётные»;
– чётные»;  : «
: «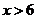 »,
», 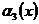 : «
: « ». Найти количество
». Найти количество  элементов в
элементов в  , не обладающих свойствами
, не обладающих свойствами  .
.
Решение. Используя формулу (2.15) и (2.17) получаем  , в следствии того, что
, в следствии того, что 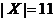 ,
,  ,
,  ,
, 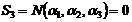 . Очевидно, что этим единственным элементом в
. Очевидно, что этим единственным элементом в  является число 1.
является число 1.
Задача 2.12. (Задача о беспорядках). Имеется n различных предметов 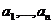 и столько же различных ячеек
и столько же различных ячеек  . Сколькими способами можно разложить предметы по ячейкам так, чтобы никакой предмет
. Сколькими способами можно разложить предметы по ячейкам так, чтобы никакой предмет  не попал в ячейку
не попал в ячейку  ?
?
Решение. Роль исходного множества  выполнит множество всевозможных распределений по ячейкам. Число таких множеств равно числу перестановок
выполнит множество всевозможных распределений по ячейкам. Число таких множеств равно числу перестановок 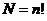 . Введём свойства ai: «
. Введём свойства ai: « находится в ячейке
находится в ячейке  »,
», 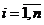 . Число
. Число  расположений, при которых
расположений, при которых  находится в ячейке
находится в ячейке  ,
, 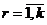 равно
равно  . Тогда
. Тогда

Используя формулу включений и исключений, получаем число  распределений, при которых ни одно из свойств не выполняется, и оно равно:
распределений, при которых ни одно из свойств не выполняется, и оно равно: