ГЕНЕРАЛЬНАЯ СОВОКУПНОСТЬ БЕЗ ПОВТОРЕНИИ И ВЫБОРКИ БЕЗ ПОВТОРЕНИИ.

III. НАУКА О ПОДСЧЕТЕ ЧИСЛА КОМБИНАЦИИ — КОМБИНАТОРИКА.

 

Комбинаторикой называется область математики, в которой изучаются вопросы о том, сколько различных комбинаций, подчиненных тем или иным условиям, можно составить из элементов, принадлежащих заданному множеству. Иногда ком­бинаторику рассматривают как введение в теорию вероятностей, поскольку методы комбинаторики очень помогают в теории ве­роятностей осуществить подсчет числа возможных исходов и числа благоприятных исходов в разных конкретных случаях.

В теории вероятностей принято говорить не о комбинациях, а о выборках. Поэтому мы будем придерживаться термина «выборка».

В комбинаторике рассматриваются виды выборок — пере­становки, размещения, сочетания.

 

1. ОБЩИЕ ПРАВИЛА КОМБИНАТОРИКИ

 

Рассмотрим два общих правила, с помощью которых ре­шается большинство задач комбинаторики,— правило суммы и правило произведения.

Допустим, в ящике имеется п разноцветных шариков. Про­извольным образом вынимаем один шарик. Сколькими способами можно это сделать? Конечно, п способами. Теперь эти п

шариков распределим по двум ящикам: в первом т шариков, во втором k. Произвольно из какого-нибудь ящика вынимаем один шарик. Сколькими разными способами можно это сделать? Из первого ящика шарик можно вынуть т разными спосо­бами, из второго — k разными способами. Всего способами

n = m + k. (3.1)

Если некоторый объект А можно выбрать m способами, а объект В — k способами (не такими, как А), то объект «либо А, либо В» можно выбрать m+k способами.

Это так называемое правило суммы.

Перейдем к правилу произведения. Рассмотрим следующую задачу:

Задача. Сколько можно записать двузначных чисел в де­сятичной системе счисления?

Поскольку число двузначное, число десятков может прини­мать одно из девяти значений: 1, 2, 3, 4, 5, 6, 7, 8, 9. Число еди­ниц может принимать те же значения и может, кроме того, быть равным нулю.

Если цифра десятков 1, цифра единиц может быть 0,1, 2,.... 9 — всего 10 значений. Если цифра десятков 2, то вновь цифра единиц может быть равна 0, 1, 2,..., 9. Всего получаем 90 дву­значных чисел.

Обобщим полученный результат. Пусть данное множество из n = m+k элементов разбито на два подмножества, состоящие соответственно из m и k элементов. Пусть из подмножества, со­держащего m элементов, выбирается один элемент и независимо из подмножества, содержащего k элементов, выбирается один элемент. Спрашивается: сколько различных пар элементов при этом образуется?

Ответ на поставленный вопрос дает таблица:

 

a₁b₁; a₁b₂;…; a₁b_k;

m строк

a₂b₁; a₂b₂;…; a₂b_k;

………………….

a_mb₁; a_mb₂;…; a_mb_k;

 

k пар в каждой строке.

 

Таким образом, если общее число всевозможных пар обоз­начим N, то

N = mk.(3.2)

Сформулируем теперь правило произведений:

Если объект А можно выбрать m способами, а после каждого такого выбора другой объект В можно выбрать (независимо от выбора объекта A) k способами, то пары объектов А и В можно выбрать mk способами.

 

ГЕНЕРАЛЬНАЯ СОВОКУПНОСТЬ БЕЗ ПОВТОРЕНИИ И ВЫБОРКИ БЕЗ ПОВТОРЕНИИ.

 

Генеральная совокупность без повторений — это набор неко­торого конечного числа различных элементов: а₁, а₂, а₃,..., а_n.

Наглядному представлению такой генеральной совокупнос­ти может послужить набор из п разноцветных квадратов.

Выборкой объема т (т 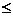п) будем называть произвольную группу из т элементов данной генеральной совокупности. На­глядному представлению такой выборки может служить пест­рая лента, построенная из m квадратов различной окраски.

Каким минимальным признаком может отличиться одна выборка объема т от другой выборки такого же объема? Это равносильно вопросу: каким минимальным признаком могут отличаться узоры двух пестрых лент, построенных из одина­кового количества квадратов?

Иной окраской, по крайней мере, одного квадрата

или порядком расположения квадратов в линейном строю.

Таким образом, минимальным признаком, отличающим од­ну выборку объема т от другой выборки такого же объема, может быть:

их различие, по крайней мере, одним элементом (а) или их различие порядком расположения элементов. (б)

Назовем такие выборки размещениями без повторений из п элементов по т.

Можно построить такой наглядный граф наших рассуж­дений:

 

когда одна от другой отличаются, по крайней мере, одним элементом или порядком расположения элементов

 

Отсюда следует определение понятия:

Размещениями без повторений из п элементов по m назы­ваются такие выборки, которые, имея по m элементов, выбран­ных из числа данных п элементов генеральной совокупности без повторений, отличаются одна от другой либо составом элементов, либо порядком их расположения.

Характерный пример размещений без повторений — вся со­вокупность трехзначных номеров, в каждом из которых нет пов­торения цифр.

Число размещений из п элементов по m договоримся обо­значать A .Попробуем определить это число.

Пусть имеем n элементов. Первый элемент можно выбрать п способами. Второй приходится выбирать из оставшихся п — 1 элементов, поэтому второй элемент можно выбрать п —1 спо­собом. Тогда по формуле (3.2) пары двух элементов можно об­разовать п(п — 1) способами. Третий элемент придется отбирать из числа оставшихся п — 2 элементов. Это можно сделать п — 2 способами. Тогда опять по формуле (3.2) тройки элементов можно образовать п (п — 1)(п — 2) способами. Аналогично чет­верки можно образовать п (п — 1) (п — 2) (п — 3) способами, а раз­мещения по m элементов

n (n — 1) (n — 2)...(n — (т — 1)) спосо­бами. Таким образом,

A = n(n — 1) (n —2)...(n — m + 1). (3.3)

Формулу (3.3) преобразуем, умножая и деля правую часть на произведение (n — т) (п — т — 1) (n — т — 2)...3 • 2 • 1. Получаем:

A =

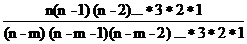
Математикиввели специальное название для произведенияn(n — 1) (n —2)…^.3^.2^.1.

Такое произведение называется факториалом числа п и обо­значается символом n!. Причем принято считать 0! = 1.

 

 

Формула (3.3) теперь приобретает удобную для запомина­ния форму:

A =

 

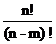
В случае, когда т = п, одно размещение от другого отличает­ся только порядком расположения элементов. Такие размеще­ния называются перестановками без повторений. Мы можем продолжать наши рассуждения по такой схеме:

 

 

когда обладают или признаком (а), или (б)

 

 

когда т = п и обладают признаком (б) и только (б)

 

Отсюда определение:

Перестановками без повторений из п элементов называются размещения без повторений из п элементов по п, т. е. размеще­ния, отличающиеся одно от другого только порядком распо­ложения элементов.

Характерный пример перестановок без повторений — вся со­вокупность всех десятизначных номеров, в каждом из которых нет повторения цифр.

Обозначим число перестановок объема п символом Р_n.

Тогда по определению и формуле (3.3)

Р_n =А^п = п(п - 1)(п - 2)...3^.2^.1, т. е.

Р_n =n! (3.5)

 

Среди размещений без повторений из п элементов по m (m<n) можно выделить такие, которые отличаются одно от другого (а) и только (а) признаком. Такие размещения на­зываются сочетаниями без повторений. Свои рассуждения мо­жем продолжать по такой схеме:

 

Когда обладают или признаком (а), или признаком (б)

 

 

когда m<n и обладают признаком (а) и только (а)

 

 

Определение:

Сочетаниями без повторений из п элементов по m называют­ся такие размещения без повторений из п элементов по т, ко­торые одно от другого отличаются хотя бы одним элемен­том.

Число таких сочетаний обозначается символом C . Разу­меется, при m = n,C = 1.

Характерный пример сочетаний без повторений — всевоз­можные варианты состава делегации в количестве, например, трех человек от коллектива, в котором 10 человек.

В каждом из C сочетаний имеется m различных элементов, поэтому на базе каждого сочетания можно получить Р_т пере­становок. Совокупность всех выборок, полученных путем пост­роения всех перестановок на базе каждого из C сочетаний, представляет собой число размещений A , т. е.

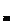C ^. P = A .

откуда

C = 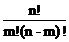^(3.6)

Всё нами рассмотренное в параграфе 2 можно привести к та­кой обобщающей схеме:

 

 

если одна от другой отличаются либо соста­вом элементов, либо порядком их располо­жения

 

 

если одно от другого отличаются, если одно от другого отлича­ются

только порядком расположения хотя бы одним элементом

элементов

 

Примеры

 

1. На тренировках занимаются 12 баскетболистов.

Сколько может быть образовано тренером разных стартовых пятерок?

Так как при составлении стартовой пятерки тренера интересует только состав пятерки, то достаточно определить число сочетаний из 12 элементов по 5:

 

C 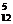= =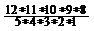792.

 

2. Сколькими способами можно расположить на шахматной доске 8 ладей так, чтобы они не могли взять друг дру­га?

Ясно, что в этом случае на каждой горизонтали и каждой вертикали шахматной доски может быть расположено только по одной ладье. Число возможных позиций — число перестано­вок из 8 элементов:

Р₈ = 8!=8^.7^.6^.5^.4^.3^.2^.1=40320.

3. Для полета на Марс необходимо укомплектовать следую­щий экипаж космического корабля: командир корабля, первый его помощник, второй помощник, два бортинженера и один врач. Командующая тройка может быть отобрана из числа 25 готовящихся к полету летчиков, два бортинженера — из числа 20 специалистов, в совершенстве знающих устройство косми­ческого корабля, и врач — из числа 8 медиков. Сколькими способами можно укомплектовать экипаж исследователей кос­моса?

При выборе командира и его помощников важно опреде­лить, какой из военных летчиков лучше других справляется с теми или иными функциями в управлении кораблем. Зна­чит, здесь важен не только персональный состав командующей тройки, но и соответствующая расстановка подобранных людей. Поэтому ясно, что командующая тройка может быть укомплектована, а 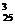способами.

Обязанности у обоих бортинженеров примерно одинаковые. Они могут выполнять их по очереди. Следовательно, пара борт­инженеров может быть укомплектована C 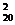способами. Анало­гичное положение и с врачом — его можно подобрать С 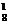спо­собами.

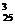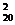В силу формулы (3.2) весь экипаж может быть укомплек­тован а C С 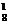= 20 976 000 способами.

 

Упражнения

 

28. В классе 30 учеников. Необходимо избрать старосту, комсорга и культорга класса. Сколькими способами можно об­разовать эту руководящую тройку, если одно лицо может зани­мать только один пост?

29. Сколько разных пятизначных чисел можно составить из цифр 1, 2, 3, 4 и 5 при условии, что ни одна цифра не повторяется?

30. Игрок сначала бросает белую игральную кость, потом черную. Сколько может быть случаев, когда число очков, поя­вившихся на белой кости, больше числа очков, появившихся на черной?

31. Сколько разных стартовых шестерок можно образовать из числа 10 волейболистов?

32. В кружке юных математиков 25 членов. Необходимо избрать председателя кружка, его заместителя, редактора стенга­зеты и секретаря. Сколькими способами можно образовать эту руководящую четверку, если одно лицо может занимать только один пост?

33. Школьная комсомольская организация, в которой на­считывается 150 членов, выбирает 6 делегатов на районную конференцию. Сколькими способами может быть избрана эта шестерка?

34. Сколько разных трехзначных чисел можно составить из цифр 1, 2, 3, 4 и 5 при условии, что ни одна цифра не повто­ряется?

35. В одной арабской сказке речь идет о такой задаче. Вокруг костра сидят 12 разбойников. Каждый из них смер­тельно ненавидит двух ближайших соседей. С целью спрятать награбленное необходимо выделить 5 разбойников. Сколькими способами атаман может назначить пятерых так, чтобы между ними не было распрей?

36. В колоде 32 карты. Раздаются 3 карты. Сколько может быть случаев появления одного туза среди розданных карт?

37. В пионерском отряде 4 звена по 8 пионеров. Выбираются 4 делегата на дружинный сбор. Что можно сказать о числе случаев избрания в делегаты хотя бы одного представителя первого отряда?

38. Сколько можно составить трехзначных чисел из цифр 1, 2, 3, 4 и 5, если цифры могут повторяться?

39. Сколько четырехзначных чисел можно составить из цифр 1 и 2?

40. На книжной полке плотно уставлено п книг. Сколь­кими способами можно взять с полки k книг при условии, что ни разу не будут вынуты рядом стоящие книги?

41. Докажите, что C = C .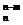

42. Докажите равенство Паскаля:

C 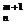+ C = C .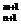

 

Программа на языке Бейсик для вычисления А :

8 RЕМ ПРОГРАММА ВЫЧИСЛЕНИЯ

9 RЕМ ЧИСЛА РАЗМЕЩЕНИЙ

10 INPUT "ВВЕДИТЕ М. N", М, N

20 IFN>=M THEN 50

30 PRINT "M>N"

40 GO TO 130

50 F = N

60 GOSUB 200

70 N1=F1

80 F = N — M

90 GOSUB 200

100 M1=F1

110 A=N1/M1

120 PRINT "ЧИСЛО РАЗМЕЩЕНИИ А = "; А

130 STOP

198 RЕМ ПОДПРОГРАММА ВЫЧИСЛЕНИЯ

199 REM ФАКТОРИАЛА

200 Fl = l

210 F2 = 0

220 IF F = F2 THEN 260

230 F2 = F2 + 1

240 F1 = F1 * F2

250 GO TO 220

260 RETURN

270 END