Вероятностью случайного события A называется отношение числа m элементарных исходов испытания, благоприятствующих событию А, к числу n всех единственно возможных и равновозможных элементарных исходов, образующих полную группу.
.
Исходы, при которых событие А происходит, называется благоприятствующими событию А. Если в результате испытания наступает единственное событие, то говорят, что осуществляется единственно возможный элементарный исход испытания.
Для вычисления числа благоприятствующих рассматриваемому событию исходов или общего числа элементарных исходов широко используются формулы комбинаторики.
Если составляются такие комбинации из n элементов по k, которые отличаются друг от друга только составом элементов, то они называются сочетаниями. Общее число сочетаний из n элементов по k определяется по формуле
,
где п! = 1∙2∙…∙ п, 0! = 1.
Если комбинации отличаются не только составом элементов, но и их порядком, то они называются размещениями. Их число находят по формуле
.
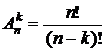Если комбинации берутся из всех n элементов и отличаются только порядком следования элементов, то они называются перестановками. Их число равно 
ПРИМЕР. В научно-техническом отделе предприятия работают 15 человек, 10 из них мужчины. Для участия в конференции необходимо отобрать 5 сотрудников. Какова вероятность того, что среди отобранных сотрудников трое мужчин.
РЕШЕНИЕ. Пусть событие A означает, что из пяти отобранных для участия в конференции сотрудников трое мужчин. Тогда
.
Общее число n способов выбора сотрудников равно числу сочетаний из 15 по 5, т.е. 
. Определим число m благоприятствующих событию А исходов – «среди отобранных пяти сотрудников будет трое мужчин». Выбрать трех мужчин из десяти можно 
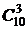способами. Каждому такому выбору соответствует 
способов выбора двух женщин из пяти. Следовательно, 
.Тогда
= 
= 
= 
= 
= 
= 
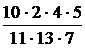0,3996.
Ответ: 
.
ЗАДАНИЕ 4
Рассмотрим n случайных событий А 1, А 2, …, Ап.
Суммой (объединением) событий А 1, А 2, …, Ап называется событие В = А 1 + А 2 + … + Ап = 
, состоящее в появлении хотя бы одного из этих событий.
Произведением (пересечением) событий А 1, А 2, …, Ап называется событие С = А 1∙ А 2∙…∙ Ап = 
, обозначающее появление всех перечисленных событий.
События А 1, А 2, …, Ап называются попарно несовместными, если в одном и том же опыте никакие два из них не могут произойти вместе.
Теорема. Вероятность суммы попарно несовместных событий равна сумме вероятностей этих событий:
Р (А 1 + А 2 + … + Ап) =Р (А 1) + Р (А 2) + … + Р (Ап).
Событием, противоположным событию А, называется событие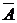 
, состоящее в не наступлении события А. Очевидно, события А и 
несовместны, поэтому Р (А) = 1 – Р ().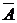
Случайные события А 1, А 2, …, Ап называются независимыми в совокупности, если вероятность появления любого из них не зависит от того, произошли ли какие-либо другие из этих рассматриваемых событий или нет.
Теорема. Вероятность произведения случайных событий А 1, А 2, …, Ап, независимых в совокупности, равна произведению их вероятностей:
Р (А 1∙ А 2∙…∙ Ап) =Р (А 1)∙ Р (А 2)∙…∙ Р (Ап).
ПРИМЕР. Вероятности своевременного выполнения студентом контрольной работы по каждой из трех дисциплин, соответственно равны p 1=0,8, p 2=0,9, p 3=0,7. Найти вероятность своевременного выполнения контрольной работы студентом:
1) только по одной дисциплине;
2) не более чем по двум дисциплинам;
3) хотя бы по одной дисциплине.
РЕШЕНИЕ. Пусть Аi (i = 1, 2,3) – события, означающие, что студент своевременно выполнит контрольную работу по каждой из трёх дисциплин. Тогда Р (А 1) = 0,8; Р (А 2) = 0,9; Р (А 3) = 0,7. Обозначим 
, (i = 1, 2,3) – события, означающие, что студент не своевременно выполнит контрольную работу по каждой из трёх дисциплин. Тогда
Р (
) = 1 – 0,8 = 0,2; Р (
) = 1 – 0,9 = 0,1; Р (
) = 1 – 0,7 = 0,3.
1) Пусть А событие, состоящее в том, что студент своевременно выполнит контрольную работу только по одной дисциплине. Тогда, имеем:
.
Так как 
– несовместные, а , (i = 1, 2,3) независимые в совокупности события, то применяя теорему о вероятности суммы несовместных событий и теорему о вероятности произведения независимых событий, получим:
.
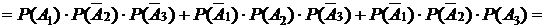
2) Событие 
, состоящее в том, что студент своевременно выполнит контрольную работу не более чем по двум дисциплинам. Событие есть сумма несовместных событий, означающих, что своевременно будут выполнены контрольные работы по двум, или только по одной, или ни по одной дисциплине. В символьной записи имеем:
Применяя теорему о вероятности суммы несовместных событий и теорему о вероятности произведения независимых событий, получим:
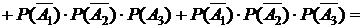
3) Событие С, состоящее в том, что студент своевременно выполнит контрольную работу хотя бы по одной дисциплине, есть сумма событий 
. Противоположным для этого события является событие 
, состоящее в том, что студент не своевременно выполнит контрольные работы по всем трем дисциплинам. Оно может быть представлено в виде произведения независимых событий: 
. Учитывая теорему о вероятности произведения независимых событий, имеем:
= 
.
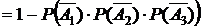
Ответ: 1) 
; 2) 
3) 
.
ЗАДАНИЕ 5
Рассмотрим конечную последовательность п независимых испытаний, в результате каждого из которых может произойти событие А или ему противоположное 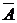с вероятностями р и q = 1 – p соответственно, причем вероятность р не меняется от опыта к опыту. По условию результат любого испытания не зависит от его порядкового номера и от того, какие исходы были в предыдущих испытаниях. Такую последовательность испытаний принято называть схемой испытаний Бернулли. Приняты следующие обозначения:
Pn (m) – вероятность того, что событие A произойдёт ровно m раз в серии из n испытаний;
Pn (m ≥ k) = Pn (k) + Pn (k + 1) + … + Pn (n) – вероятность того, что событие A произойдёт не менее чем k раз в серии из n испытаний;
Pn (m ≤ k) = Pn (0) + Pn (1) + … + Pn (k) – вероятность того, что событие A произойдёт не более чем k раз в серии из n испытаний;
Pn (m ≥ 1) = 1 – Pn (0) – вероятность того, что событие A произойдёт хотя бы один раз в серии из n испытаний.
При нахождении нужной вероятности необходимо учитывать заданные значения n и p. При выборе формулы для Pn (m) надо руководствоваться следующими правилами:
1) если задано число испытаний n и оно не больше 10, то следует пользоваться формулой Бернулли
Pn (m) = 
∙ pm ∙ qn – m;
2) если вероятность р наступления события A мала, а n велико и λ = np < 10, то следует воспользоваться формулой Пуассона:
Pn (m) ≈ 
∙ e – λ, Pn (m ≤ k) ≈ e – λ 
;
3) если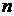 
велико и 
, то следует воспользоваться локальной теоремой Муавра-Лапласа. По этой теореме
Pn (m) ≈ 
∙φ(x), где φ(x) = 
∙ 
; x = 
.
Функция φ(x) – чётная и для x ≥ 0 имеется таблица значений этой функции, для x > 4 φ(x) ≈ 0 (см. [4], приложения: таблица 3,с. 305 – 306).
Если требуется найти вероятность того, что в серии из n независимых испытаний число наступлений события A будет не менее k 1 и не более k 2 раз – Pn (k 1, k 2) = Pn (k 1 ≤ m ≤ k 2), то следует воспользоваться интегральной теоремой Муавра-Лапласа. По этой теореме
Pn (k 1, k 2) ≈ Ф (х 2) – Ф (х 1),
где
Ф (х) =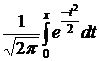 
, x 1 = 
, x 2 = 
.
Ф (х) называется функцией Лапласа. Она нечётная Ф (– х) = – Ф (х). Таблица значений этой функции составлена для x ≥ 0. Если x ≥ 5, то Ф (х) ≈ 0,5 (см. [4], приложения: таблица 4, с. 306 – 307).
ПРИМЕР 1. Всхожесть семян лимона составляет 60%. Определить вероятность того, что из шести посеянных семян взойдут:
1) хотя бы один лимон;
2) ровно три лимона;
3) не более трех лимонов.
РЕШЕНИЕ. Так как п = 6 < 10, то воспользуемся формулой Бернулли. По условию всхожесть семян составляет 60%. Тогда вероятность того, что случайным образом взятое семечко взойдет, равна p = 0,6, q = 1 – 0,6 = 0,4.
1) Вероятность того, что хотя бы одно из шести случайно взятых семян лимона взойдет, вычислим по формуле
P 6(m ≥ 1) = 1 – P 6(0) = 1 – q 6 = 1 – 0,46 = 1 – 0,004096 = 0,995904 ≈ 0,996.
2) Вероятность того, что среди шести случайно взятых семян взойдут ровно три лимона, равна
P 6(3) = 
∙ p 3∙ q 3 = 
∙0,63∙0,43 = 20∙0,013824 = 0,27648 ≈ 0,28.
3) Вероятность того, что среди шести случайно взятых семян взойдут не более трех лимонов, равна
P 6(m ≤ 3) = P 6(0) + P 6(1) + P 6(2) + P 6(3) = 0,46 + 
∙ p 1∙ q 5 + 
∙ p 2∙ q 4 + ∙ p 3∙ q 3 =
= 0,004096 + 6∙0,6∙0,01024 + 15∙0,36∙0,0256 + 0,27648 =
= 0,004096 + 0,036864 + 0,13824 + 0,27648 = 0,45568 ≈ 0,46.
Ответ: 1) 0,0996; 2) 0,28; 3) 0,46.
ПРИМЕР 2. Завод отправил на базу n = 500 стандартных изделий. Вероятность того, что изделие при транспортировке будет повреждено, равна р = 0,001. Найти вероятность того, что при транспортировке будет повреждено:
1) хотя бы одно изделие;
2) ровно три изделия;
3) не более трех изделий.
РЕШЕНИЕ. Количество стандартных изделий n = 500 велико, а вероятность того, что при транспортировке изделие будет повреждено, р = 0,001 мала и λ = np = 0,5 < 10. Следовательно, необходимо воспользоваться формулой Пуассона:
Pn (m) ≈ ∙ e – λ, где λ = np = 0,5.
1) Найдём вероятность того, что при транспортировке будет повреждено хотя бы одно изделие.
P 500(m ≥ 1) = 1 – P 500(0) ≈ 1 – 
= 1 – 
= 1 – 0,60653 ≈ 0,40
(по определению 0! = 1).
2) Найдём вероятность того, что при транспортировке будет повреждено ровно три изделия:
P 500(3) ≈ 
= 0,125∙ 
∙ ≈ 0,01.
3) Найдём вероятность того, что при транспортировке будет повреждено не более трех изделий:
P 500(m ≤ 3) = P 500(0) + P 500(1) + P 500(2) + P 500(3) ≈
= 0,61 + 
+ 
+ ≈ 0,61 + 0,3 + 0,08 + 0,01 = 1.
Ответ: 1) 0,40; 2) 0,01; 3) 1.
ПРИМЕР 3. Строительная фирма, занимающаяся установкой летних коттеджей, раскладывает рекламные листки по почтовым ящикам. Прежний опыт работы компании показывает, что вероятность того, что фирма получит заказ, равна 0,2. Найти вероятность того, что при размещении 400 листков число заказов будет:
1) хотя бы один;
2) ровно 90 заказов;
3) не более 90 заказов.
РЕШЕНИЕ. Так как п = 400 велико, р = 0,2 и λ = np = 80 > 10, то для нахождения требуемых вероятностей необходимо воспользоваться локальной и интегральной теоремами Муавра-Лапласа.
.
1) Найдём вероятность того, что при размещении 400 листков, фирма получит хотя бы один заказ:
P 400(m ≥ 1) = 1 – P 400(0) ≈ 1 – ∙φ 
≈
≈ 1 – 
∙φ 
≈ 1 – ∙φ(– 10) ≈ 1 – 0 = 1.
2) Найдём вероятность того, что при размещении 400 листков, фирма получит ровно 90 заказов:
P 400(90) ≈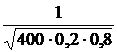 
∙φ 
≈ ∙φ 
≈
≈ ∙φ(1,25) ≈ ∙0,1826 ≈ 0,0228.
3) Найдём вероятность того, что при размещении 400 листков, фирма получит не более 90 заказов. Здесь k 1 = 0, k 2 = 90. Тогда
P 400(0; 90) ≈ Ф (х 2) – Ф (х 1),
где x 1 = = 
= – 10, x 2 = 
= 
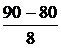= 1,25.
По таблице значений функции Лапласа находим: Ф (х 2) = Ф (1,25) ≈ 0,3944, Ф (х 1) = Ф (– 10) = – Ф (10) ≈ – 0,5. Поэтому
P 400(0; 90) ≈ 0,3944 – (– 0,5) = 0,8944.
Ответ: 1) 1; 2) 0,0228; 3) 0,8944.
ЗАДАНИЕ 6
Величина, которая в ходе опыта может принимать только одно из своих возможных значений, заранее неизвестное, называется случайной величиной. В зависимости от возможных значений все случайные величины разбиваются на два класса: дискретные и непрерывные.
Дискретной называется случайная величина, возможные значения которой отдельные изолированные числа. Количество значений образует или конечное множество, или бесконечное, но счётное (бесконечное множество, элементы которого можно пронумеровать и выписать в виде последовательности).
Законом распределения дискретной случайной величины называется всякое правило, по которому каждому возможному значению xi ставится в соответствие вероятность pi, с которой случайная величина может принять это значение. Поскольку в результате опыта случайная величина может принять одно и только одно из возможных значений, то событие, заключающееся в том, что случайная величина X примет значения x 1, x 2, …, xn, попарно несовместны и в сумме образуют достоверное событие. Отсюда следует, что вероятность суммы этих событий равна 1 и, следовательно, 
= 
= 1.
Для описания случайной величины часто используют её числовые характеристики. К ним относятся математическое ожидание М (Х) (характеризует среднее значение случайной величины) и дисперсия D (X) (характеризует разброс значений случайной величины относительно её математического ожидания). Для дискретной случайной величины они вычисляются по формулам:
М (Х) = х 1 р 1 + х 2 р 2 + … + хпрп = 
;
D (X) = М (Х – М (Х))2 = 
= 
– (М (Х))2.
ПРИМЕР. Дискретная случайная величина Х задана рядом распределения
Таблица 10 – Ряд распределения
| Х | – 1 | х 3 | ||
| р | 0,2 | 0,3 | 0,1 | р 4 |
Зная математическое ожидание М (Х) = 0,7 случайной величины, найти:
а) р 4;
б) х 3;
в) дисперсию D (x).
РЕШЕНИЕ. а) Так как для закона распределения дискретной случайной величины должно выполняться условие = 1, то в данном случае имеем:
= 0,2 + 0,3 + 0,1 + р 4 = 1,
то есть
0,6 + р 4 = 1
и, следовательно, р 4 = 0,4.
б) Математическое ожидание M (X) дискретной случайной величины равно
M (X) = 
.
Тогда
M (X) = – 1∙0,2 + 0∙0,3 + х 3∙0,1 + 2∙0,4 = 0,7,
то есть
х 3∙0,1 + 0,6 = 0,7,
х 3∙0,1 = 0,1
и, следовательно, х 3 = 1.
в) Найдём дисперсию D (X) дискретной случайной величины Х:
D (X) = 
– (M (X))2 = (– 1)2∙0,2 + (0)2∙0,3 + (1)2∙0,1 + (2)2∙0,4 – (0,7)2 = 1,41.
Ответ: а) р 4 = 0,4; б) х 3 = 1; в) D (X) = 1,41.
ЗАДАНИЕ 7
Если случайная величина Х имеет нормальное распределение с параметрами а и σ, то вероятность того, что Х примет значение, принадлежащее интервалу (α; β), вычисляется по формуле:
Р (α < X < β) = Ф 
– Ф 
,
где Ф (х) = 
– функция Лапласа.
Вероятность того, что абсолютная величина отклонения значений случайной величины Х от её математического ожидания а меньше заданного положительного числа δ, выражается равенством:
Р (| X – а | < δ) = 2∙ Ф 
.
Если, в частности, δ = 3σ, то
Р (| X – а | < 3σ) = 2∙ Ф (3) = 0,9973 ≈ 1,
то есть нормально распределенная случайная величина Х отклонится от своего математического ожидания а, как правило, менее чем на 3σ (правило трех сигм).
ПРИМЕР. Текущая цена ценной бумаги представляет собой нормально распределенную случайную величину Х со средним равным 100 усл. ед. и дисперсией равной 9. Найти:
1) вероятность того, что цена актива будет находиться в пределах от 90 до 110 усл. ед.;
2) вероятность того, что абсолютная величина отклонения | Х – а | окажется меньше 2;
3) сформулировать «правило трех сигм» для случайной величины Х.
РЕШЕНИЕ. 1) Так как α = 100, σ =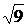 
= 3, то
Р (90 < X < 110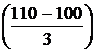) = Ф 
– Ф 
= Ф (3,33) – Ф (– 3,33) =
= 2∙ Ф (3,33) = 0,9994.
2) По формуле
Р (| X – а | < δ) = 2∙ Ф
имеем
Р (| Х – α| < 2) = 2∙ Φ 
= 2∙ Φ (0,67) = 2·0,2486 = 0,4972.
3) Практически достоверно, что цена актива будет заключена в границах от а – 3σ = 100 – 3∙3 = 91 до а + 3σ = 100 + 3∙3 = 109 (усл. ед.), то есть 91 ≤ Х ≤ 109 (усл.ед.).
Ответ: 1) р = 0,9994; 2) р = 0,4972; 3) 91 ≤ Х ≤ 109.
ЗАДАНИЕ 8. При обследовании 60 семей рабочих и служащих установлен следующей количественный состав семьи:
Таблица 11 – Количество членов семьи
Требуется:
1) составить интервальный статистический ряд распределения значений статистических данных;
2) построить гистограмму и полигон относительных частот;
3) найти эмпирическую функцию распределения и построить её график;
4) вычислить числовые характеристики выборки (выборочную среднюю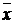 
, выборочное среднее квадратичное отклонение σ В (Х)).
РЕШЕНИЕ. 1) Изучение непрерывных случайных величин начинают с разбивки интервала изменения случайной величины на т частичных интервалов равной длины и подсчета частоты попадания значений случайной величины в каждый интервал. Обычно таких интервалов берётся т ≈ 1 + 3,2∙lg n. (Эта формула рекомендуется при проверке гипотезы о виде закона распределения изучаемой случайной величины. Вообще говоря, строгих правил для выбора числа интервалов группирования не существует. Практический же опыт первичного анализа статистических данных показывает, что удовлетворительным является число интервалов от 5 до 15).
В нашем случае x min = 1, x max = 9, т ≈ 1 + 3,2∙lg n = 1 + 3,2∙lg60 = 6,69,
= 
≈ 1,2.
Длину интервала удобно выбрать так, чтобы последняя цифра была четной. Тогда и середина интервала 
будет иметь последнюю цифру того же десятичного разряда, что и концы интервала. Начало первого интервала принимаем равным 
Тогда первый интервал будет [1 – 2,2 ], второй – 
и т.д.
Шкалу интервалов и группировку статистических данных представим в виде таблицы 12.
Таблица 12 – Интервальный статистический ряд
| интервалы | [1; 2,2] | (2,2; 3,4] | (3,4;4,6] | (4,6;5,8] | (5,8;7] | (7;8,2] | (8,2;9,4] |
| Частота mi | |||||||
Относительная частота 
| 0,1 | 0,1 | 0,15 | 0,2 | 0,25 | 0,1 | 0,1 |
| Накоплен-ная относ. частота | 0,1 | 0,2 | 0,35 | 0,55 | 0,8 | 0,9 |
Таким образом, мы составили интервальный статистический ряд распределения значений статистических данных.
2) Строим гистограмму и полигон относительных частот. На оси Ox откладываем частичные интервалы длины h = 1,2, а на каждом интервале, как на основании, строим прямоугольник с высотой, пропорциональной относительной частоте интервала (с высотой, равной 
).
Соединим середины верхних оснований отрезками прямых линий, получим полигон относительных частот (рисунок 4).
Рисунок 4 – Гистограмма и полигон относительных частот
3) Эмпирическую функцию распределения получим с помощью накопленных относительных частот.
Построим график функции F* (x) (рисунок 5).
Рисунок 5 – График функции 
4) Найдем числовые характеристики выборки.
Выборочную среднюю найдем по формуле 
= 
, здесь yi –середина i -го интервала, mi – частота i -го интервала, m – количество интервалов.
Выборочную дисперсию найдем по формуле
или
.
Так как объём выборки п = 60 велик, то выборочная дисперсия и исправленная выборочная дисперсия практически совпадают. Для упрощения вычислений используем таблицу 12.
Таблица 13 – Данные для расчета числовых характеристик
| Интервалы | Середина интервала yi | Частота mi | 
| 
| (yi –  )2∙ mi
|
| [1 – 2,2] | 1,6 | 9,6 | –3,7 | 82,14 | |
| (2,2 – 3,4] | 2,8 | 16,8 | –2,9 | 50,46 | |
| (3,4 – 4,6] | 4,0 | 36,0 | –1,3 | 15,21 | |
| (4,6 – 5,8] | 5,2 | 62,4 | –0,1 | 0,12 | |
| (5,8 – 7] | 6,4 | 96,0 | 1,1 | 18,15 | |
| (7 – 8,2] | 7,6 | 45,6 | 2,3 | 31,74 | |
| (8,2 – 9,4] | 8,8 | 52,8 | 3,5 | 73,50 | |
| Сумма | 319,2 | 271,32 |
Таким образом, имеем: 
5,3; 
4,6.
Выборочное среднее квадратичное отклонение σ В = s = 
= 2,1.
ВОПРОСЫДЛЯ ПОРДГОТОВКИ К ЭКЗАМЕНУ
Кратные интегралы
1 Задачи, приводящие к понятию двойных интегралов.
2 Двойной интеграл. Теорема существования.
3 Свойства двойного интеграла.
4 Вычисление двойного интеграла в декартовых координатах.
5 Криволинейные координаты, якобиан преобразования. Двойной интеграл в полярных координатах.
6 Приложения двойных интегралов.
7 Определение тройного интеграла. Физический и геометрический смысл тройного интеграла.
8 Вычисление тройного интеграла в декартовых координатах.
9 Тройной интеграл в цилиндрических и сферических координатах.
10 Приложения тройных интегралов.
Криволинейные интегралы
11 Криволинейные интегралы первого рода: определение, вычисление, свойства, приложения.
12 Криволинейные интегралы второго рода: определение, вычисление, свойства, приложения.
13 Формула Грина.
Теория вероятностей.
14 Предмет и задачи теории вероятностей.
15 Элементы комбинаторики.
16 Пространство элементарных событий.
17 Алгебра событий.
18 Классическое, статистическое и геометрическое определения вероятности.
19 Основные теоремы теории вероятностей: вероятность суммы несовместных и совместных событий, вероятность произведения зависимых и независимых событий.
20 Формула полной вероятности. Вероятность гипотез.
21 Схема испытаний Бернулли. Формула Бернулли.
22 Теорема Пуассона.
23 Локальная и интегральная теоремы Лапласа.
24 Наивероятнейшее число появлений события при повторных испытаниях по схеме Бернулли.
25 Вероятность отклонения относительной частоты от постоянной вероятности в независимых испытаниях.
26 Случайные величины (СВ) дискретные и непрерывные.
27 Дискретные случайные величины (ДСВ). Закон распределения.
28 Функция распределения и ее свойства.
29 Числовые характеристики дискретных случайных величин и их свойства.
30 Законы распределения дискретных случайных величин и их числовые характеристики: биномиальное, геометрическое, распределение Пуассона.
31 Непрерывные случайные величины (НСВ). Дифференциальная функция распределения непрерывной СВ и ее свойства.
32 Равномерный и показательный законы распределения НСВ и их числовые характеристики.
33 Простейший поток событий.
34 Нормальный закон распределения НСВ и его числовые характеристики.
35 Свойства и график плотности нормально распределенной СВ, вероятность попадания в интервал.
36 Закон больших чисел. Неравенство Чебышева, теоремы Чебышева, Бернулли, Ляпунова (без доказательства).
37 Двумерные СВ. Функция распределения системы двух СВ и ее свойства. Плотность распределения двумерной СВ.
38 Законы распределения системы СВ и их составляющих.
39 Числовые характеристики системы СВ, корреляционный момент и коэффициент корреляции.