21.04.2020
Углы со взаимно перпендикулярными и взаимно параллельными сторонами.
Углы с соответственно параллельными сторонами.
Возьмём на плоскости две точки С и О и из этих точек проведём две пары лучей
СА || ОМ и СВ || ОN так, чтобы углы АСВ и МОN были или оба острые (рис. 1), или оба тупые (рис. 2).
 Рис. 1
Рис. 1
|  Рис. 2
Рис. 2
|
Углы АСВ и МОN — углы с соответственно параллельными cторонами. Докажем, что эти углы равны между собой.
Пусть СВ пересекает ОМ в точке D.  , как соответственные углы при параллельных АС и МО и секущей СВ.
, как соответственные углы при параллельных АС и МО и секущей СВ.
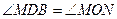 , как соответственные углы при параллельных СВ и ОN и секущей МО, но тогда и
, как соответственные углы при параллельных СВ и ОN и секущей МО, но тогда и  .
.
Следовательно, углы с соответственно параллельными сторонами равны, если они оба острые или оба тупые.
 Рис.3
Рис.3
| Построим два острых угла АСВ и МОN с соответственно параллельными сторонами (рис. 3): СА || МО и СВ || ОN, и продолжим за вершину О стороны угла МОN.
При вершине О образовались два тупых угла ЕОМ и FОN (так как смежный с ними угол МОN по построению острый).
Каждый из них в сумме с углом МОN составляет 2 d, а так как  , то , то  и и  . .
|
Следовательно, углы с соответственно параллельными сторонами в сумме составляют 2 d, если один из них острый, а другой тупой.
Углы с соответственно перпендикулярными сторонами.
 Рис. 4
Рис. 4
| Построим произвольный острый угол АВС. Проведём через вершину угла лучи, перпендикулярные к его сторонам, так, чтобы они образовали острый угол. BO_|_ ВС и ВК _|_ АВ (рис. 4). Мы получим новый угол OBK. Стороны углов AВС и ОВК взаимно перпендикулярны. / АВС = d — / СВК; / ОВК = d — / СВК. Отсюда следует, что / АBС = / ОВК. |
| Построим произвольный тупой угол АОВ и через его вершину проведём лучи, перпендикулярные к его сторонам, так, чтобы они образовали тупой угол. ОК_|_ОА и ОС_|_ОВ (рис. 5), угол КОС — тупой. Стороны углов АОВ и КОС взаимно перпендикулярны, поэтому / АОВ = d + / КОВ; / КОС = d + / КОВ. Отсюда следует, что / АОВ = / КОС. |  Рис. 5
Рис. 5
|
Углы с соответственно перпендикулярными сторонами равны между собой, если они оба острые или оба тупые.
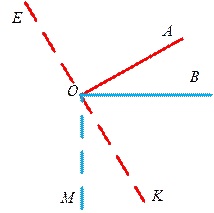 Рис. 6 Рис. 6
| Построим произвольный острый угол АОВ и проведём через его вершину перпендикуляры к его сторонам так, чтобы они образовали острый угол (рис. 6). Получим: / КОМ = / АОВ. Продолжим сторону ОК за вершину О. Стороны угла ЕОМ перпендикулярны сторонам угла АОВ. При этом / ЕОМ — тупой, так как смежный с ним / МОК — острый. / КОМ + / ЕОМ = 2 d (как углы смежные). Но / КОМ по ранее доказанному равен / АОВ. Следовательно, и / АОВ + / ЕОМ = 2 d. |
Углы с соответственно перпендикулярными сторонами в сумме составляют 2 d, если один из них острый, а другой тупой.
Мы рассматривали углы, составленные взаимно перпендикулярными сторонами, когда они имели общую вершину. Выведенные нами свойства будут справедливы и в том случае, когда углы не будут иметь общей вершины.
 Рис. к задаче 1
Рис. к задаче 1
| Задача 1.Две взаимно перпендикулярные прямыепересекают стороны AB, BC, CD, AD квадрата ABCD в точках E, F, K, L соответственно. Доказать, что EK = FL (см. рис. к задаче 1).
Решение. Используя первый из указанных выше путей равенства двух отрезков, проведем отрезки  и и 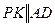 . Тогда интересующие нас отрезки EK и FL станут сторонами двух прямоугольных треугольников EPK и FML. Имеем: PK = FM. Так как: PK = AD, AD = AB, AB = FM, значит, PK = FM. Углы . Тогда интересующие нас отрезки EK и FL станут сторонами двух прямоугольных треугольников EPK и FML. Имеем: PK = FM. Так как: PK = AD, AD = AB, AB = FM, значит, PK = FM. Углы 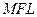 и и  равны между собойкак углы со взаимно перпендикулярными сторонами. Значит, (по катету и острому углу) прямоугольные треугольники равны между собойкак углы со взаимно перпендикулярными сторонами. Значит, (по катету и острому углу) прямоугольные треугольники  и и  равны между собой. Из равенства прямоугольных треугольников следует равенство их гипотенуз, т.е. отрезков EK и FL. равны между собой. Из равенства прямоугольных треугольников следует равенство их гипотенуз, т.е. отрезков EK и FL.
|