Разработана математическая модель, исследование которой позволит определить параметры движения подводной лодки под водой при всплытии.
Объектом моделирования является тело, движущееся под водой.
Наполнение лодки воздухом в момент начала всплытия происходит мгновенно, масса лодки не изменяется. Сопротивлением воды пренебрегаем.
Лодку можно считать материальной точкой массой m, положение которой совпадает с центром масс лодки.
Движение лодки может быть описано в соответствии с законами механики Ньютона, на лодку действует выталкивающая сила воды в соответствии с законом Архимеда.
Движение лодки происходит в одной плоскости, перпендикулярной поверхности Земли.
Ускорение свободного падения тела и средняя плотность воды с глубиной погружения лодки не изменяются.
Исходные данные: объем лодки, начальная глубина, скорость движения (постоянная горизонтальная), средняя плотность воды, средняя плотность наполненной воздухом лодки при всплытии.
V - объем лодки [м3];
H - начальная глубина [м];
v - скорость движения (постоянная горизонтальная) [м/с];
ρ 1 - средняя плотность наполненной воздухом лодки при всплытии [кг/м3];
∆ L – точность определения дальности всплытия [м].
Принятые физические параметры:
g 0 - ускорение свободного падения [м/сек2];
ρ 0 - средняя плотность воды [кг/м3].
В качестве параметров движения лодки примем: координаты (х и у) и скорость (ее проекции v x и v y) центра масс лодки.
Тогда для определения положения лодки в любой момент времени достаточно найти закон движения ее центра масс, т.е. зависимость координат х, у и проекций вектора скорости v x и v y центра лодки от времени.
При всплытии на лодку начинает действовать выталкивающая сила, большая, чем вес лодки.
 По закону Архимеда выталкивающая сила равна
По закону Архимеда выталкивающая сила равна
F = gVρ 0.
Суммарная сила, действующая на лодку в вертикальном направлении, - разность между F и весом тела P = gV ρ 1.
Сообщаемое лодкой ускорение по второму закону Ньютона равно
ρ 1 V d 2 h / dt 2 = F – Р = gV (ρ 0 - ρ 1).
Координата l, характеризующая горизонтальное положение лодки, изменяется по закону движения тела с постоянной скоростью (вертикальная скорость лодки, а также величины l и h в момент t = 0 равны нулю): d l /d t = v.
Решая эти уравнения, находим, что

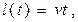 (1)
(1)
и что лодка всплывет на поверхность в момент t = t k, когда
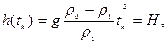
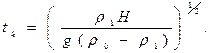
При этом в горизонтальном направлении лодка пройдет расстояние L = vt k.
Исключая из (1) время, найдем траекторию движения лодки в координатах (l, h)
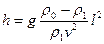 .
.
Траектория оказывается параболой с вершиной в точке l = 0, h = 0 (уравнение (1) фактически дает параметрическую запись параболы).
При движении тела в жидкости (или газе), тело увлекает за собой некоторую массу жидкости – присоединенную массу. Это обусловлено силами взаимодействия частиц - поверхностными силами – силами, приложимыми к элементу жидкости со стороны прилегающих к нему частиц остальной части жидкости. В первом приближении, для исследования степени учета ее влияния на результат, присоединенная масса может быть определена по формуле: m = 0,5 Vρ 0.
Задание
1. На основании приведенных математических соотношений разработать постановку задачи моделирования и математическую модель в соответствии с основными этапами моделирования (конспект лекций «Раздел 4 Этапы построения моделей»). Исходные данные – произвольные.
2.Определить тип траектории движения судна.
3.Выбрать адекватную математическую модель для различных диапазонов изменения исходных данных и определить дальность всплытия.
4.Построить траекторию всплытия судна для наиболее сложной математической модели и выбранных конкретных исходных данных из диапазона, в котором она обеспечивает решение этой задачи с заданной точностью.
Исходные данные и диапазоны их изменения – произвольные.
Оформить задание в виде презентации.
Пример анализа модели
Задача о баскетболисте.
Разработать математическую модель, исследование которой позволит определить параметры движения баскетбольного мяча, брошенного игроком в баскетбольную корзину.
Требования к модели: модель должна позволять вычислять положение мяча в любой момент времени, определять точность попадания мяча в корзину после броска при различных начальных параметрах.
Исходные данные: масса и радиус мяча, начальные координаты, скорость и угол бросания мяча, координаты центра и радиус корзины.
Движение мяча может быть описано в соответствии с законами механики Ньютона.
Примем гипотезы:
- объект моделирования – мяч радиуса R;
- мяч будем считать материальной точкой массой m, положение которой совпадает с центром масс мяча;
- движение происходит в поле сил тяжести с постоянным ускорением свободного падения g и описывается уравнениями классической механики Ньютона;
- движение мяча происходит в одной плоскости, перпендикулярной поверхности Земли и проходящей через точку броска и центр корзины;
- пренебрегаем сопротивлением воздуха и возмущениями, вызванными собственным вращением мяча вокруг центра масс.
В соответствии с гипотезами в качестве параметров движения мяча примем: координаты (х и у) и скорость (ее проекции v x и v y центра масс мяча.
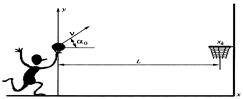 Тогда для определения положения мяча в любой момент времени достаточно найти закон движения центра масс мяча, т.е. зависимость координат х, у и проекций вектора скорости v x и v y центра мяча от времени.
Тогда для определения положения мяча в любой момент времени достаточно найти закон движения центра масс мяча, т.е. зависимость координат х, у и проекций вектора скорости v x и v y центра мяча от времени.
В качестве оценки точности броска D можно рассматривать величину расстояния по горизонтали (вдоль оси х) от центра корзины до центра мяча в момент, когда последний пересекает горизонтальную плоскость, проходящую через плоскость кольца корзины.
Определить закон движения материальной точки массой т под действием силы тяжести, если известны начальные координаты точки x 0 и у 0, ее начальная скорость v 0 и угол бросания a0.
Центр корзины имеет координаты хk и уk.
Вычислить точность броска D= x (tk) – хk, где tk определяется из условий: tk > 0, vy < 0, y (tk) = уk.
Математическую постановку задачи можно представить как в векторной, так и в координатной форме.
Координатная форма.
Найти зависимости x (t), y (t) и v x(t), v y(t) из решения системы дифференциальных уравнений:
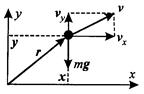 m
m  , vx =
, vx = 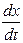 ,
,
m 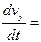 - mg, vy =
- mg, vy = 
при следующих начальных условиях:
x (0) = x 0, y (0) = y 0,
v x(0) = v 0 cos α0, vy (0) = v 0 sin α0.
Вычислить параметр D по формуле D = x (t k) – x k, где t k определить из условий t k > 0, v y(t k) < 0, y (t k) = y k.
Как можно видеть с математической точки зрения задача о баскетболисте свелась к задаче Коши для системы обыкновенных дифференциальных уравнений первого порядка с заданными начальными условиями (по заданным в начальный момент переменным определяются их значения для любого момента времени).
Полученная система уравнений является замкнутой, так как число независимых уравнений (четыре дифференциальных и два алгебраических) равно числу искомых параметров задачи (x, y, v x, v y, D, t k).
Анализ гипотез.
1-я гипотеза выделяет объект моделирования (мяч радиуса R).
В данном случае объект можно считать простым. Однако в качестве объекта моделирования можно рассматривать систему «игрок – мяч – кольцо». Требуемая для описания подобной системы модель будет уже намного сложнее, так как игрок в свою очередь представляет сложную биомеханическую систему и его моделирование является далеко не тривиальной задачей. В данной ситуации выбор в качестве объекта моделирования только мяча обоснован, поскольку именно его движение требуется исследовать, а влияние игрока можно учесть достаточно просто через начальные параметры броска. Для сложных систем выбор объекта моделирования – далеко не простая и неоднозначная задача.
2-я гипотеза (мяч можно считать материальной точкой массой m, положение которой совпадает с центром масс мяча) широко применяется для исследования движений тел в механике. В рассматриваемом случае она оправдана в силу симметрии формы мяча и малости его радиуса по сравнению с характерными расстояниями перемещения мяча. Предполагается, что последний является шаром с одинаковой толщиной стенки.
3-я гипотеза о применимости в данном случае законов классической механики можно обосновать огромным экспериментальным материалом, связанным с изучением движения тел вблизи поверхности Земли со скоростями много меньше скорости света. Учитывая, что высота полета мяча лежит в пределах 5—10 м, а дальность – 5—20 м, предположение о постоянстве ускорения свободного падения также представляется обоснованным. Если бы моделировалось движение баллистической ракеты при дальности и высоте полета более 100 км, то пришлось бы учитывать изменение ускорения свободного падения в зависимости от высоты и широты места.
 4-я гипотеза о движении мяча в плоскости, перпендикулярной поверхности Земли, ограничивает класс рассматриваемых траекторий и значительно упрощает модель. Траектория мяча может не лежать в одной плоскости, если при броске он сильно подкручивается вокруг вертикальной оси. В этом случае скорости точек поверхности мяча относительно воздуха на различных сторонах мяча будут различны. Для точек, движущихся навстречу потоку, относительная скорость выше, а для точек противоположной стороны, движущихся по потоку, – ниже скорости центра масс мяча. В соответствии с законом Бернулли, давление газа на поверхность больше там, где его относительная скорость меньше. Поэтому для ситуации, изображенной на рисунке, на мяч будет действовать дополнительная сила, направленная (для данной схемы) сверху вниз. Этот эффект будет проявляться тем больше, чем больше скорость центра масс мяча и скорость его вращения. Для баскетбола характерны относительно низкие скорости полета мяча (до 10 м/с). При этом довольно редко используется подкрутка мяча рукой. Поэтому гипотеза о движении мяча в одной плоскости кажется оправданной. Ее использование позволяет отказаться от построения значительно более сложной трехмерной модели движения мяча.
4-я гипотеза о движении мяча в плоскости, перпендикулярной поверхности Земли, ограничивает класс рассматриваемых траекторий и значительно упрощает модель. Траектория мяча может не лежать в одной плоскости, если при броске он сильно подкручивается вокруг вертикальной оси. В этом случае скорости точек поверхности мяча относительно воздуха на различных сторонах мяча будут различны. Для точек, движущихся навстречу потоку, относительная скорость выше, а для точек противоположной стороны, движущихся по потоку, – ниже скорости центра масс мяча. В соответствии с законом Бернулли, давление газа на поверхность больше там, где его относительная скорость меньше. Поэтому для ситуации, изображенной на рисунке, на мяч будет действовать дополнительная сила, направленная (для данной схемы) сверху вниз. Этот эффект будет проявляться тем больше, чем больше скорость центра масс мяча и скорость его вращения. Для баскетбола характерны относительно низкие скорости полета мяча (до 10 м/с). При этом довольно редко используется подкрутка мяча рукой. Поэтому гипотеза о движении мяча в одной плоскости кажется оправданной. Ее использование позволяет отказаться от построения значительно более сложной трехмерной модели движения мяча.
5-я гипотеза об отсутствии влияния сопротивления воздуха наименее обоснована. При движении тела в газе или жидкости сила сопротивления увеличивается с ростом скорости движения. Учитывая невысокие скорости движения мяча, его правильную обтекаемую форму и малые дальности бросков, указанная гипотеза может быть принята в качестве первого приближения.
Законченная концептуальная постановка позволяет сформулировать математическую постановку задачи моделирования, включающую совокупность различных математических соотношений, описывающих поведение и свойства объекта моделирования.
Контроль размерности задачи:
уравнение динамики m 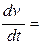 ∑ F → [кг]
∑ F → [кг] 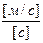 = [ H ] →
= [ H ] → 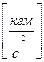 =
= 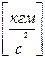 ,
,
связь скорости и перемещения  = v →
= v → 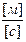 =
= 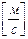 .
.
Существование и единственность решения задачи Коши доказана математиками, поэтому данную математическую модель можно считать корректной.
Для решения задачи можно использовать как аналитические, так и численные методы.
Проинтегрировав полученные соотношения по времени, получим
x (t) = C 2 + C 1 t, y (t) = C 4 + C 3 t – gt 2/2,
vx (t) = С 1, v y(t) = С 3 – gt.
Константы интегрирования находятся из начальных условий. Тогда решение задачи:
x (t) = x 0 + v 0 t cos a0, y (t) = y 0 + v 0 t sin a0 – gt 2/2,
vx (t) = v 0 cos a0, v y(t) = v 0 sin a0 – gt.
Примем, что в момент броска мяч находится в начале координат и на одном уровне с корзиной (т.е. x 0= y 0= y k=0).
Дальность L – расстояние вдоль оси 0 х от точки броска до пересечения с горизонтальной плоскостью, проходящей через кольцо корзины.
Дальность броска L = v 02 / g sin 2a0. Точность броска D = L – х к.
Проверка адекватности.
Неадекватность результатов может быть по трем причинам:
- значения задаваемых параметров не соответствует допустимой области этих параметров, определяемой принятой системой гипотез (например, силы сопротивления воздуха могут быть существенными при больших скоростях движения тела);
- константы и параметры могут быть не точными (ускорение свободного падения g может быть уточнено в зависимости от широты);
- неверна исходная совокупность гипотез.
Необходим последовательный анализ всех причин и оценка степени адекватности.
Например, отказ от учета силы сопротивления воздуха может быть грубым предположением (в зависимости от того, что считать удовлетворительной оценкой точности). Примем, что для удовлетворительной оценкой точности попадания мяча в корзину расхождение результатов моделирования и эксперимента не должно превышать 1 – 2 см.
Гипотезу об отсутствии силы сопротивления воздуха в концептуальной постановке заменим новой: сила сопротивления воздуха прямо пропорциональна скорости мяча:
F сопр = - к сопр v, где к сопр - коэффициент сопротивления, зависящий от свойств среды и формы тела.
В соотношения в математической постановке добавляются новые силы сопротивления.
Вместо соотношений m  , m
, m  - mg, вводятся новые: m
- mg, вводятся новые: m 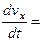 - к сопр v,
- к сопр v,
m 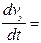 - mg - к сопр v.
- mg - к сопр v.