Этот метод по сути является аналогом метода площадей на плоскости. Его суть заключается в следующем. Объем пирамиды вычисляется по формуле 
, где S – площадь основания, h – длина высоты, проведенной к основанию пирамиды. Длина высоты пирамиды – это расстояние от вершины пирамиды до плоскости ее основания. Поэтому для вычисления расстояния от точки до плоскости достаточно найти объем и площадь основания какой-либо пирамиды с вершиной в данной точке и основанием, принадлежащим данной плоскости.
Задача 5. Дан куб 
, К – середина ребра 
. Найдите угол и расстояние между прямыми СК и 
(рис.15), если ребро куба равно 1.
Решение.
1. 
. Вычислим косинус этого угла из треугольника 
: 
, 
, 
, 
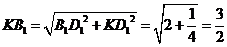. Значит, 
.
2. Расстояние между скрещивающимися прямыми СК и равно расстоянию между прямой и плоскостью 
, которая содержит прямую СК и параллельна прямой .
Вычислим расстояние от точки D до плоскости методом вспомогательного объем. Рассмотрим тетраэдр 
. Расстояние от точки D до плоскости равно высоте этого тетраэдра, проведенной из этой точки на основании тетраэдра. Значит, 
.
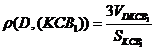Найдем объем тетраэдра.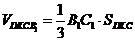 
= = 
. Вычислим площадь треугольника . 
.
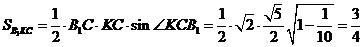Таким образом, 
. Значит, расстояние между скрещивающимися прямыми СК и равно 
Для вычисления расстояния методом вспомогательного объема часто полезным оказывается использование формулы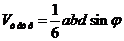 
, где а и b – длины двух скрещивающихся ребер произвольного тетраэдра, d – расстояние между ними, 
- угол между прямыми, содержащими эти ребра. Докажем это.
Дано: 
- тетраэдр (рис.16), 
= а, ВС = b, 
, 
.
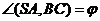Доказать: .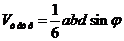
Доказательство.
1. Достроим тетраэдр до параллелепипеда следующим образом: через каждое ребра тетраэдра проведем плоскость, параллельную скрещивающимуся ребру. Получим три пары параллельных плоскостей, образующих параллелепипед. Ребра тетраэдра являются диагоналями граней полученного параллелепипеда (рис. 17).
2. Объем полученного параллелепипеда равен произведению площади параллелограмма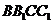 
и длины d высоты параллелепипеда, проведенной к плоскости этого параллелограмма, так как по условию расстояние между скрещивающимися прямыми SA и BC, равно d. Таким образом, 
.
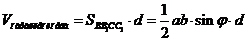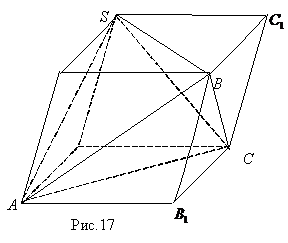3. С другой стороны, 
, где h – расстояние между плоскостями 
и 
. Найдем объем тетраэдра 
: 
.
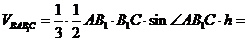
Значит, 
.
4. Так как параллелепипед состоит из данного тетраэдра и четырех равновеликих тетраэдров, объем каждого из которых равен 
объема параллелепипеда, то 
. Значит,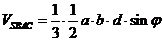 
.
Задача 6. Найти угол и расстояние между двумя скрещивающимися прямыми, содержащими медианы SМ и BN двух боковых граней правильного тетраэдра с ребром а.
Решение.
1. В плоскости 
(рис.18) проведем прямую NT параллельно SM, 
. Заметим, что Т - середина СМ, так как NT – средняя линия треугольника . Таким образом,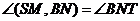 
. По тереме косинусов из треугольника 
найдем косинус этого угла. 
, 
, 
. Тогда 
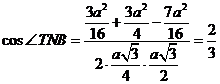, и 
.
2. Для вычисления расстояния между прямыми SМ и BN вычислим объем тетраэдра SMBN двумя способами.
С одной стороны, 
, 
, так как у тетраэдров SMBC и NMBC – общее основание, а высоты относятся как 2:1. Следовательно, 
.
С другой стороны, 
, где d – расстояние между SМ и BN, 
. Тогда 
.
Следовательно, 
.
Таким образом, угол между прямыми SМ и BN равен 
, а расстояние – 
.