f(x)=f(x0+  x)
x)  f(x0)+f, (x0)∆x – это означает линеаризацию ф-ции у=f(x), т.е. ее замену линейной по х ф-цией у=f(x0)+f, (x0)(x-x0), что гометрически соответствует замене участка кривой у=f(x), примыкающего к точке (х0;f(x0)), отрезком касательной к кривой в этой точке.
f(x0)+f, (x0)∆x – это означает линеаризацию ф-ции у=f(x), т.е. ее замену линейной по х ф-цией у=f(x0)+f, (x0)(x-x0), что гометрически соответствует замене участка кривой у=f(x), примыкающего к точке (х0;f(x0)), отрезком касательной к кривой в этой точке.
№26
Пусть дифференцируемая ф-ция у=f(x) определена в некоторой окрестности и во внутренней точке данной окрестности имеет локальный экстремум. Тогда производная в этой точке равна нулю.
№18
Если ф-цииv=v(x) и u=u(x) имеют производные в точке х0, то сумма(разность, произведение, частное) этих ф-ций имеют производные в точке х0, при условии, что v (x0)  .
.
Тогда справедливы равенства:
1. Производ. суммы/разн-ти 2х ф-ций = сумме/разности производных этих ф-ций.
2. Производная произведения 2х ф-ций = сумме произведений производной первой ф-ции на вторую и производной второй ф-ции на первую.
3. Производная частного 2х ф-ций = дроби, знаменатель которой равен квадрату делителя, а числитель – разности произведения производной делимого на делитель и производной делителя на делимое.
Логарифмическое дифференцирование: Исследуем.ф-ция вначале логарифмир-ся по основанию е: lny=ln(f(x)). Затем ф-циядифференцир-тся по х, помня, что у явл-ся сложной ф-цией от х. Затем выражаем у, из получен.соотнош. Данный метод примен-ся, если задан.ф-ция представ. Собой произвед. многих ф-ций или явл. частным таких произвед.; или при отыскании производной степенно-показательной ф-ции.
№23
Производная сложной ф-ции: у,х= у ,u  u,x
u,x
Производная обратной ф-ции:  , у =1/у,х
, у =1/у,х
Логарифмическое дифференцирование: Исследуемая ф-ция вначале логарифмируется по основанию е:lny=ln(f(x)). Затем ф-ция дифференцируется по х, помня, что у является сложной ф-цией от х. Затем выражаем  из полученного соотношения. Данный метод применяется если заданная ф-ция представ. Собой произведение многих ф-ций или явл. частным таких произведений; или при отыскании производной степенно-показательной ф-ции.
из полученного соотношения. Данный метод применяется если заданная ф-ция представ. Собой произведение многих ф-ций или явл. частным таких произведений; или при отыскании производной степенно-показательной ф-ции.
№24
Т. к. дифференциалы получаем из производной умножением на дифференциал независимой переменной, зная таблицу производных, получаем:

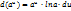 и т.д.
и т.д.
В соответствии с правилами дифференцирования производных получаем следующее правило для дифференциалов: d(u+v)=du+dv
d(uv)=vdu+udv
d(u/v)=vdu-udv/v2 и т.д.
Свойство инвариантности
Рассмотрим функцию y = f(u), где u = f (x), то есть рассмотрим сложную функцию y = f(f(x)). Если каждая из функций f и f являются дифференцируемыми, то производная сложной функции равна y' = f'(u)· u'. Тогда дифференциал функции
dy = f'(x)dx = f'(u)u'dx = f'(u)du,
так как u'dx = du. Т.е. dy = f'(u)du.
Последнее рав-во означает, что формула дифференциала не изменяется, если вместо фун-и от x рассматривать фун-ю от переменной u. Это свойство дифференциала получило название инвариантности формы первого дифференциала.
№22
Дифференцирование неявно заданных ф-ций: 1) продифференцировать обе части равенства F(x;y)=0 по переменной х, считая, что у=у(х). 2)Из получившегося в результате дифференцирования равенства выразить у ,х через х и у.
Если ф-ция задана параметрически 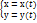 , то производные вычисляются по формулам у ,х =у ,t/ x, t
, то производные вычисляются по формулам у ,х =у ,t/ x, t
y,,xx =(y,x) , t/x, t
№35
Точки наиб.инаим. значений ф-ции на некотором мн-ве Х (на отрезке) называются точками глобального экстремума ф-ции на этом мн-ве.Ф-ция, непрерывная на отрезке, достиг.своего наиб. и наим. значений на этом отрезке или а его концах.
Правило нахождения наиб.инаим. значений ф-ции на отрезке [a;b]:
Находим и приравниваем к нулю производную ф-ции, выражаем х
Находим критические точки ф-ции у=f(x), принадлежащие интервалу (а;b)
Вычисляем значения ф-ции в критической точке и на концах отрезка
Из найденных значений выбираем наибольшее и наименьшее
№40
Х2+1=0
Х2=-1
i –мнимая единица, i2= -1 -i – сопряженное мнимой единице.
Под множеством комплексных чисел понимаем упорядоченное мн-во пар действительных чисел, над которыми можно выполнить след.действия:
(a,b)=(c,d) 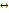 a=c, b=d
a=c, b=d
(a,b)  (c,d)
(c,d) 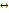 (a
(a  c, b
c, b  d)
d)
(a,b)  (c,d)
(c,d) 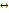 (ac-bd, ad+bc)
(ac-bd, ad+bc)
(a,b):(c,d)  ; =
; = 
Множество комплексных чисел обозначается С
Формула Муавра: zn= rn(cosn  +isinn
+isinn  )
)
№34
Первый достаточный признак экстремума
Пусть ф-ция у=f(x) непрерывна в точке х0 и дифференцируема в некоторой ее окрестности. Если при переходе слева направо через точку х0 производная меняет знак с – на +, то х0 – точка строго минимума; если знак меняется с + на -, то точка х0 – точка строгого максимума.
Второй достаточный признак экстремума:
Пусть ф-ция у=f(x) имеет в точке х0 равную нулю первую производную и непрерывную отличную от нуля вторую производную. Тогда если 
Исследование на экстремум с помощью второй производной:
Найти первую производную и точки, в которых она равна нулю.(стационарные точки)
Найти вторую производную и определить ее знак в каждой стационарной точке. Если производная в точке х0<0, то х0 – точка строгого максимума, если >0,то х0 – точка строгого минимума.
№3
Если каждому элементу х из мн-ва Х поставлен в соответсвие (по некоторому правилу f) единственный элемент у из мн-ва У, то говорят, что задано отображениемн-ва Х в мн-во У.
(f:X 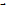 Y). Х – множество определения и обозначается Df, Y – множество значений и обозначается Ef.
Y). Х – множество определения и обозначается Df, Y – множество значений и обозначается Ef.
Сложная функция – функция от функции. Если z – функция от у, т.е. z(y), а у, в свою очередь, – функция от х, т.е. у(х), то функция f(x) = z(y(x)) называется сложной функцией (или композицией, или суперпозицией функций) от х.
В такой функции х – независимая, а у – промежуточная переменная. При этом сложная функция определена для тех значений независимой переменной, для которых значения промежуточной функции у входят в область определения функции z(y).
Обратная функция
Если поменять ролями аргумент и функцию, то x станет функцией от y. В этом случае говорят о новой функции, называемой обратной функцией. Предположим, мы имеем функцию:v = u2, где u - аргумент, a v - функция. Если поменять их ролями, то мы получим u как функцию v: u = 
Под ф-цией понимаем отображение числовых множеств.
Графиком ф-ции является множество всех точек (х;у) плоскости Оху, для каждой из которой значение аргумента х явл. абсциссой, а значение у=у(х) ф-ции – ординатой.
№4
Окрестностью точки а  (конечной точки) называется любой интервал, содержащий эту точку.
(конечной точки) называется любой интервал, содержащий эту точку.
 .
.
Число b называется пределом ф-ции у=f(x) приx 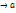 , если для любой окрестности В(b) точки b найдется такая проколотая окрестность
, если для любой окрестности В(b) точки b найдется такая проколотая окрестность  точки а, что как только x
точки а, что как только x  (а), то f(x)
(а), то f(x)  B(b), что обозначается b=
B(b), что обозначается b=  .
.
№25
Производные высших порядков
Производной второго порядка ф-цииу=f(x) наз. производная от производной f, (x): f,, (x)=(f, (x)),
Производной n-го порядка назыв. производная от производной (n-1)-го порядка:
f(n) (x) = (f(n-1)(x)),, n=1,2…
Дифференциал от дифференциала ф-ции у=f(x) наз. дифференциалом второго порядка. Дифференциалом n-го порядка наз. дифференциал от дифференциала (n-1)-го порядка, n=2,3…
d2y=f ,, (x0) dx2, dny=f (n)(x0)dxn
№21

(sh x), = ch x (ch x) , = sh x
th x=  (th x),=1/ch2cth x=
(th x),=1/ch2cth x= 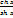 (cth x) , = - 1/sh2
(cth x) , = - 1/sh2
№30

где Rn(x) - остаточный член формулы Тейлора.
В форме Лагранжа 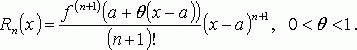
В форме Пеано
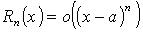
№4 Окрестностью точки а ∈R(конечнойточки) называетсялюбойинтервал, содержащийэтуточку.
Число b называется пределом ф-ции у=f(x) при x→a, если для любой окрестности В(b) точки b найдется такая проколотая окрестность  (а) точки а, что как только x∈
(а) точки а, что как только x∈  (а), то f(x)∈B(b), чтообозначается b=
(а), то f(x)∈B(b), чтообозначается b=  .
.
Существуют конечные пределы в конечной точке, конечные пределы на бесконечности, бесконечные пределы в конечной точке, бесконечные пределы на бесконечности, односторонние пределы.
№5
Число b называется пределом ф-ции у=f(x) при х  а, если для любого сколь угодно малого
а, если для любого сколь угодно малого 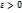 найдется такое число
найдется такое число 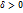 , что для всех х, удовлетв. условию lx – al<δ, х
, что для всех х, удовлетв. условию lx – al<δ, х  а, будет выполняться неравенствоIf(x) – bI<ε.
а, будет выполняться неравенствоIf(x) – bI<ε.
№6 Конечное число а называется пределом числовой последовательности {xn}, если для любого сколь угодно малого числа ε найдется такое натуральное число n0(ε), что все члены этой последовательности с номерами n>n0(ε) удовлетворяют неравенству Ixn – aI<ε.В этом случае пишут  и говорят, что последовательность {xn} имеет предел а.
и говорят, что последовательность {xn} имеет предел а.
№17
Если ф-ция дифференцируема в данной точке, то она непрерывна в ней. Но если ф-ция непрерывна в точке, то она может быть не дифференцируемой в этой точке.
№32
Чтобы дифференцируемая на интервале (a;b) ф-ция у= f(x) не убывала/ не возрастала на этом интервале, необходимо и достаточно, чтобы ее производная была во всех точках интервала неотрицательной,т.е. f,(x)  /неположительной, т.е. f ,(x)
/неположительной, т.е. f ,(x)  0
0