Устойчивым методом называем метод, при использовании которого решение меняется мало при малых изменениях входных данных.
Соответственно, метод решения, при использовании которого малые возмущения входных данных, например, ошибки округления, приводят к сильному изменению результатов расчетов, назовем неустойчивым методом.
Численная устойчивость означает непрерывную зависимость решения от входных данных.
Будем рассматривать устойчивость методов на примере решения уравнения
, (9.21)
которое назовем тестовым уравнением. Решение уравнения (9.21) представляет собой затухающую экспоненту. Например, при начальном условии
(9.22)
точное решение равно 
. Будем считать метод решения уравнения (9.21) устойчивым, если он описывает затухающую экспоненту.
Пример 9.5. Решим задачу Коши для тестового уравнения (9.21), (9.22) методом Эйлера:
.
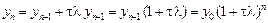Решение Эйлера описывает экспоненциально затухающую функцию, если
. (9.23)
Если значение t выходит за пределы, указанные неравенствами (9.23), то не просто падает точность, а принципиально меняется характер решения. В то же время решение Эйлера устойчиво, если выполнены условии (9.23). Ранее уже говорилось, что ломаная Эйлера стремится к истинной интегральной кривой, если шаг приращения аргумента стремится к нулю. Заключаем отсюда, что метод Эйлера устойчив при выполнении ограничений на выбор шага приращения аргумента.
Метод Эйлера является одношаговым методом. Рассмотрим теперь примеры многошаговых методов.
Пример 9.6. Решим ту же задачу Коши (9.21), (9.22) двухшаговым методом третьего порядка:
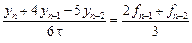. (9.24)
Подставим в формулу (9.24) 
и разрешим полученное выражение относительно 
. Решение в среде Mathcad приведено на рис. 9.4. Для решения двухшаговым методом дополнительно добавляем условие 
– значение точного решения в точке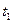 
. Решение представлено в матрице М:
- первый столбец дает значения аргумента;
- второй – точное решение;
- третий – приближенное решение.
Видим, что, начиная с некоторого шага, приближенное решение резко отличается от точного. Легко убедиться, что расхождение наблюдается и при уменьшении шага приращения аргумента. Заключаем, что метод является неустойчивым.
Пример 9.7.
Решим задачу Коши для тестового уравнения (9.21), (9.22) неявным двухшаговым методом третьего порядка:
. 9.25)
Подставив сюда и разрешив уравнение относительно , получим:
.
Решение в среде Mathcad приведено на рис. 9.5. Как и в предыдущем примере, решение представлено в матрице М:
- первый столбец дает значения аргумента;
- второй – точное решение;
- третий – приближенное решение.
Видим, что приближенное решение совпадает с точным по меньшей мере в пределах трех значащих цифр. Легко убедиться, что характер приближенного решения остается тем же и при увеличении шага приращения аргумента. Заключаем, что данный метод является устойчивым.
Из рассмотренных примеров следует, что не все разностные методы пригодны для решения дифференциальных уравнений.
Для обнаружения неустойчивости метода
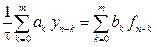(9.26)
достаточно рассмотреть левую часть уравнения (9.26), т.е. однородное разностное уравнение
. (9.27)
Ищем решение этого уравнения в виде
. (9.28)
Подставив это решение в уравнение (9.27) и сократив лишние сомножители, получим алгебраическое уравнение, которое называют характеристическим уравнением разностного метода:
. (9.29)
Очевидно, что если q – корень характеристического уравнения, то есть частное решение однородного разностного уравнения (9.27). Общее решение разностного уравнения представляет собой взвешенную сумму частных решений. Если все корни характеристического уравнения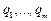 
различны, то общее решение уравнения (9.27) равно сумме
, (9.30)
где A k – постоянные, определяемые из начальных условий. Если среди корней характеристического уравнения есть кратный корень q i кратности s, то линейно независимыми решениями разностного уравнения (9.27), соответствующими этому корню, являются функции:
. (9.31)
Собственные решения однородного уравнения (9.27) – это собственные решения разностного метода, существующие независимого от того, какое дифференциальное уравнение мы решаем. Характер собственных решений метода проявляется при решении дифференциального уравнения. Общее решение неоднородного ур-я
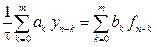
есть сумма какого-либо его частного решения и общего решения соответствующего однородного уравнения. Если среди собственных решений есть безгранично нарастающие, то метод вносит сильные искажения в решение дифференциального уравнения и оказывается фактически непригодным – оказывается неустойчивым.
Пример 9.8.
Вернемся еще раз к примеру 9.6 – решение тестового уравнения
,
с помощью двухшагового метода:
.
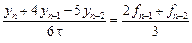Характеристическое уравнение для однородного разностного уравнения
(9.32)
имеет вид:
.
Решение характеристического уравнения:
.
Соответственно решение однородного уравнения (9.32) включает две компоненты: константу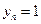 
и быстро растущую компоненту 
.
Однородное разностное уравнение всегда имеет тривиальное решение – это решение с нулевыми начальными условиями. Однако для неустойчивого метода даже незначительные возмущения нулевых начальных условий вызывают безграничный рост решения разностного уравнения. На рис. 9.6 показано решение уравнения (9.32) для случая малых начальных условий. Видим, что решение быстро растет.
 |
Наличие безгранично растущего собственного решения разностного метода искажает решение дифференциального уравнения и делает метод непригодным.
Пример 9.9.
Найдем собственные решения для неявного разностного метода
.
Однородное уравнение имеет вид:
.
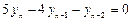Решения характеристического уравнения 
равны: 
, и среди собственных решений разностного метода нет безгранично нарастающих.
Условие корней:
Разностный метод удовлетворяет условию корней, если все корни характеристического уравнения 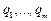лежат внутри или на границе единичного круга комплексной плоскости, причем на границе круга нет кратных корней.
Пример 9.10.
Проверим, удовлетворяет ли условию корней метод Милна 
.
Характеристическое уравнение метода имеет вид:
.
Оба корня уравнения 
лежат на единичной окружности, но не являются кратными, следовательно, метод Милна удовлетворяет условию корней.
Замечание 1:
Выполнение условия корней не гарантирует, что метод сходится при любом значении шага приращения аргумента.
Замечании 2:
всегда является корнем характеристического уравнения
.
Это следует из уравнения для коэффициентов метода: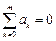 
.
Замечании 3. Все методы Адамса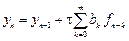 
удовлетворяют условию корней, т.к. характеристическое уравнение методов 
имеет всего один корень .
Утверждения.
Для устойчивых методов порядок аппроксимации удовлетворяет неравенству
Для явных m -шаговых устойчивых методов порядок аппроксимации не превосходит m.
Вопросы для повторения
- Формула линейного разностного m -шагового метода общего вида. Формула метода Адамса.
- Достоинства и недостатки многошаговых методов. Достоинства и недостатки неявных методов.
- Метод предиктор-корректор.
- Порядок явного и неявного m -шагового метода общего вида. Порядок метода Адамса.
- Характеристическое уравнение m -шагового метода.
- Условие корней для линейного разностного m -шагового метода. Что гарантирует выполнение условия корней? Выполняется ли условие корней для методов Адамса?