Лекция 2.
Повторные независимые испытаний
План лекции.
1.Формула полной вероятности.
2.Формула Бейеса.
3.Повторение испытаний.
4. Формула Бернулли. Наивероятнейшее число появлений событий.
5.Локальная и интегральная формулы Лапласа.
6.Вероятность отклонения относительной частоты от постоянной вероятности.
7. Теорема Пуассона.
Литература: [1], [2], [3], [4].
Формула полной вероятности
Пусть событие А может наступить при условии появления одного из несовместных событий 
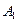 ,
, 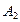 ,…,
,…,  , которые образуют полную группу событий. Пусть известны вероятности этих событий и условные вероятности события А.
, которые образуют полную группу событий. Пусть известны вероятности этих событий и условные вероятности события А.
Теорема. Вероятность появления события А, которое может наступить лишь при появлении одного из несовместных событий 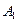 ,
, 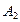 ,…,
,…,  , образующих полную группу событий, равна сумме произведений вероятностей каждого из этих событий на соответсвующую вероятность события А:
, образующих полную группу событий, равна сумме произведений вероятностей каждого из этих событий на соответсвующую вероятность события А:
Р(А) = Р (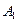 )
) 
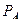 (А) + Р (
(А) + Р (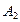 )
) 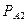 (А) + Р (
(А) + Р ( )
) 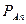 (А).
(А).
Полученная формула называется формулой полной вероятности.
Формулы Бейеса
Пусть событие А может наступить при условии появления одного из несовместных событий 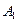 ,
, 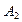 ,…,
,…,  , образующих полную группу событий. Посколько заранее не известно, какое из этих событий наступит, их называют гипотезами. Вероятность появления события А определяется по формуле полной вероятности.
, образующих полную группу событий. Посколько заранее не известно, какое из этих событий наступит, их называют гипотезами. Вероятность появления события А определяется по формуле полной вероятности.
Допустим далее, что произведено испытание, в результате которого появилось событие А. Поставим своей задачей определить, как изменились вероятности  гипотез. Другими словами будем искать условные вероятности
гипотез. Другими словами будем искать условные вероятности 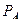 (
(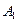 ),
), 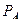 (
(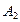 .),…,
.),…, 
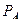 (
( ).
).
Найдем сначала условную вероятность 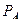 (
(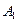 ). По теореме умножения имеем:
). По теореме умножения имеем:
Р (А 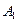 ) = Р (А)
) = Р (А) 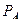 (
(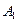 ) = Р (
) = Р (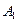 )
) 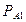 (А).
(А).
Отсюда
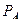 (
(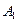 )= Р(
)= Р(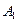 )
) 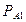 (А)/ Р(А).- формулы Бейеса.
(А)/ Р(А).- формулы Бейеса.
Аналогично выводятся формулы для определения условных верояостей других гипотез.
Формулы гипотез позволяют переоценить вероятности гипотез после того как становится известным результат испытания, в итоге которого появилось событие А.
Повторение испытаний.
Пусть производится серия из n независимых испытаний, в каждом из которых событие А может появиться или нет, причем появления события А при каждом испытании постоянна и равна р, а вероятность не появления события А равна q= 1-p.
Тогда вероятность того, что событие А в этой серии произойдет ровно m раз, определяется по формуле Бернулли (формуле биноминального распределения):
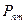 =
= 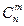
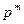
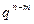
Пример. Вероятность того, что автомат данного типа потребует вмешательство оператора в течении часа равна 0,3. Какова вероятность того, что в течении часа вмешательство оператора потребуют два автомата из пяти работающих?
Решение. В нашем случае, p = 0,3, q = 1- 0,3 =0,7, n =5, m =2
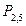 =
= 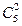

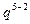 =
= 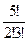
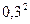
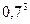 =10* 0,09*0,343 = 0,3087.
=10* 0,09*0,343 = 0,3087.
Формулу Бернулли целесообразно применять в случаях, когда n не очень велико.
При больших значениях n использовать формулу Бернулли практически невозможно Поэтому важны приближенные формулы, достаточно простые и точные.
Локальная теорема Муавра – Лапласа
В случае, если число испытаний п велико, а вероятность появления события А постоянна и отлична от нуля, то вероятность того, что событие А в серии из n испытаний произойдет ровно m раз приближенна равна значению функции 
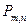 =
= 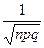 f(х), где f(х) =
f(х), где f(х) = 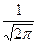



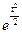 , t =
, t = 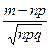 ,
,
где функция f(х)- табулированная функция., четная.Эта формула дает результат достаточной точности, если выполнено условие 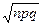
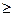 15.
15.
Формула Пуассона (формула малых вероятностей)
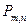 =
= 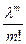 e
e 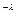 ,
, 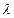 = np.
= np.
Вероятностный смысл 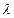 - это среднее число появления события А в испытаниях.
- это среднее число появления события А в испытаниях.
Значения функции Пуассона для различных 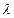 и
и  приведены в таблицах. Формула обеспечивает достаточно высокую точность при выполнении условий n
приведены в таблицах. Формула обеспечивает достаточно высокую точность при выполнении условий n 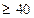 ,
, 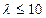 .
.
Если вероятность наступления события А в п независимых испытаниях постоянна и равна р и отлична от 0 и 1, то вероятность того, что событие А появится в п испытаниях не менее 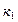 раз, но не более
раз, но не более 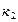 раз приближенно вычисляется по интегральной теореме Лапласа:
раз приближенно вычисляется по интегральной теореме Лапласа:
Р (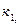 ,
, 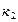 ) =
) = 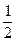 (Ф(
(Ф(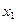 )-Ф(
)-Ф(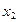 )), Ф(х)=
)), Ф(х)= 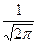
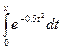 ,
,
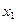 =
= 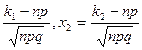
Значения функции Ф(х) табулированы для различных х. При пользовании таблицей следует учитывать, что эта функция нечетная. Достаточная точность формулы обеспечивается при условии 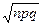
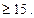
Пример. Найти вероятность того, что соб  ытие А наступит ровно 80 раз в 400 испытаниях, если вероятность появления этого события к в каждом испытании равна 0,2.
ытие А наступит ровно 80 раз в 400 испытаниях, если вероятность появления этого события к в каждом испытании равна 0,2.
Решение. По условию п=400, к=80,р=0,2.
Воспользуемся асимптотической формулой Лапласа:
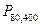 =
= 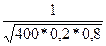
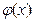 =
= 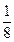
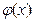 .
.
Вычислим определяемое данными значение х: х= 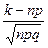 =
= 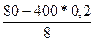 =0
=0
По таблице находим 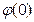 =0,3989. Искомая вероятность
=0,3989. Искомая вероятность 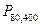 =
= 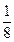 *0,3989= 0,04986.
*0,3989= 0,04986.
Пример. Вероятность поломки одной дорожной балки 0,1. Найти вероятность того,что из 100 балок сломаются не более 15.
Решение. P=0,1, q=0,9, 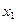 =
= 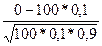 =-3,3333
=-3,3333
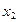 =
= 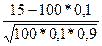 =1,667,Ф(3,3333)=-Ф(3,3333)= -0,4995, Ф(1,667)= 0,4526
=1,667,Ф(3,3333)=-Ф(3,3333)= -0,4995, Ф(1,667)= 0,4526
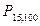 =0,4526+ 0,4995= 0,9521.
=0,4526+ 0,4995= 0,9521.
Пример. Вероятность того,что на базу прибудет неисправный товар 0,003. Найти вероятность того, что на базу придет 4 неисправных товара из 100.
Решение. P=0,003, 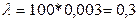 .
. 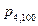 =
=  =0,00002.
=0,00002.