Лекция
Тема: Основные понятия: множества, их элементы и подмножества. Операции над множествами. Взаимно-однозначное соответствие. Мощность конечных и бесконечных множеств. Отношения и функции.
Теория множеств — раздел математики, в котором изучаются общие свойства множеств. Теория множеств лежит в основе большинства математических дисциплин; она оказала глубокое влияние на понимание предмета самой математики. «Множества» окружают нас повсюду. Люди, студенты, звезды, понятия — все эти предметы, мыслимые вместе, образуют множества. Коллектив, созвездие, полк — это тоже множества людей или звезд.
Таким образом, любые объекты, которые мы мыслим вместе и которые мы можем объединить либо списком, либо при помощи общего признака, будут составлять множество. Несмотря на основополагающий характер данной теории и достаточную давность ее исследования, в этой области существует большое количество неточностей, противоречий и парадоксов. В настоящее время теория множеств широко используется при решении задач на компьютере.
Она значительно облегчает запись на различных языках программирования. Рассмотрение теории множеств дает ключ к дальнейшему более глубокому понимаю всех отраслей математики.
До второй половины 19-го века понятие "множества" не рассматривалось в качестве математического ("множество книг на полке", "множество человеческих добродетелей" и т. д всё это чисто бытовые обороты речи). Положение изменилось, когда немецкий математик Георг Кантор разработал свою программу стандартизации математики, в рамках которой любой математический объект должен был оказываться тем или иным "множеством".
Понятие множества, элементы множества – первичные базисные неопределяемые понятия, на которых строится теория множеств. Понятие множества нельзя свести к каким-то более простым математическим объектам, но можно пояснить с помощью наглядных примеров.
Язык теории множеств.
Множество – это совокупность элементов, объединенных некоторым признаком, свойством: множество книг в библиотеке, множество студентов в группе.
Способы задания множества:
- Перечислить все его элементы.
Например: множество, состоящее из четырех элементов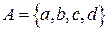 
.
- Указать свойство, которым обладают все его элементы.
Например: множество натуральных чисел, меньших 20 можно задать следующим образом: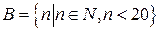 
.
В качестве характеристического свойства может выступать порождающая процедура, которая описывает способ получения элементов множества из уже полученных элементов или из других объектов.
Например: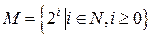 
Если элемент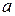 
принадлежит множеству 
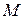, используют запись 
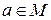, если не принадлежит, то 
.
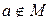Во множестве могут быть выделены подмножества. Если каждый элемент множества K принадлежит множеству М, множество К называют подмножеством множества М и обозначают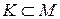 
.
Например:
1) множество всех книг данного автора в библиотеке, есть подмножество всех книг в библиотеке.
2) множество студентов, обучающихся на "4" и "5" в группе есть подмножество всех студентов группы.
3) 
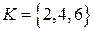четных чисел меньших или равных 6, есть подмножество множества 
.
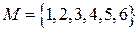Пустое множество является подмножеством любого множества.
Если одновременно А ⊂ В и В ⊂ А, то говорят, что множества А и В равны, т.е. состоят из одних и тех же элементов. В этом случае принадлежность элемента множеству А необходима и достаточна для его принадлежности множеству В.
Булеаном множества М назовем множество всех его подмножеств.
Пример: Рассмотрим множество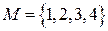 
. Составим все подмножества множества М.
, 
, 
, 
, 
, 
, 
, 
, 
,
, 
, 
, 
,
.
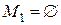
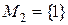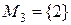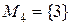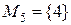
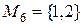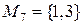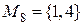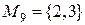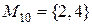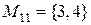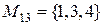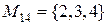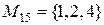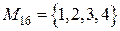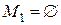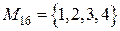Подмножества и являются несобственными подмножествами множества М, остальные – собственные подмножества. Всего мы нашли 16 различных подмножеств множества М. Это число равно 
.
В общем случае, для любого конечного множества, состоящего из n элементов, число возможных подмножеств равно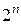 
.
Множество U, состоящее из всех возможных элементов, обладающих данным признаком, называется универсальным.
Классификация множеств.
Основной характеристикой множеств является количество элементов, содержащихся в этом множестве.
Множество, содержащее конечное число элементов называется конечным. Множество, не являющееся конечным, называется бесконечным. Количество элементов конечного множества называют его мощностью. Если множество не содержит элементов, то оно называется пустым и обозначается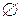 
.
Два множества А и В называются эквивалентными, или, равномощными, если между их элементами можно установить взаимно-однозначное соответствие.
Пример: Рассмотрим множества, состоящие из букв слов:
; 
; 
; 
.
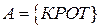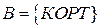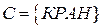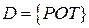Множества А, В и С имеют равные мощности: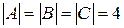 
, а мощность множества D меньше 
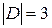. При этом множества А и В равны, а множества А и С – эквивалентны.
Эталоном для сравнения множеств служит натуральный ряд чисел. Поэтому все числовые последовательности, содержащие различные элементы, эквивалентны натуральному ряду чисел, что видно по их индексам.
Бесконечное множество, эквивалентное множеству натуральных чисел, называется счетным. Говорят, что все элементы счетного множества пронумерованы. В противном случае бесконечное множество будет несчетным. В 1878 году Георг Кантор доказал, что множество точек расположенных на отрезке от 0 до 1 несчетно.
Изображение множеств.
Множества изображаются при помощи диаграмм Эйлера-Венна (кругов на плоскости). Элементы множества изображаются точками, внутри круга, если они принадлежат данному множеству и вне его, если не принадлежат.
, 
. 
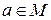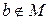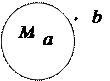
1.4. Операции над множествами.
Основными операциями над множествами являются операции пересечение, объединение, разность, симметрическая разность и дополнение.
1. Пересечением множеств А и В называется множество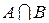 
, состоящее из элементов, которые принадлежат одновременно как множеству А так и множеству В.
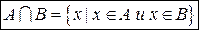
Пример: Если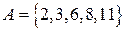 
, 
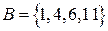, то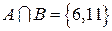 
.
При помощи диаграмм Эйлера-Венна пересечение множеств изображается следующим образом:
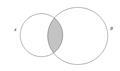
2. Объединением множеств А и В называется множество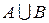 
, состоящее из элементов, которые принадлежат или множеству А или множеству В.
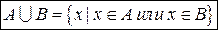
Пример: Если 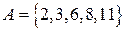, , 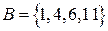то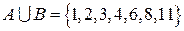 
.
При помощи диаграмм Эйлера-Венна объединение множеств изображается следующим образом:
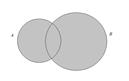
3. Разностью множеств А и В называется множество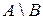 
, состоящее из элементов множества А, которые не принадлежат множеству В.
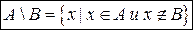
Пример: Если 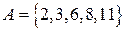, , 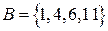то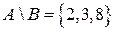 
.
При помощи диаграмм Эйлера-Венна разность множеств изображается следующим образом:
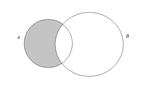
По диаграмме видно, что 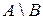можно заменить на 
.
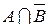4. Симметрической разностью А и В называется множество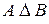 
, состоящее из элементов множеств А или В, но не принадлежащих этим множествам одновременно.
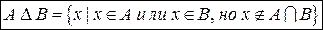
Пример: Если 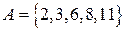, , 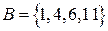то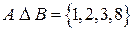 
.
При помощи диаграмм Эйлера-Венна симметрическая разность множеств изображается следующим образом:
5. Дополнением множества А до множества U называется множество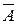 
, состоящее из элементов множества U, которые не принадлежат множеству А.
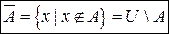
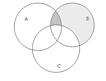
При помощи диаграмм Эйлера-Венна дополнение множества изображается следующим образом:
Свойства операций.
Операции над множествами обладают рядом свойств, похожих на свойства операций сложения и умножения чисел.
| Объединение (сложение) | Пересечение (умножение) |
| 1. Коммутативность (переместительное свойство) | |
| 
|
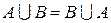
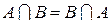
| 2. Ассоциативность (сочетательное свойство) | |
| 
|
| |
| |
| |
| |
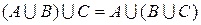
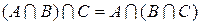
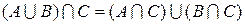
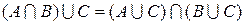
| 5. Закон поглощения | |
| 
|
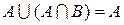
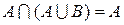
| 6. закон де Моргана | |
| 
|
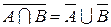
| 7. закон склеивания | |
| 
|
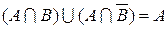
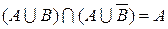
| 8. закон Порецкого | |
| 
|
 , 
|  , 
|
 , 
|  , 
|
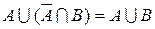
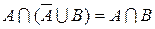
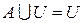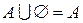
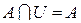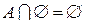
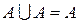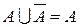
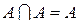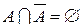
Используя эти операции можно выражать одни множества через другие, при этом сначала выполняется операция дополнения, затем пересечения и только затем операции объединения и разности. Для изменения порядка в выражении используют скобки.
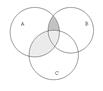
Пример. Доказать справедливость следующего равенства и проверить результат на диаграмме Эйлера-Венна: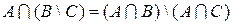 
.
Решение. Преобразуем по очереди левую и правую части данного равенства:
1) 
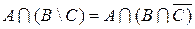. Заменили разность на пересечение с дополнением.
2) 
.
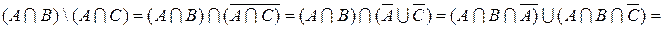
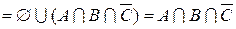Использовали переход от разности к пересечению, закон де Моргана, свойство дистрибутивности, свойство 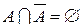и .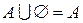
После преобразования видно, что левая и правая части равенств одинаковые, следовательно, равенство доказано.
Проверим равенство на диаграмме Эйлера-Венна.
Формула включений и исключений.
Найдем сколько элементов содержится в множестве А ∪ В. Основная формула нахождения числа элементов суммы двух множеств
n (А ∪ В) = n (А) + n (В) – n (А ∩ В).
Действительно, n (А ∪ В) — это сумма числа элементов множеств А и В, но при подсчете элементы, принадлежащие А ∩ В учитывались дважды. С помощью данной формулы можно получить формулы для определения числа элементов суммы любого числа множеств. Например для трих множеств она выглядит следующим образом:
n (А ∪ В ∪ С) = n (А) + n (В) + n (С) – n (А ∩ В) – n (В ∩ С) – n (А ∩ C) + n (А ∩ В ∩ С).
Данная формула используется для решения различных задач.
Пример. Из 100 школьников английский знают 42, немецкий — 30, французский — 28, английский и немецкий — 5, английский и французский — 10, немецкий и французский — 8, английский, немецкий и французский — 3 школьника. Сколько школьников не знают ни одного языка?
Решение.
Обозначим через А — множество школьников, знающих анг-ийский язык; N — множество школьников, знающих немецкий язык; F — множество школьников, знающих французский язык.
Тогда n (A) = 42, n (N) = 30, n (F) = 28, n (A ∩ N) = 5,
n (A ∩ F) = 10, n (N ∩ F) = 8, n (A ∩ N ∩ F) = 3.
Найдем с помощью формулы включений и исключений количество школьников, знающих хотя бы один из перечисленных иностранных языков.
n (A ∪ N ∪ F) = n (A) + n (N) + n (F) =
= n (A ∩ N) – n (A ∩ F) – n (N ∩ F) + n (A ∩ N ∩ F) =
= 42 + 30 + 28 – 5 – 10 – 8 + 3 = 80.
Следовательно, не знают ни одного иностранного языка: 100 – 80 = 20 школьников.
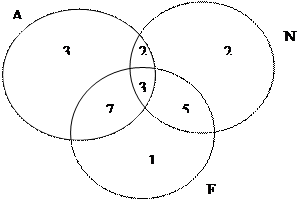
Эту же задачу можно решить с помощью диаграммы Эйлера–Венна
Так как 3 языка знают 3 школьника, то английский и немецкий знают 5 – 3 = 2, английский и французский — 10 – 3 = 7,
немецкий и французский — 8 – 3 = 5 школьников.
Только английский знают 42 – (2 + 3 + 7) = 30, только немецкий — 30 – (2 + 3 + 5) = 20,
только французский — 28 – (3 + 5 + 7) = 13 школьников.
Ни одного языка не знают 100 – (2 + 3 + 5 + 7 + 13 + 20 + 30) = 20 школьников.
 |
Бинарные отношения.
Основные понятия.
Исследователя окружающего мира интересуют различные свойства объектов: свойства, относящиеся к отдельным объектам (например, "быть женщиной", "иметь форму правильного пятиугольника", "быть сделанным из металла", "быть зеленым", "иметь низкую теплопроводность") и свойства, характеризующие связи между несколькими объектами (например, свойства "быть родственниками" и "быть больше" относятся к парам объектов, свойство "находиться между" - к тройкам объектов, свойство "располагаться в вершинах квадрата" - к четверкам объектов). Такие свойства принято называть отношениями. При этом свойства отдельных объектов называются унарными отношениями, свойства, относящиеся к парам объектов, - бинарными отношениями, свойства, относящиеся к наборам из n объектов, - n-арными отношениями. Ниже мы ограничимся рассмотрением лишь бинарных отношений.
Бинарные отношения служат простым и удобным аппаратом для весьма широкого круга задач. Язык бинарных и n- арных отношений используется во многих прикладных (для математики) областях, например, таких как математическая лингвистика, математическая биология, математическая теория баз данных. Широкое использование языка бинарных отношений легко объясняется - геометрический аспект теории бинарных отношений есть попросту теория графов.
Кортежи.
Пусть А – конечное множество, состоящее из n элементов, f: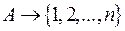 
- функция, задающая порядок на А, т.е. правило, по которому каждому элементу множества А ставится в соответствие натуральное число от 1 до n, причем одному числу из 
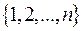соответствует один элемент из А.
Пару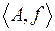 
назовем упорядоченным множеством, или перестановкой, из n элементов.
Кортежем длины n из элементов множества А называется упорядоченная последовательность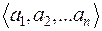 
элементов этого множества.
Пусть А – конечное множество, элементами которого являются некоторые символы, например цифры, буквы, знаки препинания. Такие множества принято называть алфавитом над заданным множеством. Алфавит есть кортеж попарно различимых символов, называемых буквами алфавита. Элементы множества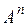 
принято называть словами длины n.
Например. Шестизначный телефонный номер является словом длины 6 над алфавитом цифр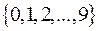 
.
Рассмотрим множество В, состоящее из двух элементов 0 и 1. Кортежи длины m из этих элементов обозначим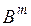 
. Тогда 
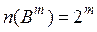. Такие кортежи называют векторами. Они имеют широкое применение в дискретной математике и не только.
Кортежи из 0 и 1 могут быть сообщениями, передаваемыми по некоторому каналу связи с помощью импульсов, каждый из которых принимает одно из двух значений, например азбука Морзе. Практический прикладной характер кортежей проявляется при использовании штриховых кодов, которые широко применяются для сообщении информации о характеристики объекта. Например, штрих-кодом снабжены все товары в магазине.
Декартовы произведения.
Декартовым произведением множеств X и Y называется множество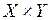 
всех упорядоченных пар (x, y) таких, что x 
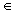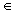X, y Y.
Пример. Найти декартово произведение множеств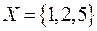 
и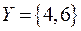 
.
Решение. Декартово произведение равно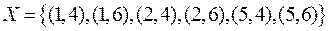 
.
Декартово произведение множества на себя называется декартовым квадратом и обозначается 
.