Возможность снижения вычислительных затрат при расчете больших схем вытекает из того, что в уравнении (3.70) большинство элементов равно нулю. Здесь матрица A эквивалентна одной из матриц схемы (матрице узловых проводимостей Y, контурных сопротивлений Z или др.), в зависимости от используемого в алгоритме метода составления уравнений схемы. Оценим коэффициент заполнения КЗ на примере матрицы узловых проводимостей Y. Подсчитано, что количество ненулевых элементов в в любой i -й строке матрицы Y лежит в пределах 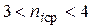 , в то время как полное количество элементов в строке равно числу узлов в схеме без одного (заземленного), т.е.
, в то время как полное количество элементов в строке равно числу узлов в схеме без одного (заземленного), т.е. 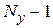 . Таким образом, среднее значение коэффициента заполнения может быть найдено, как
. Таким образом, среднее значение коэффициента заполнения может быть найдено, как 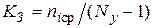 . Отсюда нетрудно рассчитать КЗ для схем различной сложности. Так для схем с числом узлов
. Отсюда нетрудно рассчитать КЗ для схем различной сложности. Так для схем с числом узлов 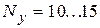 (низкий уровень интеграции)
(низкий уровень интеграции) 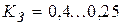 , для схем с числом узлов
, для схем с числом узлов 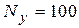 (средний уровень интеграции)
(средний уровень интеграции) 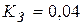 , с числом узлов
, с числом узлов 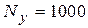 (БИС)
(БИС) 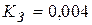 . Отсюда вытекает возможность значительной экономии памяти путем записи матрицы Y не в виде двумерного массива, занимающего
. Отсюда вытекает возможность значительной экономии памяти путем записи матрицы Y не в виде двумерного массива, занимающего 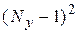 ячеек, а в виде одномерных массивов, записанных в определенном порядке.
ячеек, а в виде одномерных массивов, записанных в определенном порядке.
Хранение разреженной матрицы в памяти ЭВМ должно обеспечивать: 1) экономию памяти и числа операций, необходимых для преобразования матрицы в процессе решения системы линейных уравнений; 2) простоту доступа к любому элементу матрицы при формировании системы; 3)учитывать возможность появления новых ненулевых элементов в матрице.
Преобразование разреженной матрицы к верхней треугольной в процессе решения системы уравнений по методу Гаусса, в общем случае ведет к появлению новых ненулевых элементов. Поэтому при хранении разреженной матрицы места для этих элементов должны быть либо зарезервированы заранее, либо схема хранения должна позволять легко вводить новые элементы. Определение позиций новых элементов производится с помощью предварительного моделирования процесса вычислений, которое производится только один раз перед началом работы основной программы, так как структура разреженности не изменяется при анализе схемы.
Разработано несколько способов хранения разреженных матриц, обеспечивающих компромисс между противоречивыми требованиями экономии памяти и времени вычислений. Выбор того или иного способа зависит от специфики задачи и особенностей ЭВМ, на которой она решается.
В программах автоматизированного схемотехнического проектирования для решения линейных уравнений с разреженными матрицами используют некоторые из рассмотренных нами методов, из них наиболее употребительными остаются модификации схемы Гаусса, в особенности алгоритм Краута для LU-разложения матрицы.
Специфика этих методов применительно к операциям с разреженными матрицами состоит в том, что в процессе исключения неизвестных (прямого хода) происходит их заполнение ненулевыми элементами. Например, в схемах единственного деления на k -м шаге исключения вместо нулевого элемента 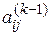 появляется ненулевой, если в преобразовании
появляется ненулевой, если в преобразовании
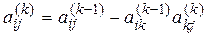
произведение 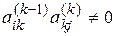 .
.
Обычно после прямого хода преобразованная матрица оказывается почти полностью заполненной. В связи с этим большое значение приобретает последовательность исключения неизвестных, от которой зависит количество новых ненулевых элементов. Правила выбора порядка исключения неизвестных, обеспечивающие минимальное число новых нулевых элементов, получили название критерия оптимальной нумерации. Из большого количества предложенных в литературе критериев, можно отметить критерий Марковица, в соответствии с которым для очередного исключения выбирается та неизвестная, координаты которой (i,j) удовлетворяют условию:
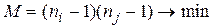 ,
,
где 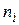 и
и 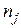 – число ненулевых элементов в строке i и столбце j.
– число ненулевых элементов в строке i и столбце j.
Величина M равна максимальному числу новых ненулевых элементов, которые могут появиться в результате исключения неизвестного с координатами (i,j). Более эффективный критерий предложили Сато и Тинней применительно к методу LU-разложения. Он основан на том, что количество ненулевых элементов в пересчитанной оставшейся части матрицы на каждом шаге LU-разложения зависит от того, какая пара столбец-строка была выбрана на предыдущем шаге разложения. Очевидно, что нужно выбирать те пары, при разложении по которым образуется минимальное количество новых ненулевых элементов. Из формулы (3.22)
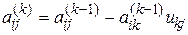
видно, что на месте нулевого элемента 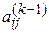 появится ненулевой элемент
появится ненулевой элемент 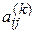 в том случае, если одновременно
в том случае, если одновременно 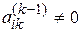 и
и 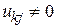 . Отсюда следует, что для минимизации числа новых ненулевых элементов на каждом шаге для разложения нужно выбирать ту пару столбец-строка, в которой минимальное число ненулевых произведений
. Отсюда следует, что для минимизации числа новых ненулевых элементов на каждом шаге для разложения нужно выбирать ту пару столбец-строка, в которой минимальное число ненулевых произведений 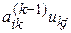 . Выбрав по этому правилу последовательность рассмотрения пар столбец-строка, нужно пронумеровать узлы схемы с этой последовательностью и сформировать матрицу A для новых номеров. Следует отметить, что нередко после очередного шага разложения возникает ситуация неопределенности, когда несколько пар столбец-строка дают одинаковое число новых ненулевых элементов. В этом случае выбирается та пара, в которой общее число ненулевых элементов максимально, так как при этом из дальнейшего рассмотрения исключается максимальное число ненулевых элементов.
. Выбрав по этому правилу последовательность рассмотрения пар столбец-строка, нужно пронумеровать узлы схемы с этой последовательностью и сформировать матрицу A для новых номеров. Следует отметить, что нередко после очередного шага разложения возникает ситуация неопределенности, когда несколько пар столбец-строка дают одинаковое число новых ненулевых элементов. В этом случае выбирается та пара, в которой общее число ненулевых элементов максимально, так как при этом из дальнейшего рассмотрения исключается максимальное число ненулевых элементов.
В целом методы оптимальной нумерации позволяют значительно снизить затраты памяти и времени на расчет схем с разреженными матрицами. Например, при расчете 100-узловой схемы применение оптимальной нумерации узлов ускоряет расчет почти в 40 раз. Принято считать, что затраты времени на решение системы линейных алгебраических уравнений определяются количеством длинных операций – умножения и деления, которое не может быть меньше 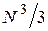 , где N – порядок системы. Затраты памяти при этом пропорциональны
, где N – порядок системы. Затраты памяти при этом пропорциональны 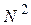 . Опыт свидетельствует, что при использовании алгоритма оптимальной нумерации затраты памяти и времени почти пропорциональны N.
. Опыт свидетельствует, что при использовании алгоритма оптимальной нумерации затраты памяти и времени почти пропорциональны N.
Метод подсхем.
Большая схема разбивается на несколько многополюсных подсхем 1-го уровня, те в свою очередь на подсхемы 2-го уровня и т.д. (по мере необходимости). В результате оказывается, что вся схема и каждая подсхема состоят из небольшого числа элементов в виде многополюсников. Составляются уравнения связывающие граничные и внутренние переменные для каждого многополюсника. Анализ такой составной схемы выполняется сверху вниз. Сначала решается уравнение, составленное относительно граничных переменных схемы последней ступени, затем находятся граничные переменные подсхем предыдущей ступени и т.д. В конце концов, определяются граничные переменные подсхем первой ступени, а по уравнениям связи – все внутренние переменные. После этого расчет линейной схемы заканчивается.
Эффективность этого метода практически н поступается эффективности метода разреженных матриц.
4 АНАЛИЗ НЕЛИНЕЙНЫХ РЕЗИСТИВНЫХ СХЕМ
на постоянном токе
До сих пор мы с вами рассматривали методы анализа линейных схем. Однако большинство радиотехнических устройств имеют в своем составе известные вам компоненты с нелинейной зависимостью тока от напряжения. Поэтому методы анализа линейных схем к ним в общем случае непригодны. Правда, в некоторых частных случаях, например, при работе устройства в режиме малых сигналов, нелинейные компоненты можно заменить их линейными моделями и тогда уже применять для анализа методы линейных схем. Однако и в этом случае параметры линеаризованной модели компонентов будут зависеть от режима их работы по постоянному току, т.е. от положения «рабочей точки» на их нелинейной характеристике. На постоянном токе схема становится чисто резистивной, поскольку все индуктивности становятся резисторами с нулевым сопротивлением, а емкости – резисторами с нулевой проводимостью.
4.1 Формирование узловых уравнений нелинейных схем
Рассмотрим достаточно типичный случай резистивной схемы, состоящей из линейных сопротивлений, нелинейных сопротивлений, управляемых напряжением, нелинейных источников тока, управляемых напряжением (ИТУН) и независимых источников. Это позволит нам обобщить ранее рассмотренный (см. раздел 2.1) алгоритм формирования узлового уравнения схемы на случай нелинейных цепей.
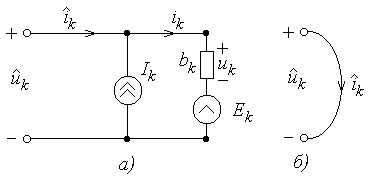 Рисунок 4.1
Рисунок 4.1
|
На рис.4.1 показана обобщенная ветвь и ее граф. Будем считать, что элемент 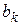 есть либо управляемая напряжением нелинейная проводимость
есть либо управляемая напряжением нелинейная проводимость
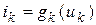 , (4.1)
, (4.1)
либо ИТУН с характеристикой
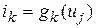 , (4.2)
, (4.2)
где 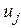 – напряжение на управляющем элементе
– напряжение на управляющем элементе 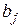 .
.
Заметим, что элемент 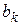 не может быть короткозамкнутой цепью, так как по условию он управляется напряжением. Уравнения (4.1) и (4.2) могут быть записаны в следующей компактной форме:
не может быть короткозамкнутой цепью, так как по условию он управляется напряжением. Уравнения (4.1) и (4.2) могут быть записаны в следующей компактной форме:
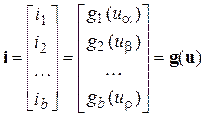 , (4.3)
, (4.3)
где 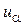 ,
,  ,...,
,..., 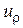 могут быть напряжениями любых ветвей
могут быть напряжениями любых ветвей 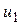 ,
, 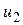 ,...,
,..., 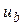 . Конечно, если нет управляемых источников, то
. Конечно, если нет управляемых источников, то 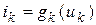 ,
, 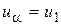 ,
, 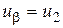 ,...,
,...,  .
.
Напомним, что закон токов Кирхгофа для узлов связной схемы может быть записан в матричном виде (3.2):
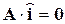 ,
,
где A – редуцированная матрица соединений (инциденций), 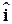 – вектор напряжений ветвей.
– вектор напряжений ветвей.
В свою очередь токи 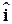 и напряжения
и напряжения 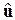 ветвей связаны с токами i и напряжениями u на элементах следующими соотношениями (3.15-3.16):
ветвей связаны с токами i и напряжениями u на элементах следующими соотношениями (3.15-3.16):
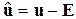 ,
,
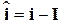 ,
,
где E и I – векторы напряжений и токов независимых источников.
Подставим выражение (4.3) в (3.16) и затем результат подставим в (3.2), откуда получим
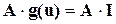 . (4.4)
. (4.4)
Теперь преобразование узлов (3.13):
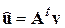 ,
,
подставим в (3.15) и преобразуем его к виду:
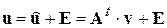 . (4.5)
. (4.5)
Наконец, подставив напряжения на элементах (4.5) в (3.2), окончательно получим:
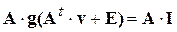 . (4.6)
. (4.6)
Для схемы с N +1 узлами уравнение (4.6) является системой из N нелинейных уравнений относительно N узловых напряжений. Если обозначить вектор 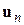 через x, то уравнение (4.6) может быть записано в следующей форме:
через x, то уравнение (4.6) может быть записано в следующей форме:
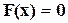 , (4.7)
, (4.7)
где
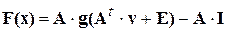 . (4.8)
. (4.8)
.
Уравнение (4.8) является системой нелинейных алгебраических уравнений (СНАУ), записанных в неявной форме. За исключением специальных случаев решения таких уравнений не могут быть получены в явной аналитической форме. Поэтому узловые уравнения обычно решаются с помощью приближенных численных методов.
Для решения системы (4.7) обычно пользуются итерационными методами, которые состоят в том, что на каждой итерации по известному n -му приближению корня 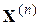 вычисляется (n+1)-е его приближение, которое лежит ближе к искомому значению точного корня
вычисляется (n+1)-е его приближение, которое лежит ближе к искомому значению точного корня 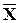 . Итерационный процесс считается законченным, когда норма вектора
. Итерационный процесс считается законченным, когда норма вектора 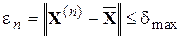 , где
, где 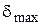 – заданная погрешность вычисления. В вычислительной математике разработано большое число итерационных методов численного решения систем нелинейных алгебраических уравнений. Наиболее распространенными в схемотехническом проектировании являются метод простой итерации и модификации метода Ньютона.
– заданная погрешность вычисления. В вычислительной математике разработано большое число итерационных методов численного решения систем нелинейных алгебраических уравнений. Наиболее распространенными в схемотехническом проектировании являются метод простой итерации и модификации метода Ньютона.
4.2 Метод простой итерации для решения систем нелинейных алгебраических уравнений
В методе простой итерации исходная система уравнений (4.8) преобразуется к приведенной форме:
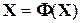 , (4.19)
, (4.19)
где 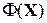 – итерирующая вектор-функция
– итерирующая вектор-функция
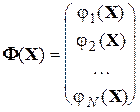 , (4.20)
, (4.20)
которую ищут в виде
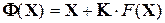 . (4.21)
. (4.21)
Подставляя (4.21) в (4.19) получаем итерационную формулу:
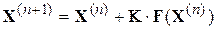 . (4.22)
. (4.22)
Обычно матрица K выбирается так
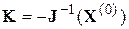 . (4.23)
. (4.23)
где 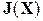 – матрица Якоби системы функций (
– матрица Якоби системы функций (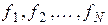 ) относительно переменных (x 1, x 2,..., xN):
) относительно переменных (x 1, x 2,..., xN):
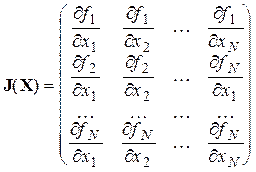 . (4.24)
. (4.24)
При этом предполагается, что матрица 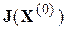 неособенная.
неособенная.
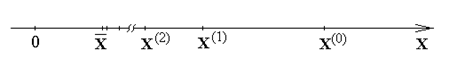
Рисунок 4.3 – Одномерная геометрическая интерпретация неподвижной точки
Если считать 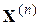 некоторой точкой на оси X (как это показано на рис.4.3), то алгоритм (4.22) можно интерпретировать как средство движения точки
некоторой точкой на оси X (как это показано на рис.4.3), то алгоритм (4.22) можно интерпретировать как средство движения точки 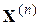 в следующую точку
в следующую точку 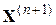 . Если расстояние между последовательными парами точек уменьшается достаточно быстро, то ясно, что алгоритм будет сходится к точке
. Если расстояние между последовательными парами точек уменьшается достаточно быстро, то ясно, что алгоритм будет сходится к точке 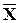 , относительно которой и происходят все эти последовательные движения. С точки зрения такой интерпретации точка
, относительно которой и происходят все эти последовательные движения. С точки зрения такой интерпретации точка 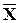 называется неподвижной точкой функции
называется неподвижной точкой функции 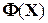 , а сам алгоритм иногда называют методом неподвижной точки.
, а сам алгоритм иногда называют методом неподвижной точки.
При соответствующих условиях последовательность 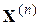 сходится к неподвижной точке:
сходится к неподвижной точке:
 . (4.25)
. (4.25)
Простой критерий, который гарантирует сходимость этого алгоритма, определяется следующей теоремой.
Принцип сжатых изображений. Если 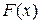 есть сжатие N -мерного пространства
есть сжатие N -мерного пространства 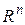 в
в 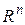 , т.е. имеется константа
, т.е. имеется константа 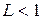 такая, что
такая, что
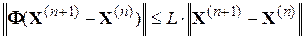 . (4.26)
. (4.26)
для всех 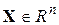 , то
, то 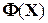 имеет единственную неподвижную точку
имеет единственную неподвижную точку 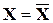 .
.
Рассмотрим подробно случай одного уравнения
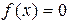 . (4.27)
. (4.27)
Его приведенная форма имеет вид
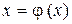 , (4.28)
, (4.28)
а итерационный процесс строится по схеме:
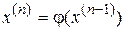 ,
, 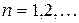 (4.29)
(4.29)
до выполнения условия 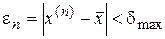 . При этом можно рекомендовать следующую формулу для верхней оценки погрешности n -го приближения:
. При этом можно рекомендовать следующую формулу для верхней оценки погрешности n -го приближения:
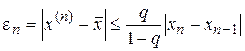 , (4.30)
, (4.30)
где 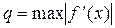 для
для 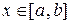 ,
, 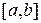 – отрезок, в котором находится корень уравнения.
– отрезок, в котором находится корень уравнения.
В качестве одного из способов приведения уравнения общего вида (4.27) к форме (4.28) можно рекомендовать такой, который основан на следующем выборе функции 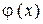 :
:
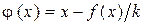 , (4.31)
, (4.31)
где k выбирается из условия 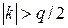 , а знак k совпадал бы со знаком
, а знак k совпадал бы со знаком 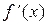 на отрезке
на отрезке 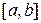 .
.
Процесс решения задачи легко поддается геометрической интерпретации. Введем в плоскости декартову систему координат 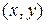 и построим в нем графики обеих частей уравнения – левой
и построим в нем графики обеих частей уравнения – левой 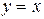 и правой
и правой 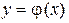 . Абсцисса точки пересечения этих двух линий и есть решение уравнения. Геометрически процесс приближений показан на рис.4.4.
. Абсцисса точки пересечения этих двух линий и есть решение уравнения. Геометрически процесс приближений показан на рис.4.4.
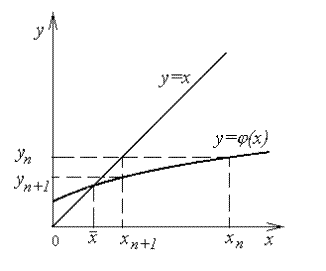
Рисунок 4.4
На (n +1)-м шаге, когда значение 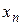 уже известно, вычисляется
уже известно, вычисляется 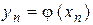 , т.е. восстанавливаем из
, т.е. восстанавливаем из 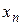 перпендикуляр до пересечения с линией
перпендикуляр до пересечения с линией 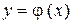 , затем из точки
, затем из точки 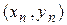 проводим горизонтальную прямую до пересечения с прямой
проводим горизонтальную прямую до пересечения с прямой 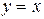 , при этом абсцисса новой точки пересечения есть (n +1)-е приближение корня, т.е.
, при этом абсцисса новой точки пересечения есть (n +1)-е приближение корня, т.е. 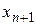 .
.
Для одного уравнения условие сходимости алгоритма обычно формулируется следующим образом. Итерационный процесс сходится, если функция 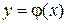 непрерывна на некотором отрезке
непрерывна на некотором отрезке 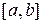 около
около 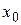
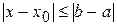
и удовлетворяет условию Липшица:
 ,
, 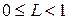 , (4.32)
, (4.32)
где x и 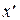 – любые две точки отрезка
– любые две точки отрезка 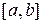 ,
, 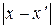 – расстояние между ними.
– расстояние между ними.
Наглядный смысл соотношения (4.32) весьма простой. Функция 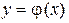 преобразует отрезок
преобразует отрезок 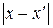 числовой оси в отрезок
числовой оси в отрезок 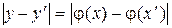 , который затем без преобразования превратится в новый отрезок
, который затем без преобразования превратится в новый отрезок 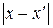 после операции присвоения
после операции присвоения 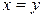 . Отношение
. Отношение 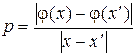 есть коэффициент изменения расстояния при преобразовании оператором j. Величина p ограничена числом L. Условие
есть коэффициент изменения расстояния при преобразовании оператором j. Величина p ограничена числом L. Условие  говорит о том, что при преобразовании происходит уменьшение отрезка
говорит о том, что при преобразовании происходит уменьшение отрезка 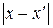 , следовательно операция
, следовательно операция 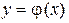 является сжатием. Если обозначить погрешность вычисления корня на n -м шаге итерации символом
является сжатием. Если обозначить погрешность вычисления корня на n -м шаге итерации символом 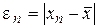 , то скорость сходимости можно определить приближенным соотношением:
, то скорость сходимости можно определить приближенным соотношением:
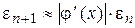 . (4.33)
. (4.33)
Отсюда следует, что метод простой итерации имеет линейную сходимость, а итерационный процесс на 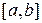 сходится при условии
сходится при условии 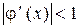 . Если
. Если 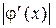 близок к единице, то итерационный процесс сходится очень медленно, а чем меньше
близок к единице, то итерационный процесс сходится очень медленно, а чем меньше 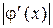 , тем сходимость его быстрее. Рассмотренный нами алгоритм, построенный по методу простой итерации, как и все другие алгоритмы с линейной сходимостью, принято относить к медленно сходящимся. Примером алгоритма с более высокой сходимостью может служить алгоритм, основанный на методе Ньютона.
, тем сходимость его быстрее. Рассмотренный нами алгоритм, построенный по методу простой итерации, как и все другие алгоритмы с линейной сходимостью, принято относить к медленно сходящимся. Примером алгоритма с более высокой сходимостью может служить алгоритм, основанный на методе Ньютона.
4.3 Метод Ньютона
Согласно методу Ньютона последовательные приближения для корней системы нелинейных уравнений находятся по формуле:
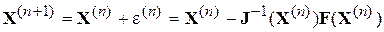 , (4.34)
, (4.34)
где 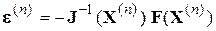 – поправки вектора,
– поправки вектора, 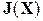 – матрица Якоби системы функций (
– матрица Якоби системы функций (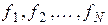 ) относительно переменных (x 1, x 2,..., x N).
) относительно переменных (x 1, x 2,..., x N).
За нулевое приближение 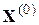 можно найти грубое приближение искомого корня.
можно найти грубое приближение искомого корня.
В случае одного уравнения с одним неизвестным матрица Якоби вырождается в обычную производную 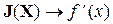 и выражение (4.34) преобразуется к виду:
и выражение (4.34) преобразуется к виду:
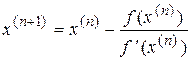 , (
, (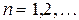 ). (4.35)
). (4.35)
Правило (4.35) имеет простой геометрический смысл. В плоскости с системой координат xOy построим график функции 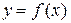 (рис.4.5).
(рис.4.5).
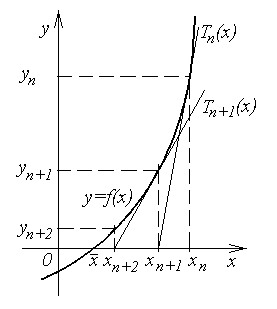
Рисунок 4.5
Точка пересечения 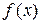 с осью
с осью 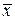 является решением уравнения (4.27). Отметим на оси Ox точку
является решением уравнения (4.27). Отметим на оси Ox точку 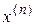 и рассмотрим на графике точку
и рассмотрим на графике точку 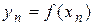 . В этой точке проведем к линии
. В этой точке проведем к линии 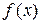 касательную
касательную 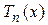 и найдем точку пересечения ее с осью Ox. Уравнение касательной есть
и найдем точку пересечения ее с осью Ox. Уравнение касательной есть 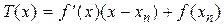 . Положив здесь левую часть равной нулю, можно определить точку
. Положив здесь левую часть равной нулю, можно определить точку 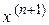 , в которой касательная пересекается с осью Ox. Нетрудно убедиться, что полученное таким образом значение
, в которой касательная пересекается с осью Ox. Нетрудно убедиться, что полученное таким образом значение 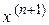 будет в точности совпадать с (4.35). Таким образом, правило Ньютона геометрически означает, что решение уравнения находится приближенно при помощи замены функции
будет в точности совпадать с (4.35). Таким образом, правило Ньютона геометрически означает, что решение уравнения находится приближенно при помощи замены функции 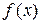 ее касательной
ее касательной 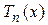 . Поэтому Метод Ньютона называют еще методом касательных.
. Поэтому Метод Ньютона называют еще методом касательных.
Можно показать, что метод Ньютона имеет квадратичную сходимость:
 , где
, где 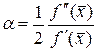 . (4.36)
. (4.36)
Из равенства (4.36) следует, что при 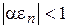 будет иметь место неравенство
будет иметь место неравенство 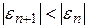 , т.е. последующее приближение будет ближе к искомому корню, чем предыдущее, а следовательно итерационный процесс сходится. Таким образом, при правильном выборе начального приближения метод Ньютона всегда сходится.
, т.е. последующее приближение будет ближе к искомому корню, чем предыдущее, а следовательно итерационный процесс сходится. Таким образом, при правильном выборе начального приближения метод Ньютона всегда сходится.
Ввиду квадратичной сходимости алгоритма итерационный процесс обычно идет до выполнения условия 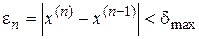 , где
, где 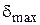 – заданная точность вычисления.
– заданная точность вычисления.
В литературе имеются исчерпывающиеся сведения о необходимых и достаточных условиях сходимости метода Ньютона, однако проблема выбора «удачного» начального приближения пока не решена. Несмотря на это, в силу целого ряда причин, в программах расчета электронных схем используется, как правило, метод Ньютона и его модификации.
4.4. Решение узловых уравнений методом Ньютона
Применим n -мерный метод Ньютона для решения нелинейного узлового уравнения:
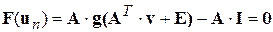 . (4.37)
. (4.37)
Матрица Якоби от  имеет вид:
имеет вид:
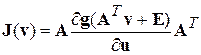 . (4.38)
. (4.38)
Следовательно, итерационный процесс Ньютона строится по такой формуле:
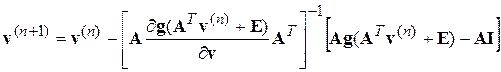 . (4.39)
. (4.39)
Установим физический смысл полученного уравнения, для чего перепишем его в следующем виде:
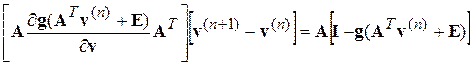 . (4.40)
. (4.40)
и сравним с узловым уравнением для линейной схемы
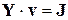 , (3.18)
, (3.18)
в котором
 ,
, 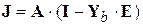 .
.
Уравнения (4.40) и (3.18) становятся очень похожими, если ввести следующие обозначения
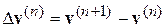 ; (4.41)
; (4.41)
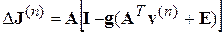 ; (4.42)
; (4.42)
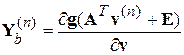 ; (4.43)
; (4.43)
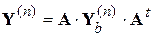 . (4.44)
. (4.44)
В таком случае (4.40) принимает вид:
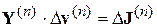 ,
,
где 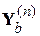 и
и 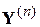 – матрицы дифференциальных проводимостей ветвей и узлов, а
– матрицы дифференциальных проводимостей ветвей и узлов, а 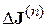 и
и 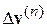 – приращение узловых источников токов и узловых напряжений на (n+1)-й итерации, которые показаны графически на рис.4.6 для k -й ветви.
– приращение узловых источников токов и узловых напряжений на (n+1)-й итерации, которые показаны графически на рис.4.6 для k -й ветви.
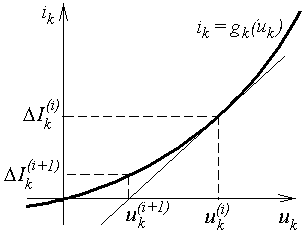
Рисунок 4.6
Отметим также, что в частном случае, когда все сопротивления линейны, 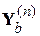 сводится к обычной матрице проводимостей ветвей
сводится к обычной матрице проводимостей ветвей 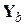 , и поэтому не зависит от номера итерации i.
, и поэтому не зависит от номера итерации i.
5 МОДЕЛИРОВАНИЕ электрических схем
ВО ВРЕМЕННОЙ ОБЛАСТИ
До сих пор мы рассматривали методы анализа резистивных схем на постоянном токе, т.е. в статическом режиме работы, и методы анализа линейных схем в частотной области, т.е. в стационарном (или установившемся) режиме работы. Сейчас мы переходим к рассмотрению динамического режима работы электрических схем во временной области, который еще называют переходным процессом. Мы будем рассматривать методы анализа линейных и нелинейных схем, когда входные сигналы являются функциями времени. Для простоты изложения основные выкладки мы будем делать для линейных схем, а затем результаты обобщим на нелинейный случай.
5.1. Математическая модель схемы для временной области.
Метод переменных состояния
В общем случае при составлении уравнений, описывающих колебания в электрических цепях, можно использовать методы напряжений (токов) ветвей, узловых напряжений или контурных токов. Для примера рассмотрим простую цепь, показанную на рис.5.1 и составим для нее уравнение для временной области, используя метод узловых напряжений.
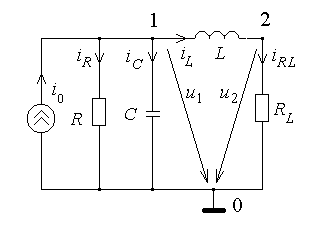
Рисунок 5.1
Записывая ЗТК для 1-го и 2-го узла, получаем систему интегро-дифференциальных уравнений следующего вида:
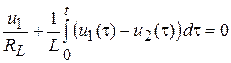 ;
;
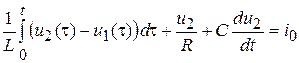
или в преобразованном виде:
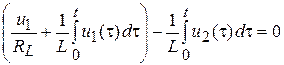 ;
;
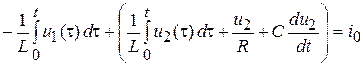 .
.
Решение интегро-дифференциальных уравнений есть достаточно сложная математическая задача, решение которой наталкивается на ряд вычислительных трудностей.
Значительно проще решать системы уравнений, которые не содержат интегральных слагаемых, а имеющие в своем составе только производные неизвестных функций, т.е. дифференциальные уравнения. Методы решения дифференциальных уравнений достаточно хорошо разработаны, в том числе и численные методы, ориентированные на применение ЭВМ. Поэтому в последние годы получил широкое распространение метод составления уравнений цепи, который приводит к модели схемы в виде системы обыкновенных дифференциальных уравнений. В этом методе, который получил название метода переменных состояния, неизвестными в системе уравнений являются так называемые переменные состояния, а именно напряжения на емкостях и токи в индуктивностях анализируемой электрической цепи. Эти переменные определяют как общий запас энергии в цепи, так и энергию, запасенную в каждом реактивном элементе цепи, т.е. определяют электромагнитное состояние цепи. Если значения этих неизвестных, т.е. переменных состояния, будут найдены, то после этого легко находятся токи и напряжения на зажимах любых других элементов цепи.
Действительно, если в некоторый момент времени найденное напряжение на p- й емкостной цепи равно 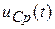 , то по теореме замещения этот элемент можно заместить источником напряжения с тем же задающим напряжением. Аналогично для того же момента времени q -ю индуктивность можно заменить источником тока с задающим током
, то по теореме замещения этот элемент можно заместить источником напряжения с тем же задающим напряжением. Аналогично для того же момента времени q -ю индуктивность можно заменить источником тока с задающим током 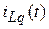 , значение которого известно. Если подобную замену выполнить для всех реактивных элементов цепи, то в результате образуется резистивная электрическая цепь, токи и напряжения в которой могут быть найдены методами анализа резистивных электрических цепей.
, значение которого известно. Если подобную замену выполнить для всех реактивных элементов цепи, то в результате образуется резистивная электрическая цепь, токи и напряжения в которой могут быть найдены методами анализа резистивных электрических цепей.
Для примера рассмотрим ту же цепь (рис.5.1), которую для удобства приведем к виду, показанному на рис.5.2, а. Если, например, найдены переменные состояния 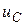 и
и 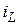 в этой цепи, то после указанной замены могут быть легко рассчитаны токи и напряжения в резистивной цепи, схема которой изображена на рис.5.2, б. Что касается определения самих переменных состояния, то они могут быть определены из уравнений, которые составляются на основе применения законов Кирхгофа.
в этой цепи, то после указанной замены могут быть легко рассчитаны токи и напряжения в резистивной цепи, схема которой изображена на рис.5.2, б. Что касается определения самих переменных состояния, то они могут быть определены из уравнений, которые составляются на основе применения законов Кирхгофа.
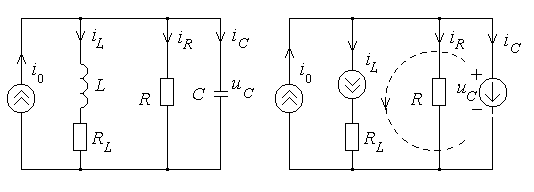
а) б)
Рисунок 5.2
Действительно, в соответствии с 1-м законом Кирхгофа
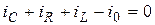 ,
,
поэтому
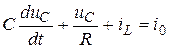 .
.
В соответствие же со 2-м законом Кирхгофа
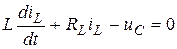 .
.
Эти уравнения образуют систему уравнений переменных состояния рассматриваемой цепи. Они содержат два дифференциальных уравнения относительно двух неизвестных. Преобразуем систему уравнений, выделив производные от переменных состояния в левые части уравнений, т.е. приведем ее к виду:
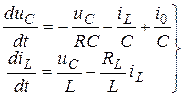 . (5.1)
. (5.1)
Такая форма представления дифференциальных уравнений называется канонической или нормальной. Если в произвольной линейной схеме, состоящей из  емкостей и
емкостей и 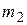 индуктивностей, обозначить переменные состояния
индуктивностей, обозначить переменные состояния 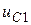 ,
, 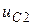 ,...,
,..., 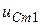 ,
, 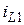 ,
, 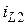 ,...,
,..., 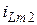 соответственно через
соответственно через 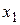 ,
, 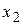 ,...,
,..., 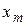 (
(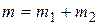 ), то система уравнений может быть записана в следующем общем виде:
), то система уравнений может быть записана в следующем общем виде:
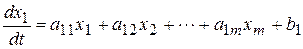 ;
;
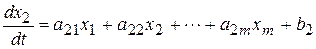 ; (5.2)
; (5.2)
................................
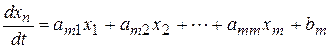

.
В этой системе коэффициенты 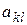 представляют собой вещественные числа, полученные в результате арифметических действий с параметрами элементов цепи, а функции
представляют собой вещественные числа, полученные в результате арифметических действий с параметрами элементов цепи, а функции 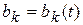 характеризуют заданные воздействия на электрическую цепь. Если хотя бы одна из этих функций не равна нулю, то соответствующая система уравнений будет неоднородной системой уравнений. В системе (5.1) функции
характеризуют заданные воздействия на электрическую цепь. Если хотя бы одна из этих функций не равна нулю, то соответствующая система уравнений будет неоднородной системой уравнений. В системе (5.1) функции 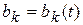 заданы соотношениями:
заданы соотношениями:
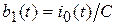 ,
, 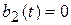 .
.
Матричная форма записи уравнений (5.2) имеет вид:
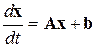 , или
, или 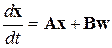 , (5.3)
, (5.3)
где 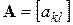 – матрица параметров цепи;
– матрица параметров цепи; 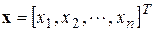 – матрица-столбец переменных состояния;
– матрица-столбец переменных состояния; 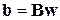 ; B – квадратная матрица;
; B – квадратная матрица; 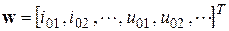 – матрица-столбец воздействий в виде токов и напряжений независимых источников.
– матрица-столбец воздействий в виде токов и напряжений независимых источников.
Для рассматриваемого примера:
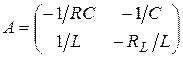 ;
;  ;
; 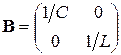 ;
; 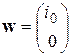 . (5.4)
. (5.4)
Таким образом, выбор переменных состояниям в виде токов в индуктивностях и напряжений на емкостях цепи в качестве неизвестных, подлежащих определению, приводит к тому, что:
а) математическая модель линейной схемы представляется системой обыкновенных дифференциальных уравнений первого порядка с постоянными коэффициентами;
б) сами переменные состояния характеризуют энергию, запасенную в реактивных элементах анализируемой цепи.
5.2. Решение уравнений переменных состояния линейных цепей
во временной области
Выше было показано, что для линейной схемы уравнение переменных состояния можно записать как:
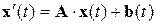 с начальным условием
с начальным условием 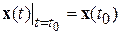 ,
,
или в более общем виде:
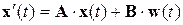 , (5.16)
, (5.16)
где 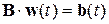 ,
,  – матрица-столбец неизвестных (переменных состояния),
– матрица-столбец неизвестных (переменных состояния), 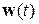 – столбец воздействий, A и B – квадратные матрицы.
– столбец воздействий, A и B – квадратные матрицы.
Определив из данного уравнения переменные состояния нетрудно потом найти все остальные переменные, описывающие режим работы схемы. В общем случае, эти переменные определяются следующим равенством:
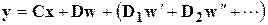 . (5.17)
. (5.17)
Если 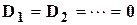 , то говорят, что линейная система является правильной, т.е. для нее
, то говорят, что линейная система является правильной, т.е. для нее
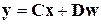 .
.
Решение уравнения (5.3) будем искать в виде:
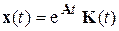 . (5.18)
. (5.18)
Неизвестной здесь является функция 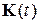 . Найдем ее, для чего подставим (5.18) в уравнение (5.3):
. Найдем ее, для чего подставим (5.18) в уравнение (5.3):
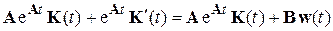 ,
,
откуда следует:
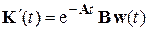 . (5.19)
. (5.19)
Интегрируем последнее равенство от 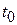 до t:
до t:
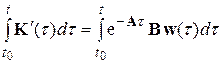 (5.20)
(5.20)
получаем:
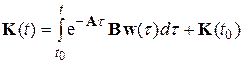 . (5.21)
. (5.21)
Из уравнений (5.18) и (5.21) имеем
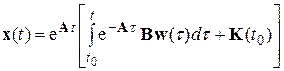 , (5.22)
, (5.22)
Найдем 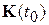 . Устремляя
. Устремляя 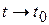 в (5.22), и
в (5.22), и