Теор. 1.2.2. Справедливы следующие равенства:
5. 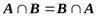 (коммутативность);
(коммутативность);
6. (А 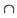 В)
В) 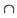 С=А
С=А 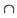 (В
(В  С) (ассоциативность);
С) (ассоциативность);
7. Если 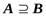 , то А
, то А  В = В;
В = В;
8. А  Ø=Ø.
Ø=Ø.
Разность двух множеств, дополнение до универсального. Свойства разности и дополнения.
1) Если заданы два множества, то можно не только найти их пересечение и объединение, но и вычесть из одного множества другое. Результат вычитания называют разностью и определяют следующим образом.
Определение. Разностью множеств А и В называют множество, содержащее все элементы, которые принадлежат множеству А и не принадлежат множеству В.
Разность множеств А и В обозначают А \ В. По определению: А \ В ={х/х∈А и х∉В}.
Определение: Пусть В⊂ А. Дополнением множества В до множества А называется множество, содержащее все элементы множества А, которые не принадлежат множеству В.
По определению: В´А ={х/х∈А и х∉В}.
Вычитание – это третья операция над множествами. Условились считать, что пересечение – более «сильная» операция, чем вычитание. Что касается вычитания и объединения, то их считают равноправными.
Вычитание множеств обладает рядом свойств. В частности можно доказать, что для любых множеств А, В и С справедливы следующие равенства:
1) (А \ В) \ С = (А \ С) \ В);
2) (А∪ В) \ С = (А \ С)∪ (В \ С);

Свойства разности множеств:
1. Если 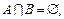 то А \ В = А.
то А \ В = А.
2. Если А Ì В, то А \ В = Æ.
3. А \ В = А \ (А 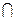 В).
В).
Разность между универсальным множеством U и множеством A называется дополнением множества A. Обозначение 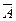 :
: 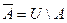 .
.
Свойства разности и дополнения:
1. 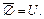 2. 2. 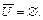 3. 3. 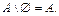 4. 4. 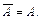 5. 5. 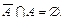 6. 6. 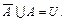 7. 7. 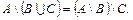
| 8. 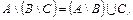 если если 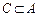 . 9. . 9. 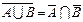 . 10. . 10. 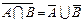 . 11. . 11. 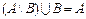 , если , если 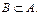 12. 12. 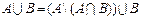 . .
|
Декартово произведение множеств. Изображение декартова произведения множеств на координатной плоскости. Свойства декартова произведения множеств.
1)Определение. Декартовым произведением множеств А и В называется множество всех пар, первая компонента которых принадлежит множеству А, а вторая компонента принадлежит множеству В.
Декартово произведение множеств А и В обозначают А х В. Используя это обозначение, записывают:А х В = {х; у) / х ∈ А и у∈В}. 
3) 1. Если 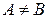 , то
, то 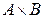
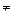
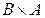 . То есть декартово произведение множеств не обладает свойством коммутативности.
. То есть декартово произведение множеств не обладает свойством коммутативности.
2. Декартово произведение множеств не обладает свойством ассоциативности: 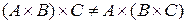 для любых множеств
для любых множеств 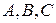 .
.
3. Если хотя бы одно из множеств А или В пусто, то и декартово произведение этих множеств есть множество пустое:
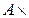 Ø= Ø
Ø= Ø 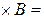 Ø
Ø 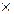 Ø = Ø.
Ø = Ø.
Это свойство следует из понятия декартова произведения и понятия пустого множества.
4. Для любых трех множеств 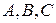 справедливы следующие утверждения:
справедливы следующие утверждения:
4.1. 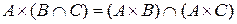
4.2. 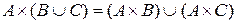
4.3. 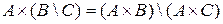
Вопрос.
Понятие множества и операций над множествами позволяют уточнить наше представление о классификации-действии распределения объектов по классам.
Определение. Считают, что множество Х разбито на классы Х1, Х2,…,Хп, если:
1. подмножества Х1, Х2,…,Хп попарно не пересекаются;
2. объединение подмножеств Х1, Х2,…,Хп совпадает с множеством Х.
Если не выполнено хотя бы одно из этих условий, классификацию считают не правильной.
Так, множество Х треугольников можно разбить на три класса: остроугольные, прямоугольные и тупоугольные. Действительно, выделенные подмножества попарно не пересекаются (среди остроугольных нет прямоугольных и тупоугольных, среди прямоугольных – тупоугольных) и их объединение совпадает с множеством Х.
Однако не всякая система подмножеств данного множества представляет собой разбиение этого множества. Например, если из множества Х треугольников выделить подмножества равнобедренных, равносторонних и разносторонний, то разбиения множества Х на классы не мы не получим, поскольку множества равнобедренных и равносторонних треугольников пересекаются (все равносторонние треугольники являются равнобедренными).
Итак, классификация связана с выделением из множества его подмножеств. Но чтобы выделить подмножество, достаточно указать характеристическое свойство его элементов.
Рассмотрим разбиение множества на классы, если для его элементов указать два свойства, т.е. выделить из множества два различных подмножества.
Рассмотрим два свойства натуральных чисел: «быть кратным 3» и «быть кратным 5».При помощи этих свойств из множества натуральных чисел можно выделить два подмножества: А- подмножество чисел, кратных 3, и В – подмножество чисел, кратных 5. Эти подмножества пересекаются, но ни одно из них не является подмножеством другого.
Проанализируем получившуюся картину. Круг, изображающий множество N натуральных чисел, разбился на 4 непересекающиеся области – они пронумерованы римскими цифрами. Каждая область изображает некоторое подмножество множества N. Определим, какие числа оказались в каждом из этих непересекающихся подмножеств. Подмножество I состоит из чисел, кратных 3 и 5; подмножество II – из чисел, кратных 3 и не кратным 5; подмножество III – из чисел, кратных 5 и не кратных 3; подмножество IY – из чисел, не кратных 3 и не кратных 5. Объединение этих четырех подмножеств есть множество N.
Не следует думать, что задание двух свойств элементов множества приводит к разбиению этого множества именно на 4 класса. Так бывает не всегда. Например, при помощи двух свойств «быть прямоугольным» и «быть тупоугольным» множество треугольников разбивается на три класса:
А - класс прямоугольных треугольников;
В - класс тупоугольных треугольников;
С - класс треугольников, не являющихся ни прямоугольными, ни тупоугольными треугольниками.
Вопрос

Вопрос.
Высказывание – это повествовательное предложение, о котором можно говорить, что оно истинно или ложно.
Процесс получения составных высказываний с помощью логических связок называется логической операцией.
По числу логических связок выделяют пять логических операций.
1. Негация (отрицание) – единственная операция, которая может применяться к одному высказыванию.
Негацией высказывания называется новое высказывание, которое истинно тогда и только тогда, когда само высказывание ложно и ложно, когда само высказывание истинно.
Негация обозначается, или b, читается: «не А» или «неверно, что А».
Например, высказывание А = «Луна – спутник Марса» – ложное, а высказывание = «Неверно, что Луна – спутник Марса» – истинное.
Для произвольного высказывания А определение удобно записывать с помощью так называемой таблицы истинности:
А
1 0
0 1
2. Конъюнкция (логическое умножение) – от латинского conjunctio – соединение.
Конъюнкцией двух высказываний называется новое высказывание, которое истинно тогда и только тогда, когда оба высказывания истинны.
Конъюнкция обозначается илиА&B; читается: «А и В».
Таблица истинности для конъюнкции выглядит следующим образом:
А В
1 1 1
1 0 0
0 1 0
0 0 0
Пример: Определить значение истинности высказываний «Париж расположен на Сене и 2 + 3 = 5»; «1 – простое число и 2 – простое число.
Решение. Первое высказывание является конъюнкцией двух высказываний А = «Париж расположен на Сене» и В = «2 + 3 = 5». Значение истинности высказывания А = 1 и значение истинности высказывания В = 1. Следовательно, = 1.
Второе высказывание является конъюнкцией высказываний А = «1 – простое число» (А = 0) и В = «2 – простое число» (В = 1). Следовательно, = 0.
3. Дизъюнкция (логическое сложение) – от латинского disjunction – разделение.
Дизъюнкцией двух высказываний является новое высказывание, которое ложно тогда и только тогда, когда оба высказывания ложны.
Дизъюнкция обозначается и читается «А или В».
Таблица истинности для дизъюнкции выглядит следующим образом:
А В
1 1 1
1 0 1
0 1 1
0 0 0
Пример: Определить значение истинности высказываний «1 – простое число или 2 – простое число»; «Число 3 – четное или медведи живут в Африке».
Решение.Второе высказывание является дизъюнкцией высказываний А = «1 – простое число» (А = 0) и В = «2 – простое число» (В = 1). Следовательно, = 1.
Третье высказывание является дизъюнкцией двух ложных высказываний, следовательно, =0.
4. Импликация (логическое следствие).
Импликацией двух высказываний называется новое высказывание, которое ложно тогда и только тогда, когда первое высказывание истинно, а второе – ложно.
Импликация обозначается или, читается «ЕслиА, то В» («Когда А, тогда В», «А, следовательно В»).
Таблица истинности импликации выглядит так:
А В
1 1 1
1 0 0
0 1 1
0 0 1
Компоненты импликации имеют свои собственные «имена»: предложение А называется посылкой или антецедентом, предложение В – заключением или консеквентом.
Пример: Чтобы запомнить правило нахождения значения истинности импликации, удобно воспользоваться следующими высказываниями: «Дождь идет», «Асфальт мокрый», «Дождь не идет», «Асфальт сухой».
1) = «Если дождь идет, то асфальт мокрый» = 1;
2) = «Если дождь идет, то асфальт сухой» = 0;
3) = «Если дождь не идет, то асфальт мокрый» = 1 (прошла поливальная машина или растаял снег);
4) = «Если дождь не идет, то асфальт сухой» = 1.
Принятое определение импликации соответствует употреблению союза «если…, то…» не только в математике, но и в обыденной, повседневной речи
5. Эквиваленция (логическая равносильность).
Эквиваленцией двух высказываний называется новое высказывание, которое истинно тогда и только тогда, когда оба высказывания одновременно истинны либо ложны.
Эквиваленция обозначается или, читается «А тогда и только тогда, когда В».
Таблица истинности для эквиваленции выглядит так:
А В
1 1 1
1 0 0
0 1 0
0 0 1
В форме эквиваленции, как правило, формулируются определения (например, определения логических операций).
Пример: Пусть через А обозначено высказывание «9 делится на 3», а через В – высказывание «10 делится на 3». Составьте высказывания, имеющие логическую структуру: а); б); в); г); д); е)и определите их значения истинности.
Решение. а) = «Если 9 делится на 3, то 10 делится на 3» = 0, т.к.А = 1, а В = 0. б) = «Если 10 делится на 3, то 9 делится на 3» = 1. в)= «9 делится на 3 тогда и только тогда, когда 10 делится на 3» = 0. г)= «10 делится на 3 тогда и только тогда, когда 9 делится на 3» = 0. д)= «Если 9 не делится на 3, то 10 делится на 3» = 1 (т.к.А = 1, то = 0 иВ = 0, следовательно, = 1). е)= «9 делится на 3 тогда и только тогда, когда 10 не делится на 3» = 1 (А = 1 и = 1, тогда= 1).
Свойства операций над высказываниями
1. а) (коммутативность дизъюнкции);
б) (коммутативность конъюнкции);
2. а) (ассоциативность дизъюнкции);
б) (ассоциативность конъюнкции);
3. а) (дистрибутивность дизъюнкции относительно конъюнкции);
б) (дистрибутивность конъюнкции относительно дизъюнкции);
4. и–законы де Моргана.
5.;;;
6. (или) (закон исключенного третьего);
(или (закон противоречия);
7. (или);(или);
(или);(или)
9.Высказывание с кванторами.Отрицание высказываний и предикатов
1.Высказывания с кванторами
В формулировках математических предложений часто встречаются слова: «каждый», «все», «некоторые», «хотя бы один». Например, свойство противоположных сторон прямоугольника формулируется так: «В любом прямоугольнике противоположные стороны равны», а о свойстве натуральных чисел мы говорили, что «некоторые натуральные числа кратны 3». Выясним, каков смысл этих слов и как они используются в математике.
Если задана высказывательная форма, то, чтобы превратить ее в высказывание, достаточно вместо каждой из переменных, входящих в форму, подставить ее значение. Например, если на множестве N натуральных чисел задана высказывательная форма А(х) – «число х кратно 5», то, подставив в нее вместо х число 20, мы получим истинное высказывание «число 20 кратно 5». Если же в эту высказывательную форму подставить вместо х число 17, мы получим ложное высказывание «число 17 кратно 5».
Однако существуют и другие способы получения высказываний из высказывательных форм.
Если перед высказывательной формой «число х кратно 5» поставить слово «всякое», то получится предложение «всякое число х кратно 5».Относительно этого предложения можно задать вопрос, истинно оно или ложно. Значит, оно является высказыванием, причем ложным.
Выражение «для всякого х» в логике называется квантором общности по переменной х (переменная может быть обозначена и другой буквой) и обозначается символом ∀х.
Запись (∀х.) А(х) означает: «для всякого значения х предложение А(х) – истинное высказывание.». Иногда эту запись дополняют обозначением множества Х, на котором задана высказывательная форма А(х), и тогда предложение можно читать:
а) для всякого х из множества Х истинно А(х);
б) всякий элемент из множества Х обладает свойством А.
Выражение «существует х такое, что…» в логике называется квантором существования по переменной х (переменная может быть обозначена и другой буквой) и обозначается символом ∃х.
Запись (∃х) А(х) означает: «существует такое значение х, что А(х) – истинное высказывание». Иногда эту запись дополняют обозначением множества Х, на котором задана высказывательная форма А(х), и тогда предложение (∃х) А(х) можно читать:
а) существует такое х из множества Х, что истинно А(х);
б) хотя бы один элемент х из множества Х обладает свойством А.
Заметим, что в математике наряду со словом «всякий» употребляют слова «каждый», «любой», а вместо слова «существует» используют слова «некоторые», «найдется», «есть», «хотя бы один».
Итак, если задана одноместная высказывательная форма А(х), то чтобы превратить ее в высказывание, достаточно связать квантором общности или существования содержащуюся в ней переменную. Если же высказывательная форма содержит несколько переменных, то перевести ее в высказывание можно, если связать квантором каждую переменную. Например, если дана высказывательная форма «х > у», то для получения высказывания надо связать квантором обе переменные: например, (∀х) (∃у) х > у или (∃х) (∃у) х > у.
Однако важно уметь не только переходить от высказывательной формы к высказыванию с помощью кванторов, но и распознавать их логическую структуру. Дело в том, что кванторы содержатся в формулировках определений, теорем и других математических предложений, хотя часто только подразумеваются. Например, в формулировке теоремы «Вертикальные углы равны» квантора в явном виде нет, но предполагается, что данное утверждение справедливо для всех вертикальных углов. Записывая коммутативное свойство сложения в виде а + b = b + а, подразумевают, что оно справедливо для любых чисел а и b.