КГБПОУ «Алтайский государственный колледж»
Реферат
По дисциплине техническая механика
Тема: «Геометрические характеристики плоских фигур»
Выполнил: Студент группа СМ 821
Тымыев Александр
Проверил: Преподаватель по технической механике
Лоскутова Е.Н
Барнаул 2018
Содержание
1. Понятие плоских фигур …………………………………………………………… 3
Геометрические характеристики прямоугольника и квадрата ….……………….3-4
Геометрические характеристики треугольника …………………………………. …4
Геометрические характеристики полукруга …..……………………………………. 4
2. Зависимости между моментами инерции относительно параллельных осей….5-9
2.1 Первый и второй частный случай
2.2 Примеры (4.2, 4.3, 4.4, 4.5)
Вывод …………………………………………………………………………….. 10
Источники..………………………………………………………………………. 11
Понятие плоских фигур
Плоская фигура — связное замкнутое подмножество R^2 {\displaystyle \mathbb {R} ^{2}}ZZz, ограниченное конечным числом попарно не пересекающихся жордановых кривых
Геометрические характеристики прямоугольника и квадрата
Осевые моменты инерции прямоугольника (квадрата)
Геометрические характеристики прямоугольного треугольника
Осевые моменты инерции прямоугольного треугольника
Геометрические характеристики равнобедренного треугольника
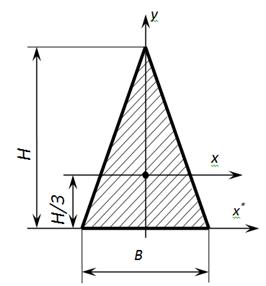
Осевые моменты инерции равнобедренного треугольника
Геометрические характеристики полукруга
Осевые моменты инерции полукруга
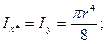
2. Зависимости между моментами инерции относительно параллельных осей
При вычислении моментов инерции для сложных фигур следует запомнить одно правило: значения для моментов инерции можно складывать, если они вычислены относительно одной и той же оси. Для сложных фигур чаще всего центры тяжести отдельных простых фигур и всей фигуры не совпадают. Не совпадают, соответственно, и центральные оси для отдельных простых фигур и всей фигуры. В связи с этим существуют приемы приведения моментов инерции к одной оси, например, центральной оси всей фигуры. Это может быть связано с параллельным переносом осей инерции и дополнительными вычислениями. Рассмотрим определение моментов инерции относительно параллельных осей инерции, изображенных на рис.4.9.
|
|
Рис.4.9
Пусть осевые и центробежный моменты инерции изображенной на рис.4.9. фигуры относительно произвольно выбранных осей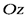 
и 
с началом координат в точке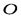 
известны.
Требуется вычислить осевые и центробежный моменты инерции фигуры относительно произвольных параллельных осей 
и 
с началом координат в точке 
. Оси и 
проведены на расстояниях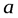 
и 
соответственно от осей 
и 
.
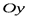Воспользуемся выражениями для осевых моментов инерции и для центробежного момента инерции. Подставим в эти выражения вместо текущих координат 
и 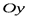элемента с бесконечно малой площадью координаты и 
в новой системе координат. Получим:
.
Анализируя полученные выражения, приходим к выводу, что при вычислении моментов инерции относительно параллельных осей к моментам инерции, вычисленных относительно исходных осей инерции, следует производить добавки в виде дополнительных членов, которые могут оказаться намного больше значений для моментов инерции относительно исходных осей. Поэтому пренебрегать этими дополнительными членами ни в коем случае нельзя.
|
|
Рассмотренный случай представляет собой самый общий случай параллельного переноса осей, когда в качестве исходных были взяты произвольные оси инерции.
В большинстве расчетов встречаются частные случаи определения моментов инерции.
Первый частный случай. Исходные оси являются центральными осями инерции фигуры. Тогда, используя основное свойство для статического момента площади, можно исключить из уравнений (4.18)-(4.20) члены уравнений, в которые входит статический момент площади фигуры. В результате получим:
. (4.21)
. (4.22)
. (4.23)
Здесь оси и -центральные оси инерции.
Второй частный случай. Исходные оси являются главными осями инерции. Тогда, учитывая, что относительно главных осей инерции центробежный момент инерции равен нулю, получим:
Здесь ос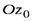и 
и 
-главные оси инерции.
Воспользуемся полученными выражениями и рассмотрим несколько примеров вычисления моментов инерции для плоских фигур.
Пример 4.2. Определить осевые моменты инерции фигуры, приведенной на рис. 4.10, относительно центральных осей 
и 
.
Рис.4.10
Решение:
В предыдущем примере 4.1 для изображенной на рис.4.10 фигуры было определено положение центра тяжести С. Координата центра тяжести откладывалась от оси 
и составила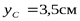 
. Вычислим расстояния 
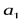и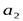 
между осями 
и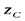 
и осями и . Эти расстояния составили соответственно 
и 
. Так как исходные ос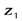и 
и 
являются центральными осями для простых фигур в виде прямоугольников, для определения момента инерции фигуры относительно оси 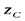воспользуемся выводами для первого частного случая, в частности, формулой (4.21).
|
|
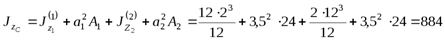см4.
Момент инерции относительно оси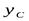 
получим путем сложения моментов инерции простых фигур относительно этой же оси, так как ось 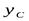является общей центральной осью для простых фигур и для всей фигуры.
см4.
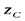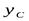Центробежный момент инерции относительно осей и равен нулю, так как ось инерции 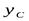является главной осью (осью симметрии фигуры).
Пример 4.3. Чему равен размер b (в см)фигуры, изображенной на рис. 4.11, если момент инерции фигуры относительно оси 
равен 1000 см4?
Рис.4.11
Решение:
Выразим момент инерции относительно оси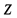 
через неизвестный размер сечения 
, воспользовавшись формулой (4.21), учитывая, что расстояние между осями 
и равно 7см:
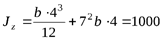см4. (а)
Решая выражение (а) относительно размера сечения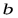 
, получим:
см.
Сравнивая полученные результаты, приходим к выводу, что наибольшим моментом инерции будет обладать сечение квадратной формы по сравнению с сечение круглой формы при одинаковой у них площади.
Пример 4.4. Определить полярный момент инерции (в см4) сечения прямоугольной формы относительно его центра тяжести, если ширина сечения 
см, высота сечения 
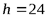см.
Решение:
1. Найдем моменты инерции сечения относительно горизонтальной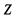 
и вертикальной 
центральных осей инерции:
см4; 
см4.
2. Определяем полярный момент инерции сечения как сумму осевых моментов инерции:
см4.
Пример 4.5. Определить момент инерции фигуры треугольной формы изображенной на рис.4.13, относительно центральной оси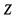 
, если момент инерции фигуры относительно оси равен 2400 см4.
Рис.4.13
Решение:
Момент инерции сечения треугольной формы относительно главной оси инерции будет меньше по сравнению с моментом инерции относительно оси на величину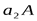 
. Поэтому при 
см момент инерции сечения относительно оси 
найдем следующим образом:
см4.
ВЫВОД:
Анализируя полученное решение, можно сделать вывод о том, что при определении центра тяжести для простых фигур очень важно удачно выбрать начало координат и оси, относительно которых производятся все вычисления. Как уже отмечалось выше, начало координат следует помещать в центр тяжести одной из простых фигур.
Источники
https://sopromato.ru/info/geometric-characteristics-of-figures
https://studfiles.net/preview/5397440/page:4/
https://yandex.ru/images/search?text=плоские%20фигуры%20тех%20мех
https://yandex.ru/images/search?text=Определение%20геометрический%20характеристик%20плоских%20фигур