Основан на связи между решениями прямой и двойственной задач.
Рассмотрим задачу ЛП, представленную в канонической форме:
 1)
1)
 2)
2)
 3)
3)
и задачу двойственную к ней
 4)
4)
 5)
5)
Пусть Y=(y1, y2, …, ym) – опорный план задачи 4), 5).
Базисом опорного плана задачи 4), 5) либо сопряженным базисом, называется произвольная система m линейно независимых векторов  условий задачи 1)-3), для которых не более m ограничений 5) выполняются как строгие равенства и найденное решение удовлетворяет всем неравенствам 5).
условий задачи 1)-3), для которых не более m ограничений 5) выполняются как строгие равенства и найденное решение удовлетворяет всем неравенствам 5).
Свяжем с каждым сопряженным базисом Бу =  m –мерный вектор Х=(х1, х2, …, хm), компоненты которого удовлетворяют условиям 2) исходной задачи.
m –мерный вектор Х=(х1, х2, …, хm), компоненты которого удовлетворяют условиям 2) исходной задачи.
Вектор Х=(х1, х2, …, хm), компоненты которого равны коэффициентам разложения вектора А0=(b1,b2, …,bm) по системе Бу =  называется псевдопланом задачи 1)-3).
называется псевдопланом задачи 1)-3).
Признак оптимальности. Если среди базисных компонентов псевдоплана Х=(х1, х2, …, хm) нет отрицательных, т.е. все  , то псевдоплан Х-решение задачи 1)-3).
, то псевдоплан Х-решение задачи 1)-3).
Свяжем с каждым сопряженным базисом Бу =  матрицу (Хij)
матрицу (Хij) 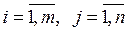 , элементы которой совпадают с коэффициентами разложения векторов условий Аj задачи 1)-3) по системе Бу.
, элементы которой совпадают с коэффициентами разложения векторов условий Аj задачи 1)-3) по системе Бу.
Пусть среди базисных компонентов псевдоплана Х=(х1, х2, …, хm) имеются отрицательные. Если среди компонентов хij<0 найдется хотя бы один, для которого все хij>0, то целевая функция задачи 4)-5) не ограничена снизу на множестве ее планов, а прямая задача 1)-3) не разрешима.
Если среди базисных компонентов Х найдется хотя бы один, для которого существует хij<0, то псевдоплан можно улучшать.
Для того, чтобы получить базис нового псевдоплана Хл, нужно вывести из базиса псевдоплана Х вектор Аr(xrj<0).
Если хi0<0 при нескольких значениях r, из базиса нужно вывести вектор с minхr0. Для определения вектора, который нужно ввести в базис, необходимо найти номер k, на котором достигается минимум отношения.

В базис вводится вектор Ак и определяются параметры следующей итерации по формуле:

F=8x1+6x2→max 6)
2х1+5х2≤11
4х1+х2≤10 7)
х1, х2≥0 8)
Приведем к каноническому виду
| А1 | А2 | А3 | А4 | А0 | |
| 2х1 | + 5х2 | + 1х3 | + 0х4 | = 11 | |
| 4х1 | + х2 | +0 х3 | + 1.х4 | = 10 | |

| |||||
Запишем двойственную к ней
F*=11у1+10у2→min
2y1+4y2≥8 A1
5y1+ y2 ≥6 A2
y1 ≥0 A3
y2 ≥0 A4
Возьмем в качестиве сопряженного базиса вектора А1, А3 и из системы
2у1 +4у2 = 8
у1 = 0 найдем значение опорного плана двойственной задачи
у1 =0, у2 =2
Данный базис не может быть взят в качестве сопряженного, т.к. второе ограничение не выполняется (2≥6).
Возьмем сопряженным базисом А2, А3. Из системы
5у1 + у2 = 6
у1 = 0 находим значения у1 =0, у2 =6.
Неравенство 2у1 +4у2 ≥ 8 при этих значениях у1 и у2 выполняется и, следовательно, система { А2, А3} является сопряженным базисом.
Определяем коэффициенты разложения небазисных векторов по векторам базиса и находим псевдопланы исходной задачи:
А0 = А2х20 +А3х30

х20= 10; х30= -39
А1 = А2х21 +А3х31

х21= 4; х31 = -18
А4 = А2х24 +А3х34
х24= 1; х34 = -5
| Аб | Сб | А0 | 8 | 6 | 0 | 0 |
| А1 | А2 | А3 | А4 | |||
| А2 | 6 | 10 | 4 | 1 | 0 | 1 |
| А3 | 0 | -39 | -18 | 0 | 1 | -5 |
| ∆ | 60 | 16 | 0 | 0 | 6 | |
| Θ | - | 16/18 | - | - | 6/5 |
| А2 | 6 | 4/3 | 0 | 1 | 2/9 | 1/9 | |
| А1 | 8 | 39/18 (13/6) | 1 | 0 | 
| 5/18 | (-4) |
| ∆ | 60 | 16 | 0 | 0 | 6 |
Двойственный симплекс-метод целесообразнее использовать при решении ЗЛП, в которой нужно вводить фиктивные переменные.
F=3x1+2x2+5x3→min
2x1-3x2+x3 ≥ 10
4x1+x2+2x3 ≥ 15
xj ≥ 0 (j=  ) )
| 
|  =-3x1-2x2-5x3→min
2x1-3x2+x3 –x4 = 10
4x1+x2+2x3 –x5= 15 =-3x1-2x2-5x3→min
2x1-3x2+x3 –x4 = 10
4x1+x2+2x3 –x5= 15
|
| Двойственная задача F*=10у1+15у2→min 2у1+4у2 ≥-3 А1 -3у1+ у2 ≥-2 А2 у1 +2у2 ≥-5 А3 -у1 ≥ 0 А4 -у2 ≥ 0 А5 |
{А4, А5} – сопряженный базис → у1=0; у2=0
Базисные компоненты псевдоплана Х совпадают с соответствующими составляющими вектора ограничений, взятыми с обратным знаком, а элементы хij столбцов Aj равны и противоположны по знаку элементам соответствующих столбцов матрицы условия.
| Аб | Сб | А0 | -3 | -2 | -5 | 0 | 0 |
| А1 | А2 | А3 | А4 | А5 | |||
| А4 | 0 | -10 | -2 | 3 | -1 | 1 | 0 |
| А5 | 0 | -15 | -4 | -1 | -2 | 0 | 1 |
| ∆ | 0 | 3 | 2 | 5 | 0 | 0 | |
| θ | 3/4 | 2 | 5/2 |
| А4 | 0 | -5/2 | 0 | 7/2 | 0 | 1 | -1/2 | |
| А1 | -3 | 15/4 | 1 | 1/4 | 1/2 | 0 | -1/4 | (2) |
| ∆ | -45/4 | 0 | 5/4 | 7/2 | 0 | 3/4 | ||
| θ |
| А5 | 0 | 5 | 0 | -7 | 0 | -2 | 1 | (1/4) |
| А1 | -3 | 5 | 1 | -3/2 | 1/2 | -1/2 | 0 | |
| -15 |
Fmin = 15, x1 = 5; x2= … = 0