Площадь боковой и полной поверхности конуса
Площадь боковой поверхности конуса
Мы знаем, что такое конус, попробуем найти площадь его поверхности. Зачем нужно решать такую задачу? Например, нужно понять, сколько теста пойдет на изготовление вафельного рожка? Или сколько кирпичей понадобится, чтобы сложить кирпичную крышу замка?
Измерить площадь боковой поверхности конуса просто так не получится. Но представим себе все тот же рожок, обмотанный тканью. Чтобы найти площадь куска ткани, нужно разрезать и разложить ее на столе. Получится плоская фигура, ее площадь мы сможем найти.
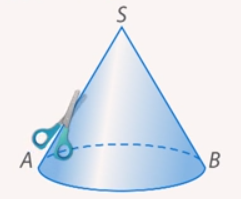
Рис. 1. Разрез конуса по образующей
Сделаем так же с конусом. «Разрежем» его боковую поверхность вдоль любой образующей, например, 
(см. рис. 1).
Теперь «размотаем» боковую поверхность на плоскость. Получаем сектор. Центр этого сектора – вершина конуса, радиус сектора равен образующей конуса, а длина его дуги совпадает с длиной окружности основания конуса. Такой сектор называется разверткой боковой поверхности конуса (см. рис. 2).
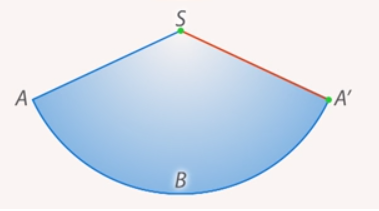
Рис. 2. Развертка боковой поверхности
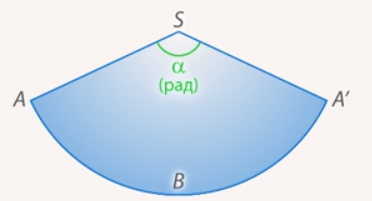
Рис. 3. Измерение угла в радианах
Попробуем найти площадь сектора по имеющимся данным. Сперва введем обозначение: пусть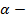 
угол при вершине сектора в радианах (см. рис. 3).
Угол при вершине развертки конуса
С углом при вершине развертки нам придется часто сталкиваться в задачах. Пока же попробуем ответить на вопрос: а не может ли этот угол получиться больше 360 градусов? То есть не получится ли так, что развертка наложится сама на себя? Конечно же, нет. Докажем это математически. Пусть развертка «наложилась» сама на себя. Это означает, что длина дуги развертки больше длины окружности радиуса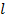 
. Но, как уже было сказано, длина дуги развертки есть длина окружности радиуса 
. А радиус основания конуса, разумеется, меньше образующей, например, потому, что катет прямоугольного треугольника меньше гипотенузы
Тогда вспомним две формулы из курса планиметрии: длина дуги 
. Площадь сектора: 
.
В нашем случае роль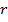 
играет образующая 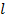, а длина дуги равна длине окружности основания конуса, то есть 
. Имеем: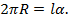 
Окончательно получаем: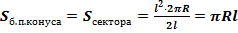 
.
Площадь полной поверхности конуса
Наряду с площадью боковой поверхности можно найти и площадь полной поверхности. Для этого к площади боковой поверхности надо прибавить площадь основания. Но основание – это круг радиуса , чья площадь по формуле равна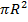 
.
Окончательно имеем: 
, где – радиус основания цилиндра, 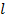– образующая.
Примеры задач на применение выведенных формул
Решим пару задач на приведенные формулы.
Рис. 4. Искомый угол
Пример 1. Разверткой боковой поверхности конуса является сектор с углом 
при вершине. Найти этот угол, если высота конуса равна 4 см, а радиус основания равен 3 см (см. рис. 4).
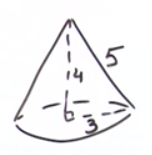
Рис. 5. Прямоугольный треугольник, образующий конус
Решение
Первым действием, по теореме Пифагора, найдем образующую: 5 см (см. рис. 5). Далее, мы знаем, что 
.
Ответ: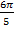 
.
Пример 2. Площадь осевого сечения конуса равна 
, высота равна 
. Найти площадь полной поверхности (см. рис. 6).
Рис. 6. Иллюстрации к задаче
Решение
; 
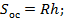
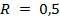
Тогда, по теореме Пифагора, 
.
Ответ: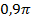 
.