УМК «Управление технологическими процессами атомных электростанций»
Типовые задачи с решениями и MATHCAD программами
Часть 1
Разработано в рамках мероприятия 2.5.5.1
Авторы Н.Н.Акифьева, Р.В.Радченко
(рекомендуется как учебное пособие при изучении дисциплины «Теория автоматического регулирования»
ООП бакалавриата направления 140400 «Ядерная энергетика и теплофизика»)
Пояснения к задачам 1-10.
Общее решение НЛДУ можно представить как сумму общего решения соответствующего однородного уравнения (ОЛДУ) -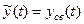 
и частного решения неоднородного уравнения (НЛДУ) - 
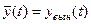. Индексы «св.» и «вын.» Здесь означают, что функция, представляющая общее решение ОЛДУ, описывает свободное «движение» системы, после нанесения возмущения (или передачи управления), а функция, представляющая частное решение НЛДУ, описывает вынужденное движение системы.
Общее решение однородного линейного дифференциального уравнения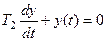 
может быть записано в виде:
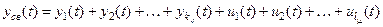, где
- функции решения, соответствующие действительным корням характеристического уравнения, а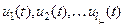 
- функции решения, соответствующие комплексно-сопряженным корням характеристического уравнения. Для того, что записать перечисленные функции в общем виде, рассмотрим виды корней характеристического уравнения.
ОЛДУ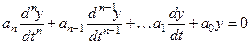 
ставится в соответствие алгебраическое характеристическое уравнение:
, полином левой части которого можно представить в виде (вид соответствует разложению по корням):
.
При этом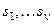 
- различные действительные корни кратности 
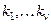, а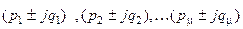 
- различные пары комплексно-сопряженных корней кратности 
, 
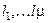, где 
- порядок дифференциального уравнения. Отдельным сомножителям полинома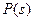 
, представляющим разложение по 
-му действительному корню поставим в соответствие следующие функции общего решения ОЛДУ:
Сомножителям полинома 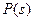, представляющим разложение по -й паре комплексно сопряженных корней поставим в соответствие следующие функции общего решения ОЛДУ:
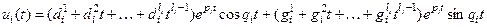
Количество всех коэффициентов – произвольных постоянных 
должно быть в точности равно порядку дифференциального уравнения 
Частное решение НЛДУ находится достаточно просто, если функция правой части имеет специальный вид. В теории автоматического регулирования рассматриваются так называемые характеристические случаи, когда на вход АСР или звена подается ступенчатое возмущение, импульсное возмущение или гармонический сигнал. Более сложные входные сигналы раскладываются на простые и, благодаря суперпозиции решения, имеющего место для линейных дифференциальных уравнений, переходные процессы при таких сложных возмущениях, могут быть представлены как сумма переходных процессов, являющихся реакциями на простые возмущения (на которые был разложен входной сигнал).
Если правая часть НЛДУ имеет вид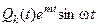 
или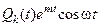 
, то частное решение ищется в виде 
, 
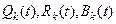-полиномы 
-й степени, если 
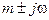не является корнем характеристического уравнения. Если 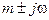является корнем характеристического уравнения, то частное решение ищется в виде 
, где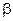 
- кратность корня 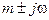. Если правая часть представляет собой линейную. Комбинацию вышеуказанных функций, то частное решение уравнения равно сумме решений, соответствующих каждому члену линейной комбинации.
Задача 1.
Решить неоднородное линейное дифференциальное уравнение (НЛДУ), описывающее простой переходный процесс устойчивой линейной АСР (вынужденное «движение»). Построить график переходного процесса, выделяя в возмущенном «движении» вынужденные и свободные составляющие.
Передаточная функция системы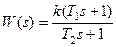 
(1).
Дифференциальное уравнение АСР, получаемое в результате обратного преобразования Лапласа для левой и правой части выражения (1)
:
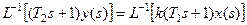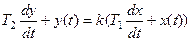(2)
Простой переходный процесс – это характеристический процесс линейной АСР или ее отдельного звена, исследуемый при подаче на вход АСР простого ступенчатого возмущения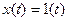 
. Подставим в правую часть выражения (2) :
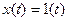(3). Полученное выражение – есть выражение неоднородного линейного дифференциального уравнения 1-го порядка с постоянными коэффициентами (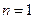
).
Общее решение этого уравнения можно представить как сумму общего решения соответствующего однородного уравнения (ОЛДУ) - 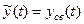и частного решения неоднородного уравнения (НЛДУ) - .
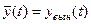Для нахождения общего решения ОЛДУ запишем характеристическое уравнение:
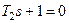. Это уравнение имеет один действительный корень - 
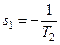. Зная корни характеристического уравнения, можно записать общее решение ОЛДУ:
.
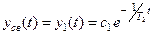Для нахождения частного решения представим функцию правой части в виде :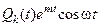
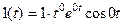, т.е. 
, 
, 
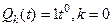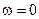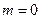. Комплексное число 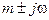, которое в нашем случае есть 
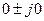не совпадает с единственным корнем характеристического уравнения. Следовательно, частное решение НЛДУ:
.
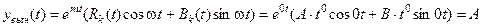Для определения значение постоянной А подставим полученное частное решение в дифференциальное уравнение (2):
, то есть 
.
Тогда общее решение НЛДУ, описывающее простой переходный процесс в АСР
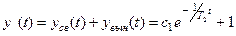. Значение коэффициента 
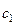должно быть найдено из начальных условий. Отметим, что в условии задачи не оговаривались начальные условия. Для решения НЛДУ, описывающего характеристический переходный процесс в линейной АСР, эти условия всегда нулевые по функции и всем актуальным для этого уравнения производным. Таков принцип анализа АСР в линейной теории автоматического регулирования, следующий из суперпозиции переходных процессов по отдельным возмущениям. Из нулевых начальных условий получаем
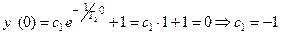
Таким образом, функция, описывающая простой переходный процесс в исследуемой АСР 
, при этом функция, описывающая свободное движение - 
, а функция, описывающая вынужденное движение -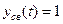 
.
Переходный процесс, характерный для АСР первого порядка, имеющей один действительный отрицательный корень характеристического уравнения, называется апериодическим, поскольку не имеет колебательной составляющей в свободном «движении».
Построим график простого переходного процесса в данной АСР, выделяя свободную и вынужденную составляющую, для чего воспользуемся программой MATHCAD.
На графиках представлены простые переходные процессы трех апериодических АСР, различающихся постоянными времени.
MATHCAD программа к задаче 1.
Задача 2.
Решить неоднородное линейное дифференциальное уравнение (НЛДУ), описывающее переходный процесс неустойчивой линейной АСР, имеющей положительные действительные корни характеристического уравнения (вынужденное «движение»). Построить график переходного процесса, выделяя в возмущенном «движении» вынужденные и свободные составляющие.
Передаточная функция системы 
(1).
Дифференциальное уравнение АСР, получаемое в результате обратного преобразования Лапласа для левой и правой части выражения (1)
:
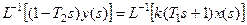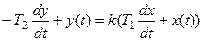(2)
Простой переходный процесс – это характеристический процесс линейной АСР или ее отдельного звена, исследуемый при подаче на вход АСР простого ступенчатого возмущения 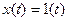. Подставим в правую часть выражения (2) :
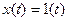(3).
Полученное выражение – есть выражение неоднородного линейного дифференциального уравнения 1-го порядка с постоянными коэффициентами ().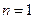
Общее решение этого уравнения можно представить как сумму общего решения соответствующего однородного уравнения (ОЛДУ) - 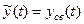и частного решения неоднородного уравнения (НЛДУ) - .
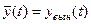Для нахождения общего решения ОЛДУ запишем характеристическое уравнение:
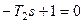. Это уравнение имеет один действительный корень - 
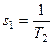. Зная корни характеристического уравнения, можно записать общее решение ОЛДУ:
.
Для нахождения частного решения представим функцию правой части в виде :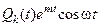
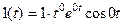, т.е. 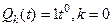, , 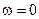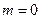. Комплексное число 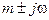, которое в нашем случае есть 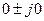не совпадает с единственным корнем характеристического уравнения. Следовательно, частное решение НЛДУ:
.
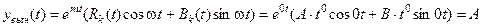Для определения значение постоянной А подставим полученное частное решение в дифференциальное уравнение (2):
, то есть .
Тогда общее решение НЛДУ, описывающее простой переходный процесс в АСР
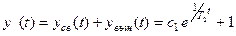. Значение коэффициента 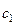должно быть найдено из начальных условий. Отметим, что в условии задачи не оговаривались начальные условия. Для решения НЛДУ, описывающего характеристический переходный процесс в линейной АСР, эти условия всегда нулевые по функции и всем актуальным для этого уравнения производным. Таков принцип анализа АСР в линейной теории автоматического регулирования, следующий из суперпозиции переходных процессов по отдельным возмущениям. Из нулевых начальных условий получаем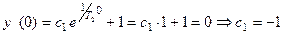 
Таким образом, функция, описывающая простой переходный процесс в исследуемой АСР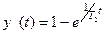 
, при этом функция, описывающая свободное движение - 
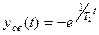, а функция, описывающая вынужденное движение - .
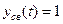Переходный процесс, характерный для АСР первого порядка, имеющей один действительный положительный корень характеристического уравнения не будет иметь конечного предела при времени, стремящемся к бесконечности, поскольку не будет конечного предела у функции, описывающей свободное движение. АСР, у которых после прекращения входного воздействия, выходная переменная самопроизвольно не переходит к новому установившемуся состоянию, называются неустойчивыми.
Построим график простого переходного процесса в данной АСР, выделяя свободную и вынужденную составляющую, для чего воспользуемся программой MATHCAD.
