Многоугольник распределения ДСВ – графическое изображение ряда распределения ДСВ в декартовой системе координат.

Многоугольник распределения для ДСВ 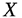 , принимающей значения
, принимающей значения 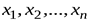 с вероятностями
с вероятностями 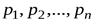 соответственно.
соответственно.
Аналитическая форма представление закона распределения ДСВ с помощью формулы
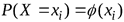
Функция распределения 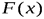 ДСВ
ДСВ 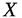 есть разрывная, ступенчатая функция, скачки которой соответствуют возможным значениям
есть разрывная, ступенчатая функция, скачки которой соответствуют возможным значениям 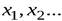 случайной величины
случайной величины 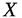 и равны вероятностям
и равны вероятностям 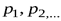 этих значений. Между скачками функция
этих значений. Между скачками функция 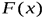 сохраняет постоянное значение. В точке разрыва функция
сохраняет постоянное значение. В точке разрыва функция 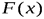 равна тому значению, с которым она подходит к точке разрыва слева, т.е.
равна тому значению, с которым она подходит к точке разрыва слева, т.е. 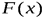 - непрерывна слева.
- непрерывна слева.

График функции распределения ДСВ 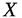 , принимающей значения
, принимающей значения 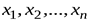 .
.
Многоугольником распределения вероятностей данной величины называют ломаную, звенья которой соединяют соседние точки 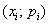 . Термин, на мой взгляд, не слишком удачен, но так сошлись звёзды.
. Термин, на мой взгляд, не слишком удачен, но так сошлись звёзды.
Всё очень просто:
Пример 11
Построить многоугольник распределения вероятностей случайной величины 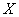

Решение: чертим прямоугольную систему координат, в которой по оси абсцисс отсчитываются 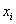 – значения случайной величины, а по оси ординат
– значения случайной величины, а по оси ординат 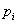 – их вероятности. Отмечаем на чертеже точки
– их вероятности. Отмечаем на чертеже точки 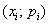 , в данном случае их пять, и соединяем «соседей» отрезками:
, в данном случае их пять, и соединяем «соседей» отрезками:
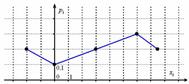
При выполнении чертежа от руки по возможности придерживайтесь следующего масштаба:
горизонтальная ось: 1 ед. = 2 тетрадные клетки (1 см);
вертикальная ось: 0,1 = 2 тетрадные клетки.
Если значения 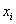 достаточно велики, то ось абсцисс можно «разорвать» (не чертить её кусочек после единицы), и справа продолжить нумерацию, например, с 20.
достаточно велики, то ось абсцисс можно «разорвать» (не чертить её кусочек после единицы), и справа продолжить нумерацию, например, с 20.
Теперь обратите внимание на следующую важную вещь: помимо того, что дискретную случайную величину можно изобразить с помощью многоугольника – её ведь можно ещё и ЗАДАТЬ этим способом. До сих пор мы делали это с помощью таблички, но никто же не мешает использовать и чертёж:
Пример 12
Дискретная случайная величина 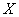 задана своим многоугольником
задана своим многоугольником
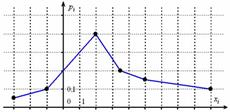
Записать закон распределения данной случайной величины.
Это задание для самостоятельного решения.
Иногда вместо «многоугольника» говорят о полигоне распределения вероятностей, но этот вариант больше применим в математической статистике.
На практике разобранные задачи встречаются не так уж редко, и поэтому я счёл нужным включить их в данную статью. Однако гораздо бОльшее распространение получила функция распределения случайной величины.
Стандартное обозначение: 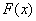
И для дискретной, и для непрерывной случайной величины она определяется одинаково:
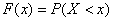 , где
, где 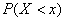 – вероятность того, что случайная величина
– вероятность того, что случайная величина 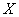 примет значение, МЕНЬШЕЕ, чем переменная
примет значение, МЕНЬШЕЕ, чем переменная 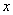 , которая «пробегает» все действительные значения (от «минус» до «плюс» бесконечности).
, которая «пробегает» все действительные значения (от «минус» до «плюс» бесконечности).
Смысл функции распределения хорошо иллюстрирует наша любимая игра:
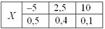
Чему, например, равно значение 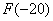 ? Это вероятность того, что выигрыш будет меньше, чем –20. И это невозможное событие:
? Это вероятность того, что выигрыш будет меньше, чем –20. И это невозможное событие: 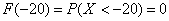 . Совершенно понятно, что
. Совершенно понятно, что 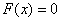 и для всех «икс» из интервала
и для всех «икс» из интервала 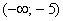 , а также для
, а также для 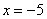 . Почему? По определению функции распределения:
. Почему? По определению функции распределения:
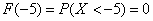 – вы согласны? Функция
– вы согласны? Функция 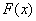 возвращает вероятность того, что в точке
возвращает вероятность того, что в точке 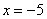 выигрыш будет СТРОГО МЕНЬШЕ «минус» пяти.
выигрыш будет СТРОГО МЕНЬШЕ «минус» пяти.
Таким образом: 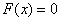 , если
, если 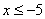 .
.
На интервале 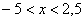 функция
функция 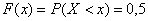 , поскольку левее любой точки этого интервала есть только одно значение
, поскольку левее любой точки этого интервала есть только одно значение 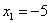 случайной величины, которое появляется с вероятностью 0,5. Кроме того, сюда же следует отнести точку
случайной величины, которое появляется с вероятностью 0,5. Кроме того, сюда же следует отнести точку 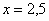 , так как:
, так как:
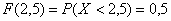 – очень хорошо осознайте этот момент!
– очень хорошо осознайте этот момент!
Таким образом, если 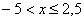 , то
, то 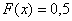
Далее рассматриваем промежуток 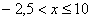 . СТРОГО ЛЕВЕЕ любой точки этого промежутка находятся два выигрыша
. СТРОГО ЛЕВЕЕ любой точки этого промежутка находятся два выигрыша 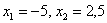 , поэтому:
, поэтому:
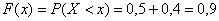
И, наконец, если 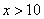 , то
, то 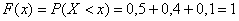 , ибо все значения
, ибо все значения 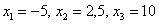 случайной величины
случайной величины 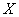 лежат строго левее любой точки
лежат строго левее любой точки 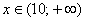
Заметим, кстати, важную вещь: коль скоро, функция 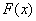 характеризуем вероятность, то она может принимать значения лишь из промежутка
характеризуем вероятность, то она может принимать значения лишь из промежутка 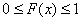 – и никакие другие!
– и никакие другие!
Итак, функция распределения вероятностей ДСВ является кусочной и, как многие знают, в таких случаях принято использовать фигурные скобки:
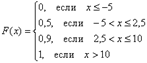
График данной функции имеет разрывный «ступенчатый» вид:

Причём, функция 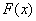 или её график однозначно определяют сам закон распределения:
или её график однозначно определяют сам закон распределения:
– в точке 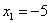 «скачок» разрыва равен 0,5 (следим по чертежу) – и это в точности вероятность
«скачок» разрыва равен 0,5 (следим по чертежу) – и это в точности вероятность 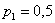 этого значения;
этого значения;
– в точке 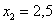 «скачок» составляет
«скачок» составляет 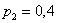 ;
;
– и для выигрыша 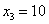 «высота ступеньки» равна
«высота ступеньки» равна 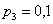 .
.
Таким образом, функция распределения вероятностей – это ещё один способ ЗАДАТЬ случайную величину. И этот способ особо важен для непрерывной случайной величины – по той причине, что её невозможно описать таблицей (ввиду бесконечного и несчётного количества принимаемых значений). Однако, всему своё время.
Сейчас мы освоим технические моменты решения типовой задачи:
Пример 13
Построить функцию распределения случайной величины 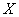
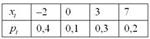
Найти вероятности того, что случайная величина примет значение из следующих промежутков:
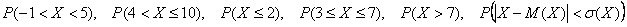
Решение: рассмотрим формальный алгоритм построения функции распределения.
Сначала берём первое значение 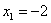 и составляем нестрогое неравенство
и составляем нестрогое неравенство 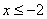 . На этом промежутке
. На этом промежутке 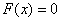 .
.
На промежутке 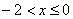 (между
(между  и
и 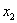 ):
):
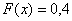
На промежутке 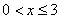 (между
(между 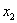 и
и 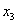 ):
):
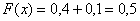
На промежутке 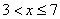 (между
(между 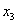 и
и 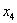 ):
):
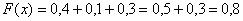
И, наконец, если 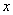 строго больше самого последнего значения
строго больше самого последнего значения 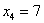 , то:
, то:
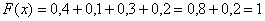
Легко заметить, что с увеличением «икс» идёт накопление (суммирование) вероятностей, и поэтому функцию 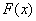 также называют интегральной функцией распределения. В практических задачах проведённые выше действия нужно выполнять в уме, а результат сразу записывать под единую скобку:
также называют интегральной функцией распределения. В практических задачах проведённые выше действия нужно выполнять в уме, а результат сразу записывать под единую скобку:

Выполним чертёж:
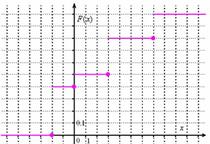
и проконтролируем правильность решения с помощью «скачков» графика: в точке 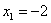 «скачок» равен
«скачок» равен 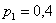 , в точках:
, в точках: 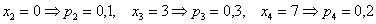
При выполнении чертежа от руки оптимален следующий масштаб:
горизонтальная ось: 1 ед. = 2 или 1 тетрадная клетка;
вертикальная ось: 0,1 = 1 тетрадная клетка.
На левых концах ступенек (кроме нижнего луча) можно ставить выколотые точки – дело вкуса. И ещё хочу остановиться на двух технических ошибках, которые часто допускают на практике. При выполнении чертежа простым карандашом левый нижний луч следует прочерчивать жирно (чтобы он не сливался с координатной осью) и до конца оси! Второй момент: правая верхняя линия не должна заканчиваться раньше острия оси! Такие оплошности могут говорить о непонимании функции распределения, а это, как вы понимаете, скверно.
Переходим ко второй части задания.
Найдём 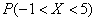 – вероятность того, что случайная величина
– вероятность того, что случайная величина 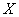 примет значение из интервала
примет значение из интервала 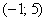 .
.
И здесь я сформулирую практическое правило: если оба конца 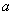 и
и 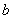 промежутка не «попадают» в точки разрыва функции
промежутка не «попадают» в точки разрыва функции 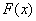 , то следующие вероятности:
, то следующие вероятности: 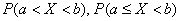 ,
, 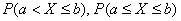 можно найти по единой формуле:
можно найти по единой формуле:
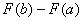
В данном случае концы интервала (–1 и 5) находятся в области непрерывности функции распределения поэтому:
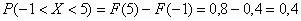
И действительно, на данном интервале находятся значения 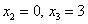 , вероятности появления которых:
, вероятности появления которых: 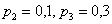 .
.
Вычислим вероятность 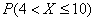 . Оба конца этого промежутка не «попадают» в точки разрыва, поэтому:
. Оба конца этого промежутка не «попадают» в точки разрыва, поэтому:
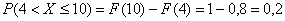 – вероятность того, что случайная величина
– вероятность того, что случайная величина 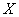 примет значение из данного промежутка. И в самом деле – на нём находится единственное значение
примет значение из данного промежутка. И в самом деле – на нём находится единственное значение 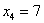 , которое может появиться с вероятностью 0,2.
, которое может появиться с вероятностью 0,2.
Та же самая история с 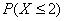 – единственное, тут левый конец промежутка равен «минус» бесконечности:
– единственное, тут левый конец промежутка равен «минус» бесконечности:
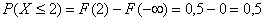 – самостоятельно проанализируйте, какие значения
– самостоятельно проанализируйте, какие значения 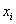 , и с какими вероятностями располагаются на полуинтервале
, и с какими вероятностями располагаются на полуинтервале 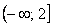
Теперь более занятная ситуация, где нужно особо включать голову: если хотя бы один из концов 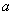 и
и 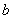 промежутка «попадает» в точку разрыва функции, то указанную выше формулу можно использовать лишь в одном случае из четырёх:
промежутка «попадает» в точку разрыва функции, то указанную выше формулу можно использовать лишь в одном случае из четырёх:
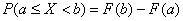
! Примечание: если 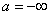 , то левое неравенство становится строгим, но формула тоже применима.
, то левое неравенство становится строгим, но формула тоже применима.
Это равенство строго доказывается в курсе теории вероятностей – перепишите в свой справочник!
Найдём 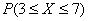 . Как быть? – под правило не подходит! Вспоминаем теоремы тервера. По теореме сложения вероятностей несовместных событий:
. Как быть? – под правило не подходит! Вспоминаем теоремы тервера. По теореме сложения вероятностей несовместных событий:
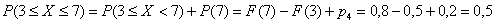 – вероятность того, что случайная величина
– вероятность того, что случайная величина 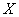 примет значение из отрезка
примет значение из отрезка 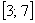 . И действительно, этот отрезок включает в себя два значения
. И действительно, этот отрезок включает в себя два значения 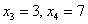 , которые появляются с вероятностями
, которые появляются с вероятностями 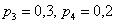 .
.
Тут же рассмотрим три других ситуации:
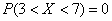 , т.к. на интервале
, т.к. на интервале 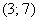 нет значений случайной величины. Да-да, так и пишем.
нет значений случайной величины. Да-да, так и пишем.
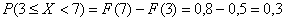 – это «штатный» теоретический случай.
– это «штатный» теоретический случай.
И для 2-го полуинтервала используем теорему сложения вероятностей несовместных событий:
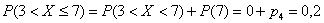
Едем дальше:
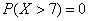 , поскольку там нет значений случайной величины. Кстати, случай с нестрогим неравенством – есть «штатный» случай:
, поскольку там нет значений случайной величины. Кстати, случай с нестрогим неравенством – есть «штатный» случай:
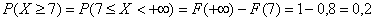
который можно записать и так: 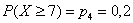 – на функции распределения «свет клином не сошёлся»!
– на функции распределения «свет клином не сошёлся»!
И, наконец, типовая вероятность 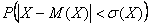 – того, что значение случайной величины
– того, что значение случайной величины 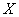 отклонится от своего математического ожидания не более чем на среднее квадратическое отклонение. Как вы догадываетесь, их нужно предварительно вычислить, но эти числовые характеристики уже найдены в Примере 6 статьи о дисперсии:
отклонится от своего математического ожидания не более чем на среднее квадратическое отклонение. Как вы догадываетесь, их нужно предварительно вычислить, но эти числовые характеристики уже найдены в Примере 6 статьи о дисперсии: 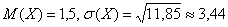 . Раскрываем модуль и пользуемся тем фактом, что концы интервала не «попадают» в точки разрыва функции распределения:
. Раскрываем модуль и пользуемся тем фактом, что концы интервала не «попадают» в точки разрыва функции распределения:
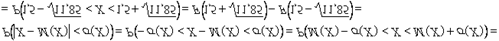
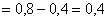 – искомая вероятность.
– искомая вероятность.
Напоминаю, что в типичном случае на интервале 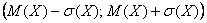 и вблизи него «сконцентрированы» наиболее вероятные значения случайной величины. Так сказать, «центр событий».
и вблизи него «сконцентрированы» наиболее вероятные значения случайной величины. Так сказать, «центр событий».
Ответ:
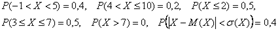
Напоминаю, что для любителей комфорта есть соответствующая программа (см. после Примера 6 ), которая строит графики автоматически; причём результаты её работы элементарно копируются в Вёрд.
И аналогичное задание для самопроверки:
Пример 14
Составить функцию распределения случайной величины 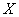

Выполнить чертёж. Найти вероятности следующих событий:
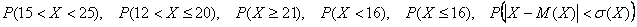
Подумайте над рациональным масштабом графика. Если возникают сомнению с нахождением вероятностей, помните – их всегда можно пересчитать вручную.
Решение и ответ совсем рядом. Кроме того, несколько дополнительных задач есть в библиотеке.
И не успела появиться эта статья, как от читателей сайта стали поступать просьбы включить в неё контрольный пример. Я даже прослезился (прямо как тот профессор), и, конечно же, не мог вам отказать:
Пример 15
В билете три задачи. Вероятность того, что студент правильно решит первую задачу, равна 0,9, вторую – 0,8, третью – 0,7. Составить закон распределения числа правильно решенных задач в билете, вычислить математическое ожидание и дисперсию этой случайной величины. Построить график функции распределения. Найти вероятность того, что студент сдаст зачёт, если для этого нужно правильно решить не менее двух задач.
Проверьте, насколько хорошо вы усвоили материал. Тут нужно использовать теоремы умножения и умножения, и могут возникнуть накладки с обозначениями. В образце решения я обозначил 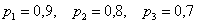 , а вероятности значений случайной величины – через
, а вероятности значений случайной величины – через 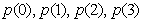 .
.
После чего мы перейдём к изучению непрерывной случайной величины.
Да, наш урок, посвященный дискретной случайной величине, подошел к концу – но это не значит, что тема закрыта!
Вперёд – за новыми открытиями!
Решения и ответы:
Пример 12. Решение: запишем закон распределения случайной величины 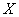 :
:

Контроль: 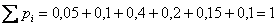
Пример 14. Решение: составим функцию распределения вероятностей:
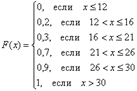
Выполним чертёж:
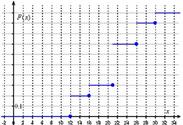
Примечание: сплошная нумерация по оси абсцисс представлена исключительно ради удобства восприятия.
Вычислим вероятности того, что случайная величина 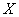 примет значение из предложенных интервалов:
примет значение из предложенных интервалов:
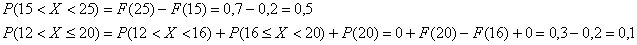
более простой способ:
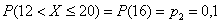
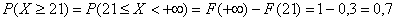 («штатный» случай)
(«штатный» случай)
 (частный случай «штатной» формулы)
(частный случай «штатной» формулы)
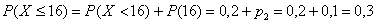
Числовые характеристики 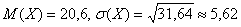 найдены в Примере 8, вычислим вероятность того, что случайная величина
найдены в Примере 8, вычислим вероятность того, что случайная величина 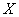 отклонится от математического ожидания не более чем на среднее квадратическое отклонение:
отклонится от математического ожидания не более чем на среднее квадратическое отклонение:
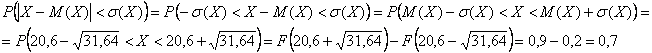
Ответ:
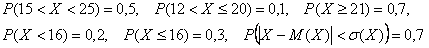
Пример 15. Решение: найдём вероятности того, что соответствующие задачи будут решены неверно:
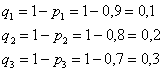
Используя теоремы умножения независимых и сложения несовместных событий, составим закон распределения случайной величины 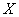 – числа правильно решенных задач в билете:
– числа правильно решенных задач в билете:
0) 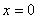 (все задачи решены неверно)
(все задачи решены неверно)
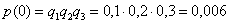
1) 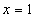
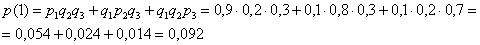
2) 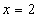
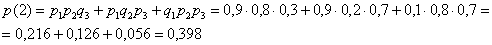
3) 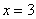 (все задачи решены правильно)
(все задачи решены правильно)
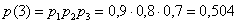
Таким образом, искомый закон распределения:
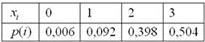
Контроль: 0,006 + 0,092 + 0,398 + 0,504 = 1
Вычислим 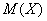 и
и 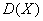 . Заполним расчетную таблицу:
. Заполним расчетную таблицу:
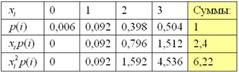
Математическое ожидание: 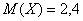
Дисперсия: 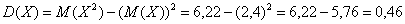 .
.
Составим функцию распределения:
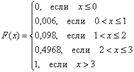
Выполним чертеж:
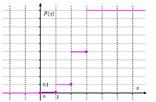
Найдём вероятность  – того, что студент сдаст зачёт:
– того, что студент сдаст зачёт: