Определение: Квадратным уравнением называется уравнение вида
ax^2 + bx + c = 0,
где х – переменная, а, b и с – некоторые числа, причем, а ≠ 0.
Числа а, b и с - коэффициенты квадратного уравнения. Число а называют первым коэффициентом, число b – вторым коэффициентом и число c – свободным членом.
● Пример.
8x^2 – 7x + 3 =0
В каждом из уравнений вида ax^2 + bx + c = 0, где а ≠ 0, наибольшая степень переменной x – квадрат. Отсюда и название: квадратное уравнение.
Квадратное уравнение, в котором коэффициент при х^2 равен 1, называют приведенным квадратным уравнением.
● Пример.
x^2 – 11х+ 30=0, х^2 –8х= 0.
Если в квадратном уравнении ах^2 + bx + c = 0, один из коэффициентов
b или с равен нулю, то такое уравнение называют неполным квадратным уравнением.
Неполные квадратные уравнения бывают трёх видов:
1) ах^2 + с = 0, где с ≠ 0;
2) ах^2 + b х = 0, где b ≠ 0;
3) ах^2 = 0.
● Пример.
– 2х^2 + 7 = 0, b = 0;
3х^2 – 10х = 0, с = 0;
– 4х^2 = 0, b = 0; c = 0.
Способы решения неполных квадратных уравнений.
1. Для решения неполного квадратного уравнения вида ах^2 + с = 0 при с ≠ 0 переносят его свободный член в правую часть и делят обе части уравнения на а. Получается уравнение
х^2 = – 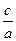 ,
,
равносильное уравнению ах^2 + с = 0.
Так как с ≠ 0, то – 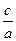 ≠ 0.
≠ 0.
Если – 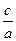 > 0, то уравнение имеет два корня:
> 0, то уравнение имеет два корня:
х 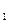 = –
= – 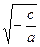 и х
и х 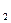 =
= 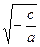 .
.
Если – 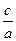 < 0, то уравнение не имеет корней.
< 0, то уравнение не имеет корней.
Пример 1. Рассмотрим уравнение –3х^2 + 15=0.
Перенесем свободный член в правую часть уравнения и разделим обе части получившегося уравнения на –3:
–3х^2 = –15,
x^2 = 5.
Отсюда х 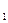 =
= 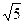 или х
или х 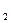 = –
= – 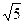
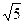 и –
и – 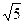 являются корнями уравнения –3х^2 + 15= 0.
являются корнями уравнения –3х^2 + 15= 0.
Пример 2. Рассмотрим уравнение 4х^2 + 3 = 0.
Перенесем свободный член в правую часть уравнения и разделим обе части
получившегося уравнения на 4:
4х^2 = –3,
x^2 = – 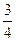 .
.
Так как квадрат числа не может быть отрицательным числом, то получившееся уравнение корней не имеет. Следовательно, равносильное ему уравнение 4х^2 + 3 = 0 не имеет корней.
2. Для решения неполного квадратного уравнения вида ах^2 + bx = 0 при b ≠ 0
раскладывают его левую часть на множители и получают уравнение
х(ах + b)= 0
Произведение х(ах + b)= 0 равно нулю только тогда, когда хотя бы один из множителей равен нулю:
х = 0 или ах + b = 0.
Решая уравнение ах + b = 0, в котором а ≠ 0, находим
a х = – b,
х = – 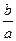 .
.
Следовательно, произведение ах^2 + bx = 0 обращается в нуль при х = 0 и при
х = – 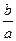 . Корнями уравнения ах^2 + bx = 0 являются числа 0 и –
. Корнями уравнения ах^2 + bx = 0 являются числа 0 и – 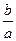 . Значит, неполное квадратное уравнение вида ах^2 + bx = 0 при b ≠ 0 всегда имеет два корня.
. Значит, неполное квадратное уравнение вида ах^2 + bx = 0 при b ≠ 0 всегда имеет два корня.
Пример. Рассмотрим уравнение 4х^2 + 9х = 0.
Разложим левую часть уравнения на множители:
х(4х + 9)= 0.
Отсюда х = 0 или 4х + 9 = 0.
Решим уравнение 4х + 9 = 0:
4х = – 9,
х = –2 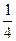 .
.
Ответ: х 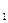 = 0, х
= 0, х 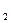 = –2
= –2 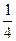 .
.
3. Неполное квадратное уравнение вида ах 2 = 0 равносильно уравнению х 2 = 0 и поэтому имеет один единственный корень 0.
Теорема Виета называется по имени знаменитого французского математика Франсуа Виета.
Используя теорему Виета, можно выразить сумму и произведение корней произвольного квадратного уравнения через его коэффициенты.
Приведенное квадратное уравнение х^2 – 7х + 10 = 0 имеет корни 2 и 5. Сумма корней равна 7, а произведение равно 10. На примере видно, что сумма корней равна второму коэффициенту, взятому с противоположным знаком, а произведение корней равно свободному члену. Необходимо доказать, что любое приведенное квадратное уравнение, имеющее корни, обладает таким свойством.
Теорема: Сумма корней приведенного квадратного уравнения равна второму коэффициенту, взятому с противоположным знаком, а произведение корней равно свободному члену.
Приведенное квадратное уравнение имеет вид:
x^2 + bx + c = 0.
Обозначим второй коэффициент буквой р, а свободный член буквой q:
x^2 + px + q = 0.
Дискриминант этого уравнения D равен p^2 – 4q.
Пусть D > 0. тогда это уравнение имеет два корня:
х 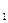 =
=  и х
и х  =
= 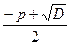 .
.
Найдем сумму и произведение корней:
х 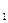 + х
+ х  =
= 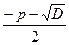 +
+ 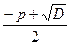 =
= 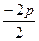 = –p;
= –p;
х 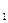 ∙ х
∙ х  =
=  ∙
∙ 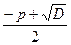 =
= 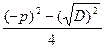 =
= 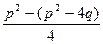 =
= 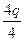 = q.
= q.
Следовательно,
х 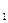 + х
+ х  = –p, х
= –p, х 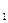 ∙ х
∙ х  = q.
= q.
Пример. Рассмотрим уравнение х^2 – 3х + 2 = 0.
D =1, уравнение имеет два корня. х1 = 2 и х2 = 1, p = –3; q = 2.
По теореме Виета х 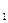 + х
+ х  = – p, значит 2 + 1= 3;
= – p, значит 2 + 1= 3;
х  ∙ х
∙ х  = q, значит 2 ∙ 1= 2.
= q, значит 2 ∙ 1= 2.
Следовательно х1 = 2 и х2 = 1 являются корнями уравнения х^2 – 3х + 2 = 0.
При D = 0 корни уравнения можно вычислить по формуле
х = 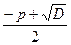 и x =
и x = 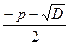 .
.
Квадратное уравнение ax^2 + bx + c = 0 имеет корни х  и х
и х 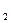 . равносильное ему приведенное квадратное уравнение имеет вид
. равносильное ему приведенное квадратное уравнение имеет вид
х 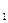 + х
+ х  = –
= –  , х
, х 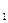 ∙ х
∙ х  =
= 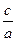 .
.
Справедливо утверждение, обратное теореме Виета:
Теорема: Если числа m и n таковы, что их сумма равна –p, а произведение
равно q, то эти числа являются корнями уравнения х^2 + px + q = 0.
По условию т + п = – p, а т п = q. Значит, уравнение х^2 + px + q = 0 можно записать в виде
х^2 – (т + п) х + т п= 0.
Подставив вместо х число т, получим:
т^2 – (т + п) т + т п = т^2 – т2 – т п + т п = 0.
Значит, число т является корнем уравнения.
Аналогично можно показать, что число п также является корнем уравнения.
Пример. Рассмотрим уравнение х^2 + 3х – 40=0.
D = 32 +4 ∙40= 169.
По формуле корней квадратного уравнения получаем
х  =
= 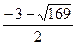 ; х
; х  =
= 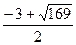 .
.
Отсюда х  = –8; х
= –8; х  = 5.
= 5.
Покажем, что корни уравнения найдены правильно. В уравнении
x^2 + 3х – 40=0 коэффициент р равен 3, а свободный член q равен –40. Сумма найденных чисел –8 и 5 равна –3, а их произведение равно –40. Значит, по теореме, обратной теореме Виета, эти числа являются корнями уравнения х^2 + 3х – 40=0.