Оглавление
Введение. 3
Теория линейного программирования. 4
Решение. 6
Заключение. 8
Список используемой литературы.. 9
Введение
Математические теории и методы сейчас проникли во все другие науки, начиная с биологии и психологии и кончая лингвистикой. Вряд ли можно указать сферу практической и духовной деятельности человека, где бы ни применялись методы математического исследования. Если ранее математический аппарат преимущественно использовался как инструмент расчёта, то теперь ставится задача выбора наиболее эффективного решения проблемы, поиск оптимального варианта. Такого типа задачи привели к возникновению новых математических дисциплин: линейного и нелинейного программирования, теории массового обслуживания, теории игр, теории очередей и т.д.
Постановка задачи линейного программирования впервые прозвучала в работах российского экономиста А.Н. Толстого при составлении плана перевозки груза между пунктами так, чтобы общий пробег транспорта был наименьшим. Математические основы для решения задач линейного программирования были созданы в 1939 году академиком Л.В. Канторовичем и его учениками. Методы линейного программирования получили широкое распространение при решении экономических задач, в планировании производства, в сельском хозяйстве, в военном деле. Их значимость подчёркивается тем, что они реализованы в прикладных компьютерных программах (MS Excel) и могут использоваться при необходимости каждым, кто умеет работать на ПК.
Теория линейного программирования
Как известно, в практике хозяйственной деятельности выбор между различными вариантами (планами, решениями) предполагает поиск наилучшего. Когда хозяйка отправляется на рынок для закупки мяса, а проектировщик стремится найти оптимальный способ размещения станков, они занимаются поисками вариантов, требующих минимума затрат или максимума результата с учетом определенных ограничений (денег, ресурсов, времени).
Решить подобную задачу бывает непросто, особенно при наличии большого числа вариантов. Время и затраты при выборе оптимума не всегда оправданны: издержки поиска и перебора вариантов могут превысить достигнутый выигрыш. Как показывает практика, опыт и интуиция оказываются недостаточными для обоснования оптимального решения. Более надежный и эффективный способ — использование математических (количественных) подходов и расчетов. Однако математические подходы и обоснования длительное время игнорировались теоретиками, делавшими “погоду” в экономической науке. Многие важные работы были заморожены, публикации экономистов-математиков тормозились и ограничивались. И все же в тот период математические изыскания продолжались, даже в условиях гонения на математиков были достигнуты блестящие результаты. Одним из наиболее значительных и ярких достижений в области экономико-математических исследований было открытие Леонидом Витальевичем Канторовичем (1912—1986) Метода линейного программирования.
Линейное программирование — решение линейных уравнений (уравнений первой степени) посредством составления программ и применения различных методов их последовательного решения, существенно облегчающих расчеты и достижение искомых результатов.
Задачи линейного программирования можно решать двумя методами: графическим, если задача содержит только два неизвестных, и симплекс-методом, если в задаче более двух неизвестных. Подавляющее большинство практических задач содержит значительно более двух неизвестных, поэтому симплекс-метод наиболее актуален. Для старшеклассников, с их сравнительно небольшим жизненным опытом, одним из интересных и сложных моментов является составление математической модели экономической задачи. При этом им приходится знакомиться с новыми экономическими понятиями, специальной терминологией той отрасли хозяйства, с которой связана проблема. Математическая модель задачи представляет собой систему ограничений (она состоит из уравнений и/или неравенств), накладываемых на неизвестные и отражающую взаимосвязь между этими неизвестными, а также целевую функцию – зависимость оптимизируемого параметра от неизвестных. Целевую функцию надо максимизировать (получить наибольшую прибыль) или минимизировать (ограничить потребление питательных веществ только необходимым их количеством для нормальной жизни).
Симплекс-метод реализуется в три этапа:
- 1 этап – запись задачи в таблицу;
- 2 этап – определение допустимого решения;
- 3 этап – определение оптимального решения.
Для решения задачи симплексным методом система ограничений и целевая функция сначала записываются в таблицу определённым образом, а затем способом преобразования таблиц с разрешающим элементом неизвестные выражаются через свободные члены. Такой способ позволяет значительно рационализировать вычисления, формализовать процесс решения и значительно сократить количество записей. На третьем этапе нахождения оптимального решения проводятся заключительные преобразования таблицы по определённому правилу и результат готов (крайний правый столбец таблицы).
Для примера приведу решение задачи о диете.
Для откорма животных на ферме в их еженедельный рацион необходимо включать не менее 33 ед. питательного вещества А, 23 ед. питательного вещества В и 12 ед. питательного вещества С. Для откорма используется 3 вида кормов. Данные о содержании питательных веществ и стоимость одной весовой единицы каждого из кормов помещены в таблице:
| А | В | С | Стоимость 1 ед. | |
| В 1 ед. корма 1 | 4 ед. | 3 ед. | 1 ед. | 20 руб. |
| В 1 ед. корма 2 | 3 ед. | 2 ед. | 1 ед. | 20 руб. |
| В 1 ед. корма 3 | 2 ед. | 1 ед. | 2 ед. | 10 руб. |
Составить наиболее дешёвый рацион, при котором каждое животное получало бы необходимые количества питательных веществ А, В, С.
Решение
Обозначим через х1, х2, х3 количества кормов 1, 2 и 3 видов соответственно, включаемых в еженедельный рацион. Тогда каждое животное получит (4х1 + 3х2 + 2х3) ед. вещества А и это число не должно быть меньше 33, т.е. 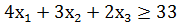
Питательного вещества В каждое животное получит (3х1 + 2х2 + х3 ) ед. и питательного вещества С – (х1 + х2 + 2х3) ед. и эти количества не должныбыть меньше соответственно 23 и 12. При таком расходовании кормов стоимость еженедельного рациона будет Z = 20х1 + 20х2 + 10х3
Запишем задачу в таблицу:
| Х1 | Х2 | Х3 | ||
| У1 = | -33 | |||
| У2 = | -23 | |||
| У3 = | -12 | |||
| Z = |
Определяем допустимые решения путём преобразования таблиц с разрешающими элементами (выделены курсивом)
| Х1 | Х2 | у2 | ||
| У1 = | -2 | -1 | ||
| х3 = | -3 | -2 | ||
| У3 = | -5 | -3 | ||
| Z = | -10 |
Находим оптимальное решение
| Х1 | Х2 | у2 | ||
| У1 = | -2 | -1 | ||
| х3 = | -3 | -2 | ||
| У3 = | -5 | -3 | ||
| Z = | -10 |
| у1 | Х2 | у2 | ||
| х1= | 13/2 | |||
| х3 = | 7/2 | |||
| У3= | 3/2 | |||
| Z = |
Ответ: х1 = 6,5; х2 =0; х3 = 3,5; стоимость еженедельного рациона 165 руб.
Заключение
Описанная в исследовательской работе задача линейного программирования и методы ее решения – только отдельный пример огромного множества задач линейного программирования. Особенностью задач линейного программирования является то, что экстремума целевая функция достигает на границе области допустимых решений. Классические же методы дифференциального исчисления связаны с нахождением экстремумов функции во внутренней точке области допустимых значений. Линейное программирование представляет собой наиболее часто используемый метод оптимизации. Линейное программирование является одной из основных частей того раздела современной математики, который получил название математического программирования. Задачи линейного программирования решаются несколькими методами. При построении симплексного метода предполагалось, что все опорные планы невырожденные, что обеспечивало получение оптимального плана за конечное количество шагов. В случае вырожденного плана вычисления производят аналогично, но в этом случае возможен возврат к старому базису, что приводи к так называемому зацикливанию. В основу модифицированного симплекс – метода положены такие особенности линейной алгебры, которые позволяют в ходе решения задачи работать с частью матрицы ограничений. Иногда метод называют методом обратной матрицы. В целом, метод отражает традиционные черты общего подхода к решению задач линейного программирования, включающего в себя канонизацию условий задачи, расчёт симплекс-разностей, проверку условий оптимальности.
СПИСОК ИСПОЛЬЗУЕМОЙ ЛИТЕРАТУРЫ
1. Акулич И.Л. Математическое программирование в примерах и задачах: учеб.пособие для ВУЗов / И. Л. Акулич. – М.: Высшая школа, 1986.
2. Гончаров Е. Н. Исследование операций. Примеры и задачи: учеб.пособие / Е. Н. Гончаров, А. И. Ерзин, В. В. Залюбовский. –Н.: Гос. ун-т. Новосибирск, 2005.
3. Павлова Т. Н. Линейное программирование: учеб.пособие / Т. Н. Павлова, О. А. Ракова. – Д.: 2002.
4.БерюховаТ.Н.Банк производственных задач в расчетах на ЭВМ: учебное пособие. –Тюмень.: ТюмИИ, 1992. – 124с.
Карманов В.Г. Математическое программирование: учебное пособие для студентов вузов. – М.: Физматлит, 2001. – 264с.
5. Кузнецов А.В. Математическое программирование: учебное пособие для вузов. – М.: Высшая школа, 1976. – 352с.
6. Мочалов И.А. Нечеткое линейное программирование. // Промышленные АСУ и контроллеры. – 2006. - № 10. – с.26-29.
7. Пашутин С. Оптимизация издержек и технология формирования оптимального ассортимента. // Управление персоналом. – 2005. - №5. – с.20-24.
8.Жиглявский А.А., Жилинкас А.Г. Методы поиска глобального экстремума. — М.: Наука, Физматлит, 1991.
9. Карманов В.Г. Математическое программирование = Математическое программирование. — Изд-во физ.-мат. литературы, 2004.
10. Корн Г., Корн Т. Справочник по математике для научных работников и инженеров. — М.: Наука, 1970. — С. 575-576.