МОСКОВСКИЙ ГОСУДАРСТВЕННЫЙ СТРОИТЕЛЬНЫЙ УНИВЕРСИТЕТ
_
Кафедра высшей математики
ТЕОРИЯ ПРЕДЕЛОВ
МЕТОДИЧЕСКИЕ УКАЗАНИЯ
К ПРАКТИЧЕСКИМ ЗАНЯТИЯМ И
ВЫПОЛНЕНИЮ РАСЧЕТНОГО ЗАДАНИЯ
ДЛЯ СТУДЕНТОВ ЗАОЧНОГО ОТДЕЛЕНИЯ
Москва 2007
С о с т а в и т е л и:
доцент, кандидат физико-математических наукВ.Н.Борзунов
Примеры решения задач по теории пределов
Основные определения
Определение 1. Число A называется пределом последовательности  , если для любого
, если для любого 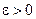 можно вычислить число
можно вычислить число  (зависящее от ε) такое, что для всех натуральных
(зависящее от ε) такое, что для всех натуральных 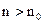 выполняется
выполняется 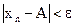 .
.
В этом случае пишут  или
или  и говорят, что последовательность
и говорят, что последовательность  сходится к числу A.
сходится к числу A.
Пример.1. Используя определение предела последовательности, доказать, что  .
.
◄ Возьмем произвольное число 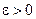 . Если будет найдено такое число
. Если будет найдено такое число  , что для всех натуральных
, что для всех натуральных 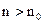 будет выполняться неравенство
будет выполняться неравенство 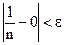 , то это значит, что
, то это значит, что  . Рассмотрим
. Рассмотрим 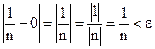 . Умножаем левую и правую часть неравенства на n и на
. Умножаем левую и правую часть неравенства на n и на  , учитываем, что n>0 и
, учитываем, что n>0 и 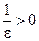 , знак неравенства не изменится. Получаем, что
, знак неравенства не изменится. Получаем, что 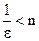 . Таким образом, за число
. Таким образом, за число  можно принять число
можно принять число  или любое другое число, большее, чем
или любое другое число, большее, чем  . При всех натуральных
. При всех натуральных 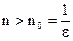 , выполняется
, выполняется 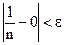 , следовательно
, следовательно  .
.
Пример.2. Используя определение предела последовательности, доказать, что  .
.
◄ Возьмем произвольное число 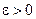 . Рассмотрим
. Рассмотрим 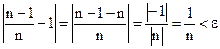 . Умножаем левую и правую часть неравенства на n и на
. Умножаем левую и правую часть неравенства на n и на  , учитываем, что n>0 и
, учитываем, что n>0 и 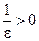 , знак неравенства не изменится. Получаем, что
, знак неравенства не изменится. Получаем, что 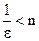 . Таким образом,
. Таким образом, 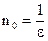 При всех натуральных
При всех натуральных 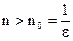 , выполняется
, выполняется  , следовательно
, следовательно  .
.
Пример.3. Используя определение предела последовательности, доказать, что  .
.
◄ Возьмем произвольное число 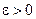 . Если будет найдено такое число
. Если будет найдено такое число  , что для всех натуральных
, что для всех натуральных 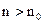 будет выполняться неравенство
будет выполняться неравенство 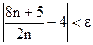 , то это значит, что
, то это значит, что  . Рассмотрим
. Рассмотрим 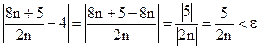 . Умножаем левую и правую часть неравенства на n и на
. Умножаем левую и правую часть неравенства на n и на  , учитываем, что n>0 и
, учитываем, что n>0 и 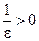 , знак неравенства не изменится. Получаем, что
, знак неравенства не изменится. Получаем, что 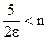 . Таким образом, за число
. Таким образом, за число  можно принять число
можно принять число 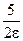 или любое другое число, большее, чем
или любое другое число, большее, чем 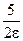 . При всех натуральных
. При всех натуральных  , выполняется
, выполняется 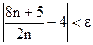 , следовательно
, следовательно  .
.
Определение 2. Число A называется пределом функции f(x) в точке a, если для любого 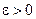 можно вычислить число
можно вычислить число  (зависящее от ε) такое, что для всех x, для которых
(зависящее от ε) такое, что для всех x, для которых 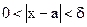 , выполняется
, выполняется 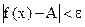 .
.
В этом случае пишут 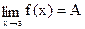 или f(x)→A при x→a и говорят, что предел функции f(x) в точке a существует и равен числу A.
или f(x)→A при x→a и говорят, что предел функции f(x) в точке a существует и равен числу A.
Пример.4. Используя определение предела функции, доказать, что  .
.
◄ Возьмем произвольное число 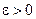 . Если будет найдено число δ(ε)>0 такое, что для всех x, удовлетворяющих неравенству
. Если будет найдено число δ(ε)>0 такое, что для всех x, удовлетворяющих неравенству  , будет справедливо неравенство
, будет справедливо неравенство 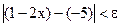 , то это значит, что
, то это значит, что  . Рассмотрим
. Рассмотрим 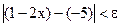



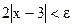

 . Таким образом, за число δ можно принять число
. Таким образом, за число δ можно принять число 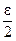 или любое другое положительное число, меньшее, чем
или любое другое положительное число, меньшее, чем 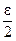 . При всех x, для которых справедливо
. При всех x, для которых справедливо 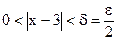 , выполняется
, выполняется 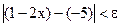 , следовательно
, следовательно  .
.
Определение 3. Число A называется пределом функции f(x) в точке a слева, если для любого  можно вычислить число
можно вычислить число  (зависящее от ε) такое, что для всех x, для которых
(зависящее от ε) такое, что для всех x, для которых 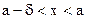 , выполняется
, выполняется 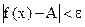 .
.
В этом случае пишут  или f(x)→A при x→a–o и говорят, что предел функции f(x) в точке a слева существует и равен числу A.
или f(x)→A при x→a–o и говорят, что предел функции f(x) в точке a слева существует и равен числу A.
Определение 4. Число A называется пределом функции f(x) в точке a справа, если для любого 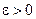 можно вычислить число
можно вычислить число  (зависящее от ε) такое, что для всех x, для которых
(зависящее от ε) такое, что для всех x, для которых 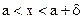 , выполняется
, выполняется 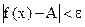 .
.
В этом случае пишут 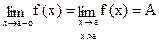 или f(x)→A при x→a+o и говорят, что предел функции f(x) в точке a справа существует и равен числу A.
или f(x)→A при x→a+o и говорят, что предел функции f(x) в точке a справа существует и равен числу A.
Определение 5. Число A называется пределом функции f(x) при x→–∞, если для любого  можно вычислить число xo=xo(ε) (зависящее от ε) такое, что для всех x<xo, выполняется
можно вычислить число xo=xo(ε) (зависящее от ε) такое, что для всех x<xo, выполняется 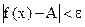 .
.
В этом случае пишут  или f(x)→A при x→–∞ и говорят, что предел функции f(x) при x→–∞ существует и равен числу A.
или f(x)→A при x→–∞ и говорят, что предел функции f(x) при x→–∞ существует и равен числу A.
Определение 6. Число A называется пределом функции f(x) при x→+∞, если для любого  можно вычислить число xo=xo(ε) (зависящее от ε) такое, что для всех x>xo, выполняется
можно вычислить число xo=xo(ε) (зависящее от ε) такое, что для всех x>xo, выполняется 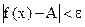 .
.
В этом случае пишут 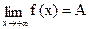 или f(x)→A при x→+∞ и говорят, что предел функции f(x) при x→+∞ существует и равен числу A.
или f(x)→A при x→+∞ и говорят, что предел функции f(x) при x→+∞ существует и равен числу A.
Пример.5. Используя определение предела функции, доказать, что  .
.
◄ Возьмем произвольное число 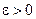 . Если будет найдено число xo(ε) такое, что для всех x>xo, будет справедливо неравенство
. Если будет найдено число xo(ε) такое, что для всех x>xo, будет справедливо неравенство  , то это значит, что
, то это значит, что  Рассмотрим
Рассмотрим 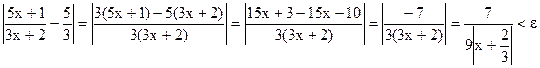
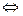
 . Неравенство имеет два решения:
. Неравенство имеет два решения: 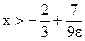 или
или  . Поскольку вычисляется предел f(x) при x→+∞, то выбираем первое решение xo=
. Поскольку вычисляется предел f(x) при x→+∞, то выбираем первое решение xo= 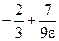 . При всех x>xo, выполняется
. При всех x>xo, выполняется  , следовательно
, следовательно 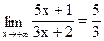 . Второе решение
. Второе решение 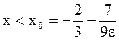 соответствует значениям x→–∞, предел f(x) при x→–∞ также равен
соответствует значениям x→–∞, предел f(x) при x→–∞ также равен 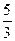 ,
,  .
.
Некоторые свойства пределов функций
Пусть: C постоянное число,
предел функции f(x) существует в точке a, 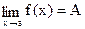 ,
,
предел функции g(x) существует в точке a, 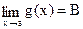 .
.
Тогда:  ,
,
 ,
,
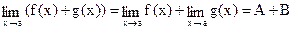 ,
,
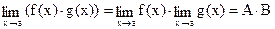 ,
,
 , если
, если  .
.
Предел постоянной величины равен значению этой величины. При вычислениях, константу можно и рекомендуется выносить за знак предела. В условии, когда функции f(x) и g(x) имеют конечные пределы в точке, функции f(x)+g(x), f(x)∙g(x) также имеют пределы в этой точке. При дополнительном условии  , существует предел функции f(x)/g(x).
, существует предел функции f(x)/g(x).
Указанные свойства пределов функций будут соответственно справедливы в точке a слева (x→a–o), в точке a справа (x→a+o), при x→–∞ и при x→+∞.
Эквивалентные функции
Определение 7. Функции f(x) и g(x) называются эквивалентными при x→a, если 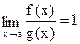 .
.
В этом случае пишут f(x) ~ g(x) при x→a и говорят, что при x→a функция f(x) асимптотически ведет себя как функция g(x) и наоборот, функция g(x) асимптотически ведет себя как функция f(x). При вычислении пределов с использованием эквивалентных функций применяют следующие теоремы:
1. Пусть f(x) ~ g(x) при x→a, тогда 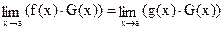 , если один из этих пределов существует.
, если один из этих пределов существует.
2. Пусть f(x) ~ f1(x) и g(x) ~ g1(x) при x→a, тогда 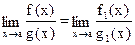 , если один из этих пределов существует.
, если один из этих пределов существует.
Можно сравнивать функции f(x) и g(x) в точке a слева (x→a–o), в точке a справа (x→a+o), при x→–∞ и при x→+∞, при этом вычисляют пределы в соответствующих предельных точках. Например, если 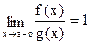 , то говорят, что функции f(x) и g(x) эквивалентны в точке a слева и при x→a–o функция f(x) асимптотически ведет себя как функция g(x). Если
, то говорят, что функции f(x) и g(x) эквивалентны в точке a слева и при x→a–o функция f(x) асимптотически ведет себя как функция g(x). Если  , то говорят, что функции f(x) и g(x) эквивалентны при x→+∞ и пишут f(x) ~ g(x) при x→+∞.
, то говорят, что функции f(x) и g(x) эквивалентны при x→+∞ и пишут f(x) ~ g(x) при x→+∞.
§4. Таблица эквивалентных функций при x→0
1. sin(x) ~ x; 6. ax ~ 1+x∙ln(a); 11. sh(x) ~ x, 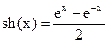 ;
;
2. cos(x) ~ 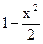 ; 7. ex ~ 1+x; 12. ch(x) ~
; 7. ex ~ 1+x; 12. ch(x) ~  ,
, 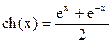 ;
;
3. tg(x) ~ x; 8. loga(1+x) ~  ; 13. th(x) ~ x,
; 13. th(x) ~ x, 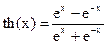 ;
;
4. arcsin(x) ~ x; 9. ln(1+x) ~ x;
5. arctg(x) ~ x; 10. (1+x)α ~ 1+α∙x.