Тема 6. НЕПРЕРЫВНАЯ СЛУЧАЙНАЯ ВЕЛИЧИНА
Другой тип случайных величин, кардинально отличающийся от дискретных, — непрерывные случайные величины.
• Непрерывная случайная величина — это случайная величина, бесконечное и несчетное множество значений которой есть некоторый интервал (конечный или бесконечный) и она сплошь заполняет этот интервал.
Следовательно, закон распределения непрерывной случайной величины нельзя задать рядом распределения. Для этого используются интегральная и дифференциальная функции распределения.
Функция распределения непрерывной случайной величины
Напомним, что функция распределения (интегральная функция) (1.33) определяет вероятность того, что случайная величина X примет значение, меньшее фиксированного действительного числа х: F(x)=Р(Х<х).
• Функция распределения непрерывной случайной величины Х F(x) непрерывна в любой точке и имеет всюду (кроме, возможно, конечного числа точек) непрерывную производную.
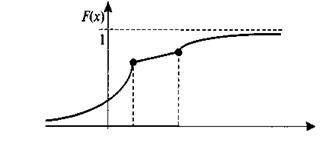
На рис. 9 приведен пример функции распределения непрерывной случайной величины X, которая непрерывна в любой точке и дифференцируема всюду, кроме 2-х точек — 
и 
.
0 х
Рис. 9. Функция распределения некоторой непрерывной случайной величины Х
Теорема.
Вероятность любого отдельно взятого значения непрерывной случайной величины равна нулю.
Доказательство.
Свойства интегральной функции распределения непрерывной случайной величины.
1. Функция распределения может принимать любые значения от 0 до 1, так как по определению является вероятностью:
.
2. Интегральная функция распределения является неубывающей:
.
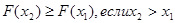3. Для непрерывной случайной величины (согласно приведенной выше теореме):
.
4. Вероятность попадания непрерывной случайной величины в интервал 
равна приращению функции распределения в этих точках:
.
5. Если все возможные значения случайной величины X принадлежат интервалу 
, то
,
.
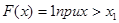6. Если все возможные значения непрерывной случайной величины Х расположены на всей числовой оси ОХ, то
,
.
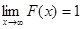Функция плотности вероятности непрерывной случайной величины
Способ задания непрерывной случайной величины с помощью функции распределения не является единственным.
Необходимо определить некоторую функцию, отражающую вероятности попадания случайной точки в различные участки области возможных значений непрерывной случайной величины, т. е. представить некоторую замену вероятностям 
для дискретной случайной величины в непрерывном случае.
Вероятность любого отдельно взятого значения непрерывной случайной величины равна нулю согласно выше доказанной теореме. Поэтому необходимо рассматривать вероятность попадания в некоторый интервал.
Рассмотрим вероятность попадания случайной точки на элементарный участок 
длины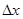 
непрерывной случайной величины X, имеющей непрерывную и дифференцируемую функцию распределения F(x) на этом участке. По 4 свойству функции распределения: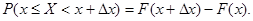 
Определим теперь отношение этой вероятности к длине участка, т. е. среднюю вероятность, приходящуюся на единицу длины рассматриваемого участка, и рассмотрим предел при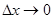 
:
.
Эта функция, характеризующая плотность, с которой распределяются значения непрерывной случайной величины в данной точке, и была названа функцией плотности распределения или функцией плотности вероятностей.
• Плотностью вероятности (плотностью распределения, дифференциальной функцией) случайной величины X называется функция f(х), являющаяся первой производной интегральной функции распределения.
. (1.39)
Под элементом вероятности для случайной величины X понимается величина f(x)dx, с точностью до бесконечно малых величин высшего порядка отражающая вероятность попадания случайной точки X в элементарный отрезок примыкающий к точке х.
Свойства функции плотности вероятностей:
1. Функция плотности вероятностей принимает только неотрицательные значения как производная неубывающей функции распределения F(x):
.
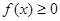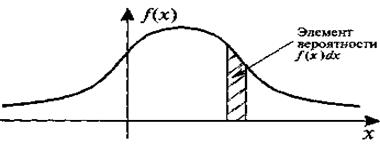
х х+dx
Рис. 10. Функция плотности вероятностей некоторой непрерывной случайной величины Х
2. Вероятность попадания непрерывной случайной величины в интервал от 
до равна определенному интегралу от функции плотности вероятностей в этих пределах:
.
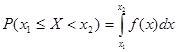0
Рис. 11. Вероятность попадания непрерывной случайной величины Х в интервал
3. Функция распределения непрерывной случайной величины равна интегралу от функции плотности вероятностей в пределах от 
до х:
.
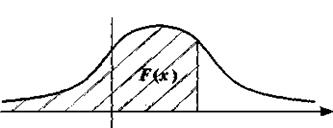
0 х
Рис. 12. Вычисление функции распределения непрерывной случайной величины Х через ее функцию плотности вероятностей
4. Интеграл в бесконечных пределах от функции плотности вероятностей равен 1 (как сумма вероятностей всех возможных значений случайной величины Х):
.
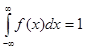0 х
Рис. 13. Под кривой функции плотности вероятностей всегда лежит единичная площадь