Поле событий
Событием будем называть результат (исход) испытания.
Каждое событие происходит при наличии некоторых условий, которые называют комплексом условий.
Пример: Если воду при нормальном давлении нагреть выше 100 градусовС (комплекс условий), то она обращается в пар (событие).
Испытанием называют ситуацию, когда реализуется комплекс условий.
Событие бывает:
достоверным, если оно происходит при каждом испытании.
невозможным, если оно не может происходить при испытаниях.
случайным, если при испытаниях оно то происходит, то не происходит.
Событие В называют противоположным некоторому событию А, если оно заключается в том, что событие А не произошло.
Событие А влечет за собой В, если при наступлении А происходит и В.
Если А влечет за собой В, а В влечет за собой А, то такие события называются равносильными.
Все невозможные события равносильны, обозначаются V.
Все достоверные события равносильны, обозначаются U.
Событие, заключающееся в том, что одновременно произошли события А и В, называется произведением событий А и В.
Событие, заключающееся в том, что произошло одно из событий А или В, называется суммой событий А и В.
Событие, заключающееся в том, что произошло событие А, но не произошло событие В, называется разностью событий А и В.
События А и В называются несовместными, если их одновременное наступление невозможно. (А*В=V)
Если U = В1 + В2 + … + Вn и Bi * Bj = V, то имеем полную группу событий.
Теория вероятностей имеет дело с некоторыми комплексами условий и связанной с ними системой событий S. Будем считать, что для любых событий из S, их произведение, сумма, разность присутствует в S. В S имеются так же и U, и V. Система S, обладающая перечисленными свойствами, называется полем событий.
Классическое определение вероятности
Рассмотрим полную группу событий N = А1+А2+…+Аn. Пусть все Ai равновозможны.
Равновозможность означает, что не существует никаких объективных причин, из-за которых одно из событий Аi должно наступать чаще, чем другое.
Составим полную группу S для этих событий.
(Для полной группы из трех событий A,B,C, получается поле {V, A, B, C, A+B, A+C, B+C, U=A+B+C } из 8 событий.)
Если событие А подразделяется на m частных случаев, входящих в полную группу из n попарно-несовместных равновозможных событий, то вероятностью события А называют число Р(А)=m/n.
Вероятность – функция от А, определенная на S.
Для выяснения, произойдет или не произойдет событие А следует провести испытание, которое даст ответ.
Классическое определение работает, когда исходы равновозможны, определяется общее число исходов проводимого испытания и количество исходов, когда исследуемое событие происходит.
Из определения можно получить свойства вероятностей:
*) 0<=P(A)<=1 P(U)=1 P(V)=0
*) теорема: Если A=B+C и B*C=V, то P(A)=P(B)+P(C)
== Рассматриваем поле событий, содержащее события B и C, а следовательно и A. Пусть для n возможных исходов в поле, m исходов благоприятны событию B и k исходов благоприятны событию C. Тогда событию B+C соответствует m+k исходов.
P(A) = (m+k)/n = m/n + k/n = P(B)+P(C). ==
Методом математической индукции можно распространить теорему на любое число попарно-несовместных слагаемых.
*) теорема: Если А влечет за собой В, то P(A)<=P(B).
== B=A+(~A)*B ==> P(B)=P(A)+P(~A*B) ==> P(B)>=P(A). ==
Геометрическая вероятность. Задача Бюффона
Классическое определение вероятности содержит ряд ограничений и не всегда применимо.
Пусть имеем область G, внутри которой есть область g. Каждой точке области G ставится в соответствие комплекс условий, а каждой точке g – наступление события. Вероятностью этого события будем считать отношение площади области g к площади области G.
В тех случаях, когда применимо классическое определение, оба приводят к одинаковому значению.
Пример несовпадения: В классическом определении если P(A)=0, то A=V. Пусть G –некоторая область, а g – линия внутри этой области. Отношение площади линии к площади области равно 0, однако попадание точки на линию не является невозможным событием.
Задача: Два человека, A и B, договорились встретиться между 12 и 13 часами. Определить вероятность встречи, если пришедший первым ждет 20 минут и уходит.

| Отложим по горизонтальной оси интервал времени с 12 до 13 часов – возможное время прихода A, аналогично, но по вертикальной оси – время прихода B. 20 минут составляют треть часа, разобьем часовые отрезки на 3 части. Закрашенная полоса соответствует случаям, когда встреча произошла. Искомая вероятность равна отношению площади закрашенной фигуры (квадрат без двух треугольников) к площади всего квадрата. Вычисления дают:  = = 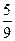
|
Задача Бюффона: На плоскости проведены параллельные прямые на расстоянии 2a друг от друга. На эту плоскость бросают иглу (отрезок) длины 2l (l<a). Какова вероятность того, что игла пересечет хотя бы одну из прямых?
== Положение иглы определяется расстоянием x от центра до ближайшей прямой и углом ф; (0<=x<=a, 0<= ф <=Pi). Если игла пересечет прямую, то x<=l*sin ф.
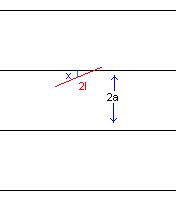
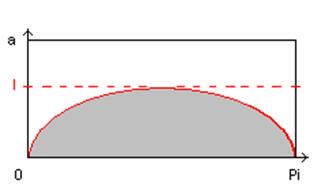
Строим график функции y=l*sin x; 0<x<Pi. Случаю, когда игла пересечет линию, соответствует точка ниже графика, всем возможным точкам соответствует указанный прямоугольник
P =  =
= 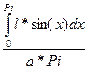 =
= 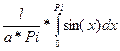 =
= 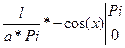 =
= 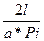 ==
==