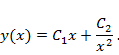Однородным уравнением Эйлера называется линейное однородное уравнение с переменными коэффициентами, имеющее вид
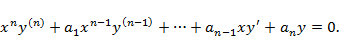
Такое уравнение сводится к уравнению с постоянными коэффициентами с помощью подстановки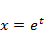 
, где t – новая независимая переменная. Другой способ решения уравнений Эйлера – поиск частных решений вида 
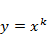. Подстановка этой формулы в исходное уравнение приводит к алгебраическому уравнению n- й степени относительно k. Если все корни последнего уравнения вещественны и различны, они определяют фундаментальную систему решений исходного ОДУ.
Решение типовых задач
Задача 1. Исследовать систему функций на линейную зависимость.
a1) 
Решение. Система линейно зависима по признаку 1.
a2) 
Решение. Система линейно зависима по признаку 2, поскольку 
a3) 
Решение 1 (по определению линейной зависимости). Предположим, что для некоторых чисел 
выполняется тождество 
Подставим в это тождество подходящие значения x и получим систему линейных алгебраических уравнений на неизвестные коэффициенты.
Отсюда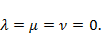 
Таким образом, функции линейно независимы.
Решение 2 (по теореме 1). Составим и вычислим определитель Вронского, разложив его по третьему столбцу:
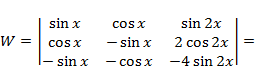
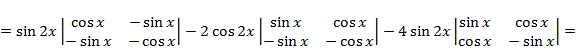
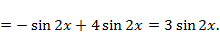
Так как 
функции линейно независимы.
b1)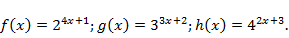 
Решение. Заметим, что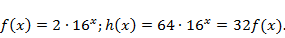 
Функции линейно зависимы.
c1) 
Решение. Функции не пропорциональны, так как множества их нулей не совпадают. Следовательно, они линейно независимы.
Отметим, что определитель Вронского в этом примере тождественно равен нулю. Однако, это не противоречит ни теореме 1, ни теореме 2, так как данные функции не образуют ФСР ни для какого линейного однородного дифференциального уравнения.
Задача 2. Найти общее решение уравнения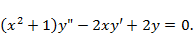 
Решение. Заметим, что данное уравнение имеет частное решение 
. Сделаем подстановку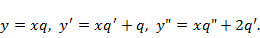 
Получим
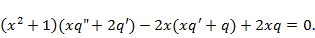
Замена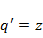 
приводит к линейному однородному уравнению 1-го порядка
Разделяя переменные и вычисляя интегралы, получим
Отсюда
Задача 3. Найти общие решения дифференциальных уравнений:
a1) 
Решение. Характеристическое уравнение 
имеет два действительных корня 
В соответствии с таблицей 1 (1-я строка) записываем общее решение 
.
a2) 
Решение. Как и в предыдущем примере, характеристическое уравнение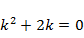 
имеет действительные корни 
Поскольку 
общее решение 
.
a3) 
Решение. Характеристическое уравнение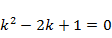 
имеет кратный действительный корень 
В соответствии с таблицей 1 (2-я строка) записываем общее решение 
.
a4) 
Решение. Характеристическое уравнение 
имеет отрицательный дискриминант 
Его корни – мнимые числа 
В соответствии с таблицей 1 (3-я строка, 
) записываем общее решение 
.
a5) 
Решение. Характеристическое уравнение 
имеет отрицательный дискриминант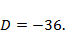 
Его комплексные корни 
В соответствии с таблицей 1 (3-я строка,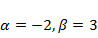 
) записываем общее решение 
.
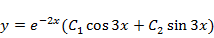Задача 4. В горизонтальном желобе находится идеальная пружина жесткости k. Левый конец пружины зафиксирован, а к правому – прикреплен груз массы m, который может перемещаться по желобу без трения. Пружину деформировали и отпустили. Найти период колебаний груза.
Решение. Пусть t – время, х – координата груза (х =0 соответствует недеформированной пружине). Согласно второму закону Ньютона и закону Гука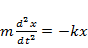 
. Чтобы решить полученное линейное ОДУ 2-го порядка с постоянными коэффициентами, составим характеристическое уравнение 
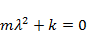. (Поскольку буква k обозначает один из параметров задачи, неизвестная обозначена буквой 
.) Найдем характеристические корни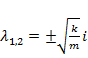 
. Отсюда получаем общее решение
При 
груз неподвижен. При любых других значениях констант груз колеблется с периодом 
.
Задача 5. Решить задачу Коши 
.
Решение. В примере а4) задачи 3 найдено общее решение данного ОДУ: . Отсюда дифференцированием находим 
. Подставляя в эти формулы начальные условия, находим значения констант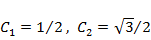 
. Таким образом, искомое частное решение
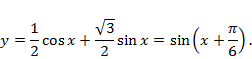
Задача 6. Обосновать правила нахождения ФСР для линейного однородного дифференциального уравнения 2-го порядка а) в случае вещественных различных корней; b) в случае кратного корня.
Решение. а) Будем искать частные решения, имеющие вид 
. Тогда 
. Подстановка этих выражений в ОДУ с постоянными коэффициентами и вынесение за скобки общего множителя 
приводит к уравнению
Таким образом, функция − частное решение ОДУ с постоянными коэффициентами тогда и только тогда, когда k – корень характеристического уравнения.
Осталось показать, что функции 
линейно независимы при 
. В самом деле, эти функции не пропорциональны, так как их отношение 
не является константой.
b) При наличии двукратного характеристического корня k ОДУ (7.3.1) обладает частным решением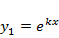 
. Это обосновано в предыдущем пункте. Следовательно, общее решение может быть найдено с помощью подстановки 
. При этом 
. Подставляя эти выражения в (7.3.1) и сокращая , получим
или, после перегруппировки членов
Два последних слагаемых равны нулю, поскольку k – кратный корень характеристического уравнения, а значит 
. Таким образом, q ”=0, откуда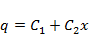 
. Наконец, 
.
Задача 7. Найти общие решения дифференциальных уравнений:
b1)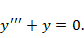 
Решение. Найдем корни характеристического уравнения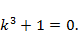 
ФСР состоит из функций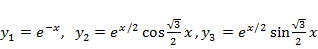 
. Общее решение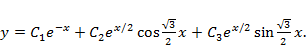 
b2)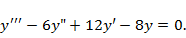 
Решение. Левая часть характеристического уравнения 
. Число 2 – действительный корень кратности 3. Общее решение
b3) 
Решение. Левая часть характеристического уравнения 
. Числа ± i – комплексные корни кратности 2. ФСР состоит из функций 
. Общее решение
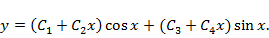
Задача 8. Решить уравнение Эйлера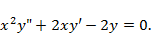 
Решение 1. Подставим функцию 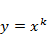и ее производные 
в исходное уравнение, получаем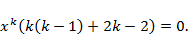 
Из алгебраического уравнения 
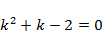находим корни 
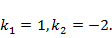Таким образом, ФСР состоит из функций 
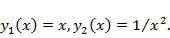Общее решение
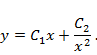
Решение 2. Сделаем замену независимой переменной 
Тогда
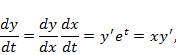
Исходное уравнение преобразуется в уравнение с постоянными коэффициентами
с общим решением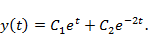 
Возвращаясь к исходной независимой переменной, получаем
