| §1 Выборка. Статистический ряд. Эмпирический закон распределения. Полигон и гистограмма | ||||||||||||||||||||||||||||||||||||||||||||||
Выборочной совокупностью(выборкой) называется совокупность случайно отобранных однородных объектов.
Генеральной совокупностью называется совокупность всех однородных объектов, из которых производится выборка.
Объемом совокупности (выборочной или генеральной) называется число объектов этой совокупности.
Способы отбора выборки:
1. Отбор, не требующий расчленения генеральной совокупности на части:
а) простой случайный бесповторный;
б) простой случайный повторный.
2. Отбор, при котором генеральная совокупность разбивается на части (если объем генеральной совокупности слишком большой):
а) типический отбор. Объекты отбираются не из всей генеральной совокупности, а из ее «типичных» частей. Например, цех из тридцати станков производит одну и ту же деталь. Тогда отбор делается по одной или по две детали с каждого станка в случайные моменты времени;
б) механический отбор. Например, если нужно выбрать 5% деталей, то выбирают не случайно, а каждую двадцатую деталь;
в) серийный отбор. Объекты выбирают не по одному, а сериями.
Итак, пусть из генеральной совокупности значений некоторого количественного признака произведена выборка объема N:
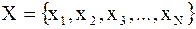 .
Таблица вида
Таблица 1 .
Таблица вида
Таблица 1
называется простым статистическим рядом, являющимся первичной формой представления статистического материала. Из данных таблицы 1 находят Размах выборки – это длина основного интервала Затем по формуле
где
Далее находятся частоты Результаты проведенных расчетов сводятся в таблицы: Таблица 2
Таблица 3
Далее находятся середины подынтервалов:
и после этого составляется еще одна таблица (таблица 4), которая называется статистическим рядом распределения. Статистический ряд распределения является оценкой теоретического ряда распределения и сходится к нему по вероятности. Поскольку ряд распределения является одной из форм задания закона распределения дискретной случайной величины, то мы получили эмпирический закон распределения исследуемой дискретной случайной величины. Таблица 4
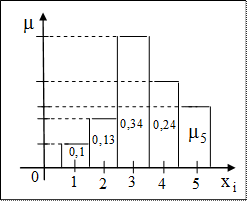
Гистограммой относительных частот называется ступенчатая фигура, состоящая из прямоугольников, основаниями которых служат частичные подынтервалы длины Для построения полигона относительных частот используются данные таблицы 4. В декартовой системе координат на оси Полигоном относительных частот называется ломаная, отрезки которой соединяют точки | Задача.
Из генеральной совокупности извлечена выборка объема n=70, полигон частот которой имеет вид
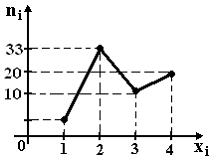 Тогда число вариант xi=1 в выборке равно…
Варианты ответов: 1) 8 2) 6 3) 7 4) 70
Решение.
По определению объем выборки есть сумма частот всех вариант выборки. Тогда n1+10+20+33=70, следовательно n1=7.
Ответ. №3.
Задача.
Выборка задана в виде гистограммы относительных частот. Найти относительную частоту
Тогда число вариант xi=1 в выборке равно…
Варианты ответов: 1) 8 2) 6 3) 7 4) 70
Решение.
По определению объем выборки есть сумма частот всех вариант выборки. Тогда n1+10+20+33=70, следовательно n1=7.
Ответ. №3.
Задача.
Выборка задана в виде гистограммы относительных частот. Найти относительную частоту 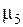 .
Варианты ответов: Ответы: 1). 0,19 2). 0,18
3). нет правильного ответа 4). 0,2 5). 0,17 .
Варианты ответов: Ответы: 1). 0,19 2). 0,18
3). нет правильного ответа 4). 0,2 5). 0,17
Решение. Как известно, площадь гистограммы относительных частот должна равняться 1. Поэтому Ответ. №1 | |||||||||||||||||||||||||||||||||||||||||||||
| §2 Статистические оценки генеральных параметров. Точечные и интервальные оценки для математического ожидания и дисперсии | ||||||||||||||||||||||||||||||||||||||||||||||
Пусть 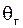 - некоторый параметр генеральной совокупности, который невозможно вычислить. Но знать его значение (хотя бы приближенное, оценочное) надо. Поэтому по выборочным данным производят расчет статистических оценок данного генерального параметра.
Оценки параметров подразделяются на точечные и интервальные.
Точечнойназывается статистическая оценка генерального параметра - некоторый параметр генеральной совокупности, который невозможно вычислить. Но знать его значение (хотя бы приближенное, оценочное) надо. Поэтому по выборочным данным производят расчет статистических оценок данного генерального параметра.
Оценки параметров подразделяются на точечные и интервальные.
Точечнойназывается статистическая оценка генерального параметра 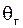 , определяемая одним числом. Интервальной называется статистическая оценка генерального параметра , определяемая одним числом. Интервальной называется статистическая оценка генерального параметра 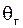 , которая определяется двумя числами , которая определяется двумя числами 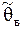 и и 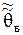 - концами интервала, покрывающего оцениваемый генеральный параметр - концами интервала, покрывающего оцениваемый генеральный параметр 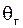 .
Несмещеннойназывают такую точечную оценку .
Несмещеннойназывают такую точечную оценку 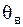 , математическое ожидание которой равно оцениваемому генеральному параметру при любом объеме выборки, то есть , математическое ожидание которой равно оцениваемому генеральному параметру при любом объеме выборки, то есть
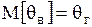 . (4)
Если равенство (4) нарушается, то в этом случае оценки . (4)
Если равенство (4) нарушается, то в этом случае оценки 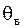 называется смещенной.
Эффективнойназывается точечная оценка называется смещенной.
Эффективнойназывается точечная оценка 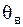 , которая (при заданном) объеме выборки) имеет наименьшую возможную дисперсию, то есть , которая (при заданном) объеме выборки) имеет наименьшую возможную дисперсию, то есть
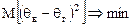 . (4а)
Состоятельной называется точечная оценка . (4а)
Состоятельной называется точечная оценка 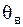 , которая (с увеличением объема выборки) стремится по вероятности к оцениваемому параметру , которая (с увеличением объема выборки) стремится по вероятности к оцениваемому параметру 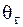 , то есть для любого достаточно малого , то есть для любого достаточно малого 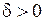
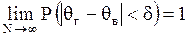 . (4б)
Несмещенной оценкой генеральной средней (генерального математического ожидания . (4б)
Несмещенной оценкой генеральной средней (генерального математического ожидания 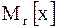 ) служит выборочная средняя (выборочное математическое ожидание): ) служит выборочная средняя (выборочное математическое ожидание):
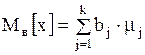 , (5)
где , (5)
где 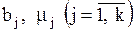 - варианты и их относительные частоты. Кроме того, - варианты и их относительные частоты. Кроме того, 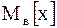 является состоятельной оценкой. Если случайная величина является состоятельной оценкой. Если случайная величина  подчинена нормальному закону распределения, то подчинена нормальному закону распределения, то 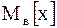 является и эффективной оценкой.
Смещенной оценкой генеральной дисперсии является и эффективной оценкой.
Смещенной оценкой генеральной дисперсии 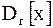 служит выборочная дисперсия: служит выборочная дисперсия:
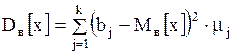 , (6)
где , (6)
где 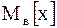 - рассчитывается по формуле (5), - рассчитывается по формуле (5), 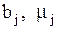 - данные из таблицы 4.
Иногда удобнее пользоваться другой формулой для вычисления выборочной дисперсии: - данные из таблицы 4.
Иногда удобнее пользоваться другой формулой для вычисления выборочной дисперсии:
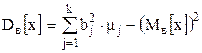 . (6a)
Замечание. Поскольку . (6a)
Замечание. Поскольку 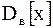 является смещенной оценкой, то ее «исправляют» следующим образом: является смещенной оценкой, то ее «исправляют» следующим образом:
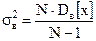 . (7)
Полученная оценка . (7)
Полученная оценка 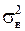 - это состоятельная несмещенная выборочная дисперсия, а - это состоятельная несмещенная выборочная дисперсия, а 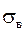 - выборочное среднее квадратичное отклонение.
При выборке малого объема - выборочное среднее квадратичное отклонение.
При выборке малого объема 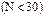 точечная оценка может значительно отличаться от оцениваемого генерального параметра, то есть приводит к грубым ошибкам. Поэтому при небольшом объеме выборки следует пользоваться интервальными оценками.
Пусть найденная (по данным выборки) статистическая оценка точечная оценка может значительно отличаться от оцениваемого генерального параметра, то есть приводит к грубым ошибкам. Поэтому при небольшом объеме выборки следует пользоваться интервальными оценками.
Пусть найденная (по данным выборки) статистическая оценка 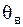 является оценкой неизвестного генерального параметра является оценкой неизвестного генерального параметра 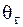 . Ясно, что . Ясно, что 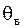 тем точнее определяет тем точнее определяет 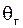 , чем меньше значение разности , чем меньше значение разности 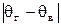 . То есть при . То есть при 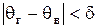 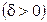 чем меньше чем меньше 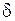 , тем оценка , тем оценка 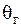 точнее. Значит, положительное число точнее. Значит, положительное число 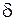 характеризует точность оценки.
Надежностью(доверительной вероятностью) оценки характеризует точность оценки.
Надежностью(доверительной вероятностью) оценки 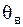 называется вероятность называется вероятность 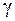 , с которой осуществляется событие , с которой осуществляется событие 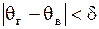 , то есть , то есть
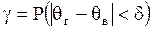 . (8)
Обычно надежность оценки (доверительная вероятность . (8)
Обычно надежность оценки (доверительная вероятность 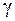 ) задается. Причем в качестве ) задается. Причем в качестве 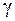 берут число, близкое к единице (0,95; 0,99; 0,999).
Доверительнымназывается интервал, который с заданной надежностью берут число, близкое к единице (0,95; 0,99; 0,999).
Доверительнымназывается интервал, который с заданной надежностью 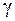 покрывает оцениваемый генеральный параметр. В соотношении (8), если раскрыть модуль, получается покрывает оцениваемый генеральный параметр. В соотношении (8), если раскрыть модуль, получается 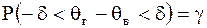 или или 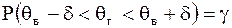 .
Тогда интервал .
Тогда интервал 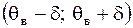 и есть доверительный интервал. Из общих соображений ясно, что длина доверительного интервала будет зависеть от объема выборки и есть доверительный интервал. Из общих соображений ясно, что длина доверительного интервала будет зависеть от объема выборки 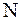 и доверительной вероятности и доверительной вероятности 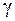 .
Для оценки математического ожидания .
Для оценки математического ожидания 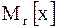 нормально распределенной генеральной совокупности нормально распределенной генеральной совокупности  по выборочной средней по выборочной средней 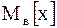 при известном среднем квадратическом отклонении при известном среднем квадратическом отклонении 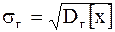 служит доверительный интервал: служит доверительный интервал:
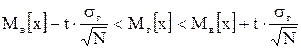 , (9)
где , (9)
где 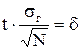 - точность оценки; - точность оценки; 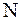 - объем выборки; - объем выборки; 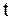 - такое значение аргумента функции Лапласа - такое значение аргумента функции Лапласа 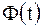 , при котором , при котором 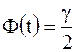 .
Для оценки математического ожидания .
Для оценки математического ожидания 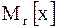 нормально распределенной генеральной совокупности нормально распределенной генеральной совокупности  по выборочной средней по выборочной средней 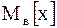 при неизвестном среднем квадратическом отклонении при неизвестном среднем квадратическом отклонении 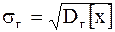 (при объеме выборки (при объеме выборки 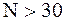 ) служит доверительный интервал: ) служит доверительный интервал:
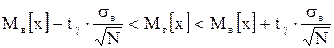 , (10)
где , (10)
где 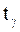 находим по таблице по заданным N и находим по таблице по заданным N и 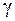 .
Для оценки среднего квадратического отклонения .
Для оценки среднего квадратического отклонения 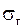 нормально распределенной генеральной совокупности нормально распределенной генеральной совокупности  с доверительной вероятностью с доверительной вероятностью 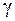 служат доверительные интервалы: служат доверительные интервалы:
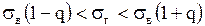 (при (при 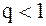 ); );
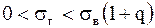 (при (при 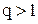 ), (11)
где q – находим по таблице при заданных N и ), (11)
где q – находим по таблице при заданных N и 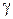 . .
|
Задача.
Точечная оценка математического ожидания нормального распределения равна 10. Тогда его интервальная оценка может иметь вид …
Варианты ответов: 1) (8, 5; 11,5) 2) (8,6; 9,6)
3) (10; 10,9) 4) (8,4; 10)
Решение.
Согласно определения, интервальная оценка есть интервал, содержащий оцениваемый параметр. Данному утверждению соответствует лишь ответ №1.
Ответ. №1.
Задача.
Дана выборка объема n. Если каждый элемент выборки увеличить в 5 раз, то выборочное среднее 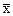 …
Варианты ответов: 1) увеличится в 25 раз 2) уменьшится в 5 раз
3) не изменится 4) увеличится в 5 раз
Решение.
Выборочная средняя: …
Варианты ответов: 1) увеличится в 25 раз 2) уменьшится в 5 раз
3) не изменится 4) увеличится в 5 раз
Решение.
Выборочная средняя:
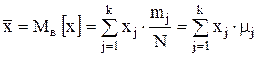 .
Поэтому, если каждый элемент выборки увеличить в 5 раз, то выборочное среднее .
Поэтому, если каждый элемент выборки увеличить в 5 раз, то выборочное среднее 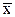
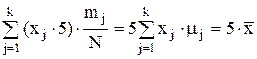 ,
т.е увеличится в 5 раз.
Ответ. №4.
Задача. Для выборки объема ,
т.е увеличится в 5 раз.
Ответ. №4.
Задача. Для выборки объема 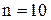 вычислена выборочная дисперсия вычислена выборочная дисперсия 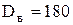 . Тогда исправленная дисперсия . Тогда исправленная дисперсия 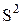 для этой выборки равна …
Варианты ответов: 1) 324 2) 200 3) 162 4) 400
Решение.
Поскольку для этой выборки равна …
Варианты ответов: 1) 324 2) 200 3) 162 4) 400
Решение.
Поскольку 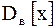 является смещенной оценкой, то ее «исправляют» следующим образом: является смещенной оценкой, то ее «исправляют» следующим образом: 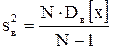 . Тогда . Тогда 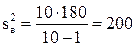 .
Ответ. №2.
Задача.
В результате измерений некоторой физической величины одним прибором (без систематических ошибок) получены следующие результаты (в мм): 11, 13, 15. тогда несмещенная оценка дисперсии измерений равна …
Варианты ответов: 1) 4 2) 3 3) 8 4) 0
Решение.
Несмещенной оценкой генеральной средней (математического ожидания .
Ответ. №2.
Задача.
В результате измерений некоторой физической величины одним прибором (без систематических ошибок) получены следующие результаты (в мм): 11, 13, 15. тогда несмещенная оценка дисперсии измерений равна …
Варианты ответов: 1) 4 2) 3 3) 8 4) 0
Решение.
Несмещенной оценкой генеральной средней (математического ожидания 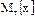 ) служит выборочная средняя: ) служит выборочная средняя:
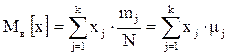 .
Смещенной оценкой генеральной дисперсии .
Смещенной оценкой генеральной дисперсии 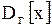 служит выборочная дисперсия: служит выборочная дисперсия:
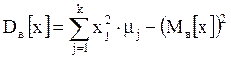 ,
Замечание. Поскольку ,
Замечание. Поскольку 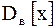 является смещенной оценкой, то ее «исправляют» следующим образом: является смещенной оценкой, то ее «исправляют» следующим образом:
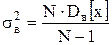 .
Полученная оценка .
Полученная оценка 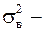 это несмещенная дисперсия, а это несмещенная дисперсия, а 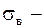 выборочное среднее квадратическое отклонение.
Таким образом, выборочное среднее квадратическое отклонение.
Таким образом,
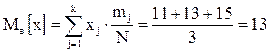 , ,
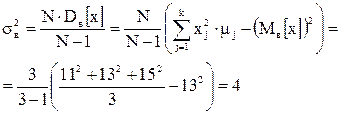 Ответ. №1.
Задача.
Мода вариационного ряда 1, 4, 4, 5, 6, 8, 9 равна...
Варианты ответов: 1) 5 2) 1 3) 9 4) 4
Решение.
По определению, мода есть варианта имеющая наибольшую частоту. В данном случае это есть варианта 4, т.к. она повторяется два раза, а все остальные - лишь по 1 разу.
Ответ. №4.
Ответ. №1.
Задача.
Мода вариационного ряда 1, 4, 4, 5, 6, 8, 9 равна...
Варианты ответов: 1) 5 2) 1 3) 9 4) 4
Решение.
По определению, мода есть варианта имеющая наибольшую частоту. В данном случае это есть варианта 4, т.к. она повторяется два раза, а все остальные - лишь по 1 разу.
Ответ. №4.
| |||||||||||||||||||||||||||||||||||||||||||||
| §3 Проверка статистической гипотезы о законе распределения генеральной совокупности | ||||||||||||||||||||||||||||||||||||||||||||||
Статистической гипотезой 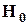 называется любое предположение относительно закона распределения исследуемой случайной величины называется любое предположение относительно закона распределения исследуемой случайной величины  .
Гипотезы бывают простые и сложные. Простая гипотеза полностью определяет закон распределения величины .
Гипотезы бывают простые и сложные. Простая гипотеза полностью определяет закон распределения величины  в отличие от сложной.
Гипотезы бывают параметрическими и непараметрическими. В первом случае мы имеем предположение о параметрах распределения при известном законе, а во втором – о самом виде закона распределения.
Наряду с выдвинутой гипотезой в отличие от сложной.
Гипотезы бывают параметрическими и непараметрическими. В первом случае мы имеем предположение о параметрах распределения при известном законе, а во втором – о самом виде закона распределения.
Наряду с выдвинутой гипотезой 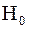 рассматривают противоречащую ей гипотезу рассматривают противоречащую ей гипотезу 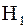 . Если выдвинутая гипотеза . Если выдвинутая гипотеза 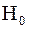 будет отвергнута, то имеет место противоречащая ей гипотеза будет отвергнута, то имеет место противоречащая ей гипотеза 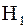 .
Критерием проверки статистической гипотезы называется некоторое правило, позволяющее принять ее или отвергнуть. Причем критерии строятся с помощью случайной величины .
Критерием проверки статистической гипотезы называется некоторое правило, позволяющее принять ее или отвергнуть. Причем критерии строятся с помощью случайной величины 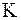 (часто именно ее называют критерием), для которой известно распределение. Наблюдаемым значением критерия (часто именно ее называют критерием), для которой известно распределение. Наблюдаемым значением критерия 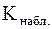 называют значение критерия, вычисленное по данным выборки.
В случае проверки гипотез возможны ошибки:
Ошибка 1-го рода состоит в том, что будет отвергнута правильная гипотеза. Вероятность ошибки первого рода называют значение критерия, вычисленное по данным выборки.
В случае проверки гипотез возможны ошибки:
Ошибка 1-го рода состоит в том, что будет отвергнута правильная гипотеза. Вероятность ошибки первого рода 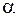 называется уровнем значимости критерия, по которому производится проверка.
Ошибка 2-го рода состоит в том, что будет принята неправильная гипотеза. Если называется уровнем значимости критерия, по которому производится проверка.
Ошибка 2-го рода состоит в том, что будет принята неправильная гипотеза. Если 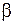 - вероятность ошибки второго рода, то величина - вероятность ошибки второго рода, то величина 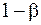 называется мощностью критерия.
Параметрические гипотезы проверяются с помощью критериев значимости, а непараметрические – с помощью критериев согласия.
Критическойобластью называется совокупность значений критерия, при которых нулевую гипотезу отвергают. Если уровень значимости называется мощностью критерия.
Параметрические гипотезы проверяются с помощью критериев значимости, а непараметрические – с помощью критериев согласия.
Критическойобластью называется совокупность значений критерия, при которых нулевую гипотезу отвергают. Если уровень значимости 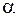 уже выбран и задан объем выборки, то критическую область следует строить так, чтобы мощность критерия была максимальной. Выполнение этого требования должно обеспечить минимальную ошибку второго рода, что более желательно.
Основной принцип проверки статистических гипотез: если уже выбран и задан объем выборки, то критическую область следует строить так, чтобы мощность критерия была максимальной. Выполнение этого требования должно обеспечить минимальную ошибку второго рода, что более желательно.
Основной принцип проверки статистических гипотез: если 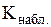 принадлежит критической области – гипотезу принадлежит критической области – гипотезу 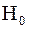 отвергают, если же отвергают, если же 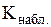 принадлежит области принятия гипотезы, то гипотезу принадлежит области принятия гипотезы, то гипотезу 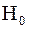 принимают. принимают.
| Пример 1. Гипотеза 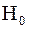 о том, что математическое ожидание нормальной величины равно о том, что математическое ожидание нормальной величины равно 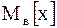 при условии, что дисперсия при условии, что дисперсия 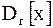 известна, является простой параметрической. Если же дисперсия известна, является простой параметрической. Если же дисперсия 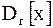 неизвестна, то гипотеза будет сложной параметрической.
Пример 2. Гипотеза неизвестна, то гипотеза будет сложной параметрической.
Пример 2. Гипотеза 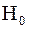 о том, что случайная величина распределена по нормальному (или по какому-то другому) закону, является сложной непараметрической.
Задача.
Если основная гипотеза имеет вид H0: a=20, то конкурирующей может быть гипотеза …
Варианты ответов: 1) H1: a³20 2) H1: a³10
3) H1: a>20 4) H1: a£20
Решение.
Конкурирующая гипотеза должна противоречитьвыдвинутой, поэтому верный ответ №3.
Ответ. №3. о том, что случайная величина распределена по нормальному (или по какому-то другому) закону, является сложной непараметрической.
Задача.
Если основная гипотеза имеет вид H0: a=20, то конкурирующей может быть гипотеза …
Варианты ответов: 1) H1: a³20 2) H1: a³10
3) H1: a>20 4) H1: a£20
Решение.
Конкурирующая гипотеза должна противоречитьвыдвинутой, поэтому верный ответ №3.
Ответ. №3.
| |||||||||||||||||||||||||||||||||||||||||||||
| §4 Статистическая и корреляционная зависимости. Эмпирическая и теоретическая линии регрессии | ||||||||||||||||||||||||||||||||||||||||||||||
Две случайные величины могут быть связаны между собой функциональной зависимостью, либо зависимостью другого рода, называемой статистической, либо быть независимыми.
Статистическойназывают зависимость, при которой изменение одной из величин влечет изменение распределения другой. Если при изменении одной из величин изменяется среднее значение другой, то в этом случае статистическую зависимость называют корреляционной.Значит, корреляционная зависимость есть частный случай статистической зависимости.
Корреляционной зависимостью 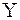 от от  называют функциональную зависимость условной средней называют функциональную зависимость условной средней 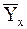 от от  : :
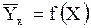 . (12)
Уравнение (1) называется уравнением регрессии . (12)
Уравнение (1) называется уравнением регрессии 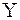 на на  ; функция ; функция 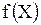 называется регрессией называется регрессией 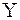 на на  ; график функции ; график функции 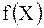 - линией регрессии - линией регрессии 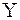 на на  .
Корреляционной зависимостью .
Корреляционной зависимостью  от от 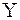 называется функциональная зависимость называется функциональная зависимость 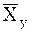 от от 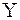 : :
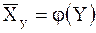 . (13)
Уравнение (13) называется уравнением регрессии . (13)
Уравнение (13) называется уравнением регрессии  на на 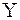 ; функция ; функция 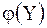 называется регрессией называется регрессией  на на 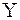 ; график функции ; график функции 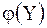 - линией регрессии - линией регрессии  на на 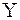 .
Наиболее простой и важный случай корреляционной зависимости - линейная регрессия. В этом случае теоретическое уравнение линейной регрессии .
Наиболее простой и важный случай корреляционной зависимости - линейная регрессия. В этом случае теоретическое уравнение линейной регрессии 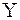 на на  (формула (12) имеет вид (формула (12) имеет вид
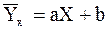 . (14)
Коэффициент . (14)
Коэффициент 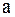 в уравнении (14) называют коэффициентом регрессии в уравнении (14) называют коэффициентом регрессии 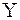 на на  и обозначают и обозначают 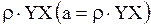 .
Уравнение линейной регрессии .
Уравнение линейной регрессии  на на 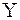 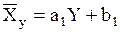 . (15)
Коэффициент . (15)
Коэффициент 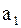 называют коэффициентом регрессии называют коэффициентом регрессии  на на 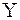 и обозначают и обозначают 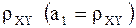 .
В случае линейной регрессии задача определения тесноты связи сводится к вычислению эмпирического (выборочного) коэффициента корреляции, который можно вычислить по одной из формул: .
В случае линейной регрессии задача определения тесноты связи сводится к вычислению эмпирического (выборочного) коэффициента корреляции, который можно вычислить по одной из формул:
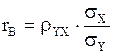 или или 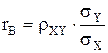 , (16)
где , (16)
где 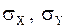 - значения средних квадратических отклонений.
Свойства выборочного коэффициента корреляции
1. - значения средних квадратических отклонений.
Свойства выборочного коэффициента корреляции
1. 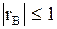 или или 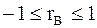 .
2. Если .
2. Если 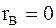 , тогда , тогда  и и 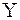 не связаны линейной корреляционной зависимостью (но могут быть связаны нелинейной корреляционной или даже функциональной зависимостью).
3. С возрастанием абсолютной величины выборочного коэффициента корреляции линейная корреляционная зависимость становится более тесной и при не связаны линейной корреляционной зависимостью (но могут быть связаны нелинейной корреляционной или даже функциональной зависимостью).
3. С возрастанием абсолютной величины выборочного коэффициента корреляции линейная корреляционная зависимость становится более тесной и при 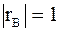 переходит в линейную функциональную зависимость.
4. Если переходит в линейную функциональную зависимость.
4. Если 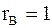 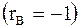 , тогда , тогда  и и 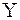 связаны прямой (обратной) линейной функциональной зависимостью. связаны прямой (обратной) линейной функциональной зависимостью.
|
Задача.
Выборочное уравнение парной регрессии имеет вид 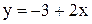 . Тогда выборочный коэффициент корреляции может быть равен …
Варианты ответов: 1) 0,6 2) -0,6 3) -3 4) -2
Решение.
По свойству 1, оставляем как возможные, ответы № 1, 2. Т.к. по условию уравнение парной регрессии имеет вид . Тогда выборочный коэффициент корреляции может быть равен …
Варианты ответов: 1) 0,6 2) -0,6 3) -3 4) -2
Решение.
По свойству 1, оставляем как возможные, ответы № 1, 2. Т.к. по условию уравнение парной регрессии имеет вид 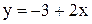 , т.е. с ростом x возрастает в среднем и y, то rB>0, т.е. выбираем ответ № 1.
Ответ. №1. , т.е. с ростом x возрастает в среднем и y, то rB>0, т.е. выбираем ответ № 1.
Ответ. №1.
|
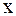
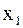
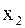
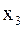
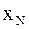
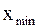 и
и 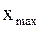 , соответственно наименьшее и наибольшее значения выборки. Затем данные таблицы 1 называемые вариантами, располагают в порядке возрастания. Тогда выборка
, соответственно наименьшее и наибольшее значения выборки. Затем данные таблицы 1 называемые вариантами, располагают в порядке возрастания. Тогда выборка 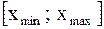 , в который попадают все значения выборки. Вычисляется размах выборки следующим образом:
, в который попадают все значения выборки. Вычисляется размах выборки следующим образом: 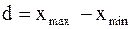 .
.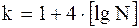 , (1)
, (1)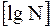 - целая часть числа
- целая часть числа 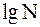 , определяется число
, определяется число 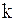 . Данное число задает количество подынтервалов (классов), на которые разбиваем основной интервал. Длины h подынтервалов и их границы
. Данное число задает количество подынтервалов (классов), на которые разбиваем основной интервал. Длины h подынтервалов и их границы 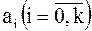 вычисляются по формулам
вычисляются по формулам 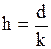 , (2)
, (2)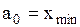 ;
; 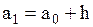 ; …;
; …; 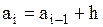 ; …;
; …; 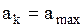 . (3)
. (3)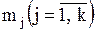 и относительные частоты
и относительные частоты 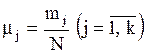 попадания значений выборки
попадания значений выборки 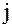 -й подынтервал. Причем для частот должно выполняться равенство
-й подынтервал. Причем для частот должно выполняться равенство 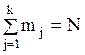 , а для относительных частот соответственно
, а для относительных частот соответственно 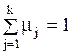 .
.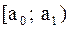
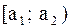
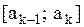
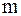
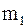
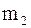
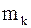
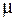
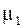
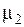

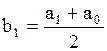 ;
; 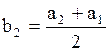 ; …;
; …; 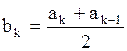
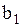
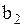
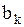
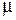
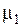
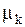
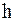 , а высоты равны числам
, а высоты равны числам 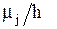 (плотности вероятностей)
(плотности вероятностей) 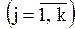 . Аналогичным образом, по данным таблицы 2 строится гистограмма частот.
. Аналогичным образом, по данным таблицы 2 строится гистограмма частот. находятся
находятся 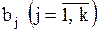 . По оси
. По оси  откладываются значения, соответствующие относительным частотам
откладываются значения, соответствующие относительным частотам 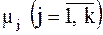 .
.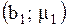 ;
; 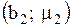 ; …;
; …; 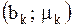 . Полигон относительных частот есть визуальное представление эмпирического закона распределения выборки.
. Полигон относительных частот есть визуальное представление эмпирического закона распределения выборки.