Лабораторная работа №4. Метод наименьших квадратов

По мере того как проведен анализ данных первичными методами обработки данных, приступают к вторичным методам статистической обработки данных, на основании которых определяются статистические закономерности в имеющемся наборе данных. В частности, может возникнуть ситуация, когда нам необходимо описать, имеющуюся выборку, некоторой аппроксимирующей функцией (например, с целью прогноза развития событий или для получения значений функции при различных вариациях аргумента). Одним из наиболее популярных методов решения подобных задач является метод наименьших квадратов (МНК).

Рассмотрим решение задачи в графической интерпретации. Допустим имеется некоторая выборка наблюдений за поведением объекта, объемом в 11 наблюдений, где в зависимости от параметра x изменяется результат y (табл. 4.1).

Табл. 4.1. Выборка наблюдений

Требуется найти эмпирическую формулу 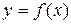, отражающую зависимость y от x, где - аппроксимирующая функция.

В том случае, когда мы имеем зависимости функции от одной и двух переменных, возможно построение точечной диаграммы на основании имеющейся выборки с целью формирования гипотезы о виде аппроксимирующей функции. На рис. 4.1 представлена точечная диаграмма, отражающая зависимость представленную в табл. 4.1.

Рис. 4.1. Точечная диаграмма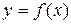

Найденная эмпирическая формула 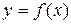должна отражать для выборки (табл. 4.1) линию, проведенную таким образом, что суммарное квадратичное отклонение линии от каждой заданной точки выборки стремилось к нулю (рис. 4.2). Вид линии зависит от расположения точек выборки на графике. В каждой точке отклонение может иметь либо положительное, либо отрицательное значение. Именно по этой причине по каждой точке берется квадрат отклонения, чтобы избежать ситуации, в которой при суммировании отклонения ошибки компенсировали друг друга.

Рис. 4.2. – График функции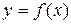

Рассмотрим механизм МНК в общем виде. По экспериментальным данным строится точечный график, на основании распределения точек на координатной плоскости выдвигается гипотеза относительно вида аппроксимирующей функции. В качестве могут выступать функции, представленные в табл. 4.2.

Табл. 4.2. Аппроксимирующие функции

Наименование функции	Математическое представление функции
Линейная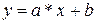
Гипербола
Степенная
Показательная
Логарифмическая
Дробно-линейная
Дробно-рациональная
Параболическая

При наличии опыта исследователь может выбрать наиболее подходящий вид аппроксимирующей функции. В противном случае ведется поиск коэффициентов по всем доступным видам аппроксимирующих функций, а выбор осуществляется по критерию среднеквадратического отклонения. После выбора вида аппроксимирующей функции необходимо подобрать параметры таким образом, чтобы суммарное квадратное отклонение для всех наблюдений в выборке (табл. 4.1) стремилось к нулю. Необходимо оценить каждый вид и выбрать наиболее подходящую по параметру среднеквадратического отклонения.

Отклонение каждого измеренного значения от вычисленного по аппроксимирующей функции определяется по формуле (1).

(1)

где - i -е значение функции от аргумента (берется из имеющейся выборки наблюдений);

- значение аппроксимирующей функции в точке .

Далее по формуле (2) рассчитывается суммарное отклонение (функция потерь, функция риска) 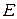для всех точек выборки.

(2)

где - число элементов в исходной выборке.

Подставив в (2) выражение (1) получим выражение для определения меры отклонения (3) в общем виде.

(3)

Таким образом, критерий эффективности аппроксимирующей функции заключается в подборе параметров таким образом, чтобы величина 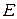была наименьшей (4).

(4)

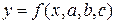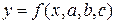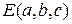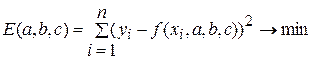Следовательно, суть МНК сводится к поиску экстремума функции (минимума) (4). Рассмотрим решение задачи на примере аппроксимирующей функции с тремя параметрами . Подставим в выражение (4) и получим суммарное отклонение зависящее от трех параметров (5).

(5)

С целью поиска минимума функции (5) используется необходимое условие экстремума функции нескольких переменных (6).

(6)

Таким образом, с учетом (6) задача минимизации сводится к решению системы уравнений (7), полученных вычислением частных производных от функции (для определения частных производных необходимо воспользоваться следующим выражением: .

(7)

Выводим в системе уравнений (7) константу 2 за сумму и делим правую и левую части равенств на 2. В результате получаем систему (8).

(8)

Решив систему уравнений (8) любым способом (метод подстановки, метод Гаусса, метод Жордана – Гаусса, метод обратной матрицы, метод Зейделя) определяют параметры аппроксимирующей функции .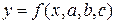

Далее осуществляется оценка точности аппроксимирующей функции (9).

(9)

Сведя всю информацию воедино можно сформулировать алгоритм МНК, который сводится к выполнению следующих действий:

1. Графическое построение (точечная диаграмма) имеющейся выборки наблюдений;

2. Подбор наиболее подходящего эмпирического выражения 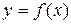или группы выражений, отражающих данные на графике.

3. Записать формулу суммарного отклонения (5).

4. Составить систему уравнений по формуле (6).

5. Решить полученную систему уравнений (8) доступным методом.

6. Оценивается точность аппроксимации параметром среднеквадратического отклонения по формуле (9) и выбирается наилучшая аппроксимация.

В некоторых случаях переходят от нелинейных зависимостей к квазилинейным (линейные зависимости, полученные из нелинейных посредством преобразований) вида , где 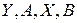- преобразованные значения (табл. 4.4).

Табл. 4.4. Квазилинейные функции

Наименование функции	Математическое представление функции	Преобразование переменных	Квазилинейное представление
Гипербола
Степенная		При
Показательная		При
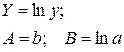
Логарифмическая
Дробно-линейная
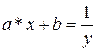
Дробно-рациональная

Таким образом, строятся квазилинейные аппроксимирующие функции вида . С учетом введенных обозначений параметры , преобразованные в , подставляются в исходное уравнение .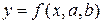

В том случае, если двухпараметрическая зависимость не приводит к желаемому результату, то поиск продолжается среди формул с большим количеством параметров.

Пример. Рассмотрим поиск параметров в общем виде для параболической зависимости . В данном случае пропускаются шаги 1 и 2 алгоритма поиска МНК.

3.

4.

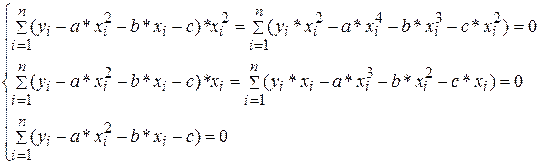
После преобразований получается следующая система уравнений:

5. Для решения полученной системы уравнений можно воспользоваться вспомогательной таблицей (табл. 4.3).

Табл. 4.3. Вспомогательная таблица

…………………….
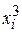
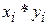
n

Далее решается система уравнений, например, методом подстановок, в результате чего определяются коэффициенты .

6. Оценивается точность аппроксимации параметром среднеквадратического отклонения по формуле (9).