Входная информация.
Приступая к изучению данной темы, Вам необходимо восстановить в памяти (или восполнить) знания:
- из предыдущих разделов:числовая последовательность и ее предел. Основные теоремы о пределах (ПМ - МА.3); методика нахождения предела числовой последовательности (ПМ - МА. 4).
Содержание темы
Структурно-логическая схема содержания темы
5.2.2. Тематическое содержание.
Предел функции.
Изучая предел последовательности, мы рассматривали функцию целочисленного аргумента. Теперь мы рассмотрим функцию у = f (х) непрерывного аргумента х, областью ее определения служит один или несколько интервалов (конечных или бесконечных) числовой оси. Введем важнейшее в математике понятие предела функции. Это понятие играет фундаментальную роль во всем математическом анализе.
Пусть независимая переменная х неограниченно приближается к числу х 0. Это означает, что мы придаем х значения сколь угодно приближающиеся к х 0, но не равные х 0. Запишем это так: х ® х 0 и будем говорить, что х стремится к х 0. Может оказаться при этом, что соответствующие значения f (х) неограниченно приближаются к некоторому числу А. Тогда говорят, что число А есть предел функции у = f (х) при х ® х 0 или что функция у = f (х) стремится к числу А при х ® х 0.
Определение предела функции в точке «на языке последовательностей» (5.1).
Число А называется пределом функции у = f (х) при х стремящемся к х 0, если для любой последовательности точек х, достаточно мало отличающихся от х 0, последовательность соответствующих значений функции f (х) как угодно мало отличаются от числа А.
| 5.1. Определение предела функции в точке «на языке последовательностей» (адрес файла Блок 4 ____). Число А называется пределом функции у = f (х) при х стремящемся к х 0, если для любой последовательности точек х, достаточно мало отличающихся от х 0, последовательность соответствующих значений функции f (х) как угодно мало отличаются от числа А. Вернитесь к тексту |
Если А есть предел функции f (х) при х ® х 0, то это записывают так:
.
Предельная точка (5.2).
Точка х 0, к которой стремится независимая переменная х, называется ее предельной точкой.
| 5.2. Предельная точка (адрес файла Блок 4 ___). Точка х 0, к которой стремится независимая переменная х, называется ее предельной точкой. Вернитесь к тексту |
Следует обратить внимание на тот факт, что в определении предела функции не требуется, чтобы функция была задана и в предельной точке; нужно только, чтобы функция была определена в какой-нибудь окрестности предельной точки, но не обязательно в самой точке. Например, функция
не определена при х = 0, но, как это будет доказано, она стремится к 1 при х, стремящемся к нулю. Отыскание предела функции, определенной в некоторой окрестности точки х 0, но не в ней самой, и будет составлять одну из важнейших задач теории пределов.
Определение предела функции в точке «на языке e - d » (5.3).
Число А называется пределом функции f (х) в точке х 0, если для любого сколь угодно малого числа e > 0 найдется такое число d > 0, что для всех х ¹ х 0, удовлетворяющих неравенству ½ х – х 0½ < d, выполняется неравенство ½ f (х) – А ½ < e.
| 5.3. Определение предела функции в точке «на языке e - d » (адрес файла Блок 4 ___). Число А называется пределом функции f (х) в точке х 0, если для любого сколь угодно малого числа e > 0 найдется такое число d > 0, что для всех х ¹ х 0, удовлетворяющих неравенству ½ х – х 0½ < d, выполняется неравенство ½ f (х) – А ½ < e. Вернитесь к тексту |
Наличие у функции у = f (х) при х ® х 0 предела равного А, геометрически иллюстрируется следующим образом: восстанавливаем к оси Ох в точке х 0 и к оси Оу в точке А перпендикуляры, продолжив их до пересечения в точке М, и произвольно зададим положительное число e; тогда найдется такая d - окрестность точки х = х 0, что часть графика функции у = f (х), соответствующая этой окрестности, будет содержаться в полосе, ограниченной прямыми
у = А - e и у = А + e.
Чтобы проверить вычислениями, что число А есть предел функции f (х) при х ® х 0, поступают так: задают положительное как угодно малое число e. Если для него можно найти такое положительное число d, что для всех х (не равных х 0), удовлетворяющих неравенству ½ х - х 0½ < d (т.е. для х, принадлежащих d - окрестности точки х 0), будет справедливо также и неравенство ½ f (х) - А ½ < e, то число А действительно есть предел функции f (х) при х ® х 0.
В качестве примере возьмем функцию у = 2 х + 1 и докажем, что она имеет предел при х ®1, равный 3. Зададим положительное число e. Для того чтобы имело место неравенство
½(2 х + 1) - 3½ < e или, что то же, неравенство 2 ½ х - 1½ < e нужно, чтобы было выполнено неравенство
.
Таким образом, для всех х, отличающихся от 1 меньше, чем на e /2, наша функция будет отличаться от 3 меньше, чем на e, где e - произвольное положительное число, и, следовательно, функция у = 2 х + 1 в самом деле стремится к 3 при х ®1. В этом примере можно взять
.
Следует обратить внимание, что d зависит от e, d = d (e), чем больше e, тем d, вообще говоря, больше.
Бесконечно большой аргумент.
Пусть независимая переменная х функции у = f (х) неограниченно возрастает. Это означает, что мы придаем х любое значение, большее всякого наперед заданного положительного числа. В этом случае говорят, что х стремится к положительной бесконечности, и записывают так х ® +¥. Если х неограниченно убывает, то есть становится меньше всякого наперед заданного отрицательного числа, то говорят, что х стремится к отрицательной бесконечности, и записывают так: х ® -¥.
Бесконечно большой аргумент (5.4).
Если независимая переменная х функции у = f (х) стремится к ±¥, то такой аргумент называется бесконечно большим.
| 5.4. Бесконечно большой аргумент (адрес файла Блок 4 ____). Если независимая переменная х функции у = f (х) стремится к ±¥, то такой аргумент называется бесконечно большим. Вернитесь к тексту |
Изучая функцию f (х) при бесконечно большом аргументе, мы предполагаем, что она определена при всех рассматриваемых значениях х.
Определение предела функции при х ® +¥ «на языке последовательностей» (5.5).
Число А называется пределом функции f (х) при х ® +¥, если для любой бесконечно большой последовательности значений аргумента соответствующая последовательность значений функции сходится к А.
| 5.5. Определение предела функции при х ® +¥ «на языке последовательностей» (адрес файла Блок 4 ____). Число А называется пределом функции f (х) при х ® +¥, если для любой бесконечно большой последовательности значений аргумента соответствующая последовательность значений функции сходится к А. Вернитесь к тексту |
Если А есть предел функции f (х) при х ® +¥, то это записывают так
.
Определение предела функции при х ® +¥ «на языке e - d » (5.6).
Число А называется пределом функции f (х) при х ® +¥, если для любого e > 0 найдется такое вещественное число N, что ½ f (х) - А ½ < e для всех значений х > N.
| 5.6. Определение предела функции при х ® +¥ «на языке e - d » (адрес файла Блок 4 ____). Число А называется пределом функции f (х) при х ® +¥, если для любого e > 0 найдется такое вещественное число N, что ½ f (х) - А ½ < e для всех значений х > N. Вернитесь к тексту |
Наличие у функции у = f (х) при х ® +¥ предела равного А, геометрически иллюстрируется следующим образом: восстановим к оси Оу в точке А перпендикуляр и произвольно зададим положительное число e. Тогда найдется такое число N, что часть графика функции у = f (х), соответствующая значениям х, большим этого числа, будет содержаться в полосе, ограниченной прямыми у = А - e и у = А + e.
Определение и геометрический смысл предела функции при х ® -¥ совершенно аналогичны только что рассмотренным.
Если неравенство ½ f (х) - А ½ < e выполняется для всех х, удовлетворяющих условию
½ х ½ > N, то это будет означать, что х может стремится к бесконечности произвольным образом, т.е. А является пределом функции и при х ® +¥ и при х ® -¥, т.е. х ® ¥.
В разделе ВМ. МА – 3 было введено понятие бесконечно большой последовательности и бесконечно малой последовательности. Сейчас мы введем понятие бесконечно большой величины и бесконечно малой.
Определение бесконечно большой величины «на языке последовательностей» (5.7).
Если для любой последовательности х, сходящейся к х 0, соответствующая последовательность значений функции по абсолютной величине превосходит любое наперед заданное сколь угодно большое положительное число, то функция f (х) называется бесконечно большой.
| 5.7. Определение бесконечно большой величины «на языке последовательностей» (адрес файла Блок 4 ____). Если для любой последовательности х, сходящейся к х 0, соответствующая последовательность значений функции по абсолютной величине превосходит любое наперед заданное сколь угодно большое положительное число, то функция f (х) называется бесконечно большой. Вернитесь к тексту |
Записывают это так 
.
Функция у = f (х), являющаяся при х ® х 0 бесконечно большой величиной, не имеет предела в обычном смысле. Говорят, что функция f (х) стремится к бесконечности или имеет своим пределом бесконечность. Если функция стремится к отрицательной бесконечности, то это записывают так: 
, если к положительной – 
.
Другое определение бесконечно большой величины (5.8).
Функция f (х) называется бесконечно большой величиной при х ® х 0, если для любого как угодно большого положительного числа М, можно подобрать такое положительное d, что для всех х, удовлетворяющих неравенству ½ х - х 0½ < d,будет справедливо неравенство ½ f (х) ½ < М.
| 5.8. Другое определение бесконечно большой величины (адрес файла Блок 4 ___). Функция f (х) называется бесконечно большой величиной при х ® х 0, если для любого как угодно большого положительного числа М, можно подобрать такое положительное d, что для всех х, удовлетворяющих неравенству ½ х - х 0½ < d,будет справедливо неравенство ½ f (х) ½ < М. Вернитесь к тексту |
Следует заметить, что нельзя смешивать постоянное очень большое число с бесконечно большой величиной.
Тот факт, что функция у = f (х) при х ® х 0 является бесконечно большой величиной, геометрически иллюстрируется следующим образом: произвольно зададим положительное число М. Тогда найдется такая d - окрестность точки х 0, что часть графика функции у = f (х), соответствующая этой d - окрестности, будет находится вне полосы, ограниченной прямыми у = М и у = - М.
Определение бесконечно малой величины (5.9).
Если для любой последовательности х, сходящейся к х 0, соответствующая последовательность значений функции сходится к нулю, то функция называется бесконечно малой.
| 5.9. Определение бесконечно малой величины (адрес файла Блок 4 ___). Если для любой последовательности х, сходящейся к х 0, соответствующая последовательность значений функции сходится к нулю, то функция называется бесконечно малой. Вернитесь к тексту |
Определение бесконечно малой величины «на языке e - d » (5.10).
Функция f (х) называется бесконечно малой при х ® х 0, если для любого e > 0 найдется такое d > 0, что из выполнения неравенства ½ х - х 0½ < d, следует неравенство ½ f (х) ½ < e.
| 5.10. Определение бесконечно малой величины «на языке e - d » (адрес файла Блок 4 ___). Функция f (х) называется бесконечно малой при х ® х 0, если для любого e > 0 найдется такое d > 0, что из выполнения неравенства ½ х - х 0½ < d, следует неравенство ½ f (х) ½ < e. Вернитесь к тексту |
Нельзя смешивать постоянное очень малое число с бесконечно малой величиной. Только нуль является числом, которое можно рассматривать в качестве бесконечно малой.
Определение ограниченной функции в данном интервале (5.11).
Функция у = f (х) называется ограниченной в данном интервале, если существует такое положительное число М, что при всех значениях х, принадлежащих этому интервалу, выполняется соотношение ½ f (х) ½ £ М. В противном случае функция называется неограниченной.
| 5.11. Определение ограниченной функции в данном интервале (адрес файла Блок 4 ____). Функция у = f (х) называется ограниченной в данном интервале, если существует такое положительное число М, что при всех значениях х, принадлежащих этому интервалу, выполняется соотношение ½ f (х) ½ £ М. В противном случае функция называется неограниченной. Вернитесь к тексту |
Определение ограниченной функции при х ® х 0 (5.12).
Функция называется ограниченной при х ® х 0, если в некоторой окрестности точки х 0 эта функция ограничена.
| 5.12 Определение ограниченной функции при х ® х 0 (адрес файла Блок 4 ____). Функция называется ограниченной при х ® х 0, если в некоторой окрестности точки х 0 эта функция ограничена. Вернитесь к тексту |
Кроме рассмотренного нами понятия предела функции в точке, существуют также понятия предела в точке слева и справа.
Если в определении предела функции потребовать, чтобы х стремилось к х 0 не любым способом, а только слева (оставаясь все время меньше х 0), то получим определение предела слева в точке х 0. Аналогично, если существует предел функции f (х) в точке х 0 при условии, что х стремится к х 0 только справа (оставаясь все время больше х 0), то такой предел называется пределом справа. Пределы слева и справа иначе называются односторонними пределами и соответственно обозначаются так:
, 
.
Из определения предела следует, что если функция имеет в какой-либо внутренней точке промежутка предел, то она имеет в этой точке и односторонние пределы, причем
.
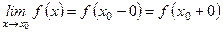Связь между бесконечно малой величиной и бесконечно большой была рассмотрена в ВМ. МА – 3 (п. 3.8).
Здесь мы только сформулируем теорему, не повторяя доказательства, которое аналогично упомянутому.
Теорема. Если функция f (х) – бесконечно большая величина, то 
- бесконечно малая величина; если j (х) – бесконечно малая величина, то 
- бесконечно большая величина.
Теорема о функции, имеющей предел (5.13).
Если функция имеет предел, то ее можно представить как сумму постоянной, равной ее пределу, и бесконечно малой величины.
| 5.13. Теорема о функции, имеющей предел (адрес файла Блок 4 ___). Если функция имеет предел, то ее можно представить как сумму постоянной, равной ее пределу, и бесконечно малой величины. Вернитесь к тексту |
Доказательство. Пусть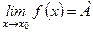 
. Тогда, если e - произвольное малое положительное число, то ½ f (х) - А ½ < e для всех х, достаточно близких к х 0, а это означает, в соответствии с определением, что f (х) - А есть бесконечно малая величина. Следовательно,
f (х) - А = a (х), или f (х) = А + a (х), где a (х) – бесконечно малая величина при х ® х 0.
Справедлива и обратная теорема: Если функцию можно представить как сумму постоянной и бесконечно малой величины, то постоянное слагаемое есть предел функции.
Напомним теоремы о бесконечно малых, доказательство которых дано в ВМ. МА – 3 (п. 3.9).
Теорема 1. Сумма конечного числа бесконечно малых величин есть бесконечно малая величина.
Теорема 2. Произведение ограниченной функции на бесконечно малую есть бесконечно малая величина.
Применяя эти теоремы, можно сформулировать следующие теоремы о пределах:
Теоремы о пределах.
Теоремы о пределах (5.14).
Теорема 1. Предел суммы конечного числа слагаемых равен сумме пределов этих слагаемых.
Теорема 2. Предел произведения конечного числа множителей равен произведению пределов этих множителей.
Теорема 3. Предел частного равен частному от деления пределов, если только предел знаменателя не равен нулю.
| 5.14. Теоремы о пределах (адрес файла Блок 4 ____). Теорема 1. Предел суммы конечного числа слагаемых равен сумме пределов этих слагаемых. Теорема 2. Предел произведения конечного числа множителей равен произведению пределов этих множителей. Теорема 3. Предел частного равен частному от деления пределов, если только предел знаменателя не равен нулю. Вернитесь к тексту |
Рассмотрим некоторые случаи, когда теоремы о пределах неприменимы. Особенно это часто бывает при отыскании предела отношения, когда предел знаменателя и числителя равны нулю или числитель и знаменатель стремятся к бесконечности, т.е. рассмотрим так называемые неопределенности вида
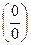и 
.
Пример 1. Найти
.
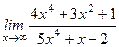Решение. При х ® ¥ числитель и знаменатель стремятся к бесконечности, то есть имеем отношение двух бесконечно больших величин. Чтобы «раскрыть» эту неопределенность (¥/¥), разделим числитель и знаменатель почленно на старшую степень х, то есть на х 4 и применим теоремы и пределах.
.
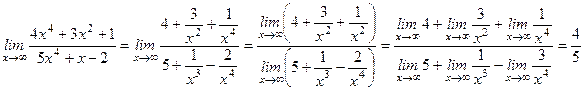Здесь величины
-
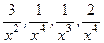бесконечно малые, следовательно, их предел равен нулю.
Пример 2. Найти
.
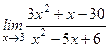Решение. При х ® 3 имеем неопределенность вида (0/0). Разложим числители и знаменатели на линейные множители.
3 х 2 + х – 30 = 0 х 1 = 3, 
х 2 – 5 х + 6 = 0 х = 2, х = 3
х 2 – 5 х + 6 = (х – 2) (х – 3)
Тогда
.
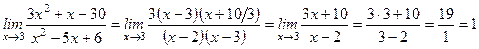Пример 3. Найти
.
Решение. Имеем неопределенность вида (0/0) при х ® -1. Избавимся от иррациональности в знаменателе, домножив числитель и знаменатель на выражение 
, сопряженное знаменателю.
.
Пример 4. Найти
.
Решение. Имеем неопределенность вида (0/0) при х ® 2. Избавимся от иррациональности в числителе, домножив числитель и знаменатель на неполный квадрат суммы
,
а знаменатель разложим на множители.
.
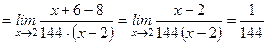Признак существования предела.
Теорема. Если значения функции f (х) заключены между соответствующими значениями функций F (х) и Ф (х), стремящихся при х ® х 0 к одному и тому же пределу А, то f (х) при х ® х 0 также имеет предел, равный числу А.
Доказательство. Пусть F (х) £ f (х) £ Ф (х) и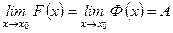 
. Докажем, что
. Возьмем произвольную e - окрестность числа А. По условию существует такая d - окрестность точки х 0, что соответствующие значения F (х) и Ф (х) принадлежат e - окрестности числа А, то есть
½ F (х) - А ½ < e ½ Ф (х) - А ½ < e или
А - e < F (х) < А + e
А - e < Ф (х) < А + e
Но тогда в силу заданных неравенств значения f (х), соответствующие точкам указанной d - окрестности точки х 0, также будут находиться в окрестности числа А, т.е. А - e < f (х) < А + e, а это значит, что 
.
Применим доказанный признак к выводу важного предельного соотношения
.
Этот предел часто называют первым замечательным пределом.
Первый замечательный придел (5.15).
Функция 
при a ® 0 имеет предел, равный 1: 
.
5.15. Первый замечательный придел (адрес файла Блок 4 ___).
Функция  при a ® 0 имеет предел, равный 1: .
Вернитесь к тексту
|
Доказательство.
| Будем исходить из геометрического определения синуса. Возьмем окружность радиуса 1 и предположим, что угол a, выраженный в радианах, заключен в границах 0 < a < p /2 (т.к. sin a / a является четной функцией, то достаточно рассмотреть случай, когда a > 0). Из рисунка видно, что площади треугольника ОАС, сектора ОАС и треугольника ОВС удовлетворяют соотношениям: |
SD ОАС < S сек. ОАС < SD ОВС
,
то
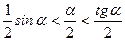или sin a < a < tg a
Разделим все члены неравенства на sin a (sin a > 0), получим
или 
.
Но т.к. 
, 
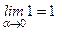, то
.
Рассмотрим примеры, где используется первый замечательный предел.
Пример 5. Найти
.
Решение. При х ® 0 имеем неопределенность вида (0/0). Чтобы воспользоваться первым замечательным пределом, разделим и умножим числитель на 3 х, а знаменатель – на 5 х.
.
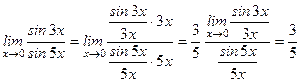Здесь
, 
.
Пример 6. Найти
.
Решение. Числитель и знаменатель при х ® 0 представляют собой бесконечно малые величины. Таким образом имеем неопределенность вида (0/0). Чтобы воспользоваться первым замечательным пределом, применим формулу 1 – cos 4 x = 2 sin 2 2 x. Тогда
.
Числитель разделим и умножим на 4 х 4, а знаменатель – на 64 х 3.
.