THE ROLE OF INFORMATION TECHNOLOGY AT THE DECISION MATRIX GAMES WITH MS EXCEL

УДК 004.8:6813.06(075.8)

Лукьянова Галина Викторовна / Lukyanova V. Galina

Кандидат технических наук, доцент/ PhD in technics, associate professor

Довлатян Галина Петровна / Dovlatian P. Galina

Кандидат экономических наук, доцент/ PhD in economics, associate professor

Лебедева Ольга Евгеньевна / Lebedeva E. Olga

Ключевые слова: информационные технологии, матричные игры, интерактивный метод

Keywords: information technology, matrix games, interactive method

В современном информационном обществе все большую роль играют информационные технологии и их управление для решения задач любой сложности. Целесообразно рассмотреть стратегически-необходимую теорию матричных игр, которая способна не только указать оптимальный путь к решению некоторых проблем, но и прогнозировать их исход. Матричные игры довольно просты, к ним могут быть сведены игры общего вида. Однако, в большинстве случаев решение представляет собой трудный и громоздкий процесс, выигрыши игроков в каждой ситуации не всегда определяются точными измерениями. В процессе сбора и анализа данных и введения при построении модели различных предположений накапливаются ошибки, точность в определении значения игры и оптимальных стратегий игроков не всегда оправдана. Погрешность в оценке игроком своего выигрыша не может привести к практически серьёзным последствиям и небольшое отклонение игрока от оптимальной стратегии не влечёт за собой существенного изменения в его выигрыше. В теории игр известны несколько способов приближенного решения матричных игр, на таких языках как: Turbo Pascal, Visual Basic, С + +.

Итеративный метод Брауна-Робинсона - метод приближённого решения матричных игр реализуется в MS Excel. Идея метода – многократное фиктивное разыгрывание игры Г_А с матрицей А={a_ij} размера (m´n). Одно разыгрывание игры - партия, число партий не ограниченно.

В 1-ой партии оба игрока выбирают произвольные чистые стратегии. Игрок 1 выбрал i-ю стратегию, а игрок 2 – j-ю стратегию. Во второй партии игрок 1 отвечает на ход игрока 2 той стратегией, которая даёт ему максимальный выигрыш. В свою очередь, игрок 2, отвечает на ход игрока 1 своей стратегией, которая обращает его проигрыш в минимум. Далее третья партия. С ростом числа шагов смешанные стратегии, которые приписываются игрокам, приближаются к их оптимальным стратегиям. Процесс приближённого нахождения оптимальных стратегий игроков называется итеративным, а его шаги – итерациями.

За первые k разыгрываний игрок 1 использовал i-ю чистую стратегию 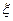_i^k раз (i=1,…,m), а игрок 2 j-ю чистую стратегию 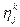раз (j=1,…,n). Тогда их смешанными стратегиями будут векторы .

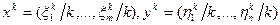Игрок 1 следит за действиями игрока 2 и с каждым своим ходом желает получить как можно больший выигрыш. В ответ на применение игроком 2 своей смешанной стратегии y ^k, он будет использовать чистую стратегию i_k+1, которая обеспечит ему лучший результат при разыгрывании (k+1)-ой партии. Игрок 2 поступает аналогично. В худшем случае каждый из них может получить:

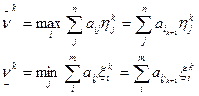
где 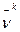- наибольшее значение проигрыша игрока 2 и 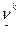- наименьшее значение выигрыша игрока 1.

Соотношения, определяющие средние значения проигрыша игрока 2 и выигрыша игрока 1:

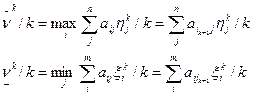
Если ν - цена матричной игры Г_А. Её значение будет больше выигрыша игрока 1, но меньше проигрыша игрока 2, т. е.

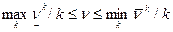. (1)

Таким образом, получен итеративный процесс, позволяющий находить приближённое решение матричной игры, при этом степень близости приближения к истинному значению игры определяется длиной интервала

.

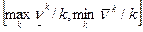Сходимость алгоритма гарантируется теоремой:

.

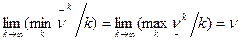Лемма. Для всякой матрицы А и "e>0 существует такое k₀, что

.

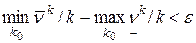При предельном переходе в неравенстве (1) при k®¥ имеем:

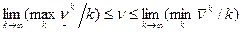. (2)

.

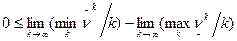Из леммы следует, что .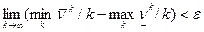

На основании неравенства (1) имеем: 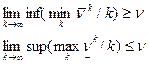. Следовательно, в силу ограниченности пределов .

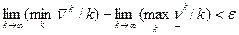оценка для разности пределов:

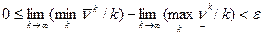для "e>0.

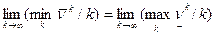. Из неравенства (2) следует, что равенство пределов = n.

Итак, .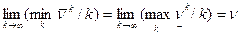

Приближённое решение игры с матрицей

А= 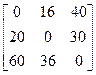, и пошаговая демонстрация решения в MS Excel

Шаг 1. На листе 1 создается матрица размерностью [3х3], игру начинает первый игрок (А1). Шаги в программе MS Excel выполняются автоматически согласно методу Брауна-Робинсона.

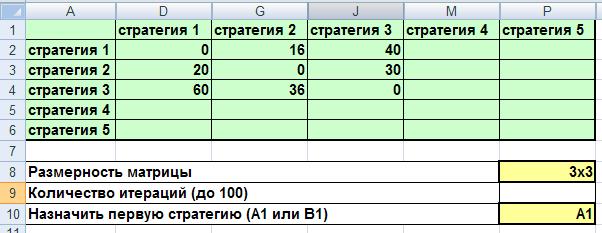
Рис.1

Шаг 2. Первый игрок произвольно выбирает одну из своих чистых стратегий. Предположим, что он выбрал свою 1-ю стратегию, а игрок 2 (В1), в результате расчетов стратегий, отвечает своей 1-й стратегией и

Расчет показателей первого игрока (А1), при n=1

Рис.2

Расчет показателей второго игрока (В1), при n=1

Рис.3

Замечание: В зависимости от того, какой из игроков начнет игру первым (игрок 1- А1 или игрок 2-В1), зависит расчет показателей на Рис.3:

Если игру начнет игрок А1, тогда накопленный выигрыш, противника, за первые n-шагов будет отображен в ячейках: AL14; AN14; AP14; AR14; AT14.

Если игру начнет игрок В1, тогда накопленный выигрыш, противника, за первые n-шагов будет отображен в ячейках: AM14; AO14; AQ14; AS14;AU14.

В столбце находится наименьший средний выигрыш равный 0 игрока 1, полученный им в первой партии; в столбце 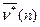стоит наибольший средний выигрыш равный 60, полученный игроком 2 в первой партии; в столбце n находится среднее арифметическое n=( + 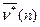)/2=30, т. е. приближенное значение цены игры.

Шаг 3. Из Рис. 3 следует: так как максимальное значение равное 60 соответствует 3-й стратегии игрока 2, значит, новая стратегия игрока 1 – 3-я стратегия и накопленный выигрыш первого игрока составит:

0+40=40 при его 1-й стратегии;

20+30=50 при его 2-й стратегии;

60+0=60 при его 3-й стратегии.

Из всех суммарных выигрышей наименьшим является 40, который получается при 3-й стратегии, следовательно, второй игрок должен взять именно эту стратегию для получения суммарного выигрыша в этой партии.

0+40=40 при его 1-й стратегии;

20+30=50 при его 2-й стратегии;

60+0=60 при его 3-й стратегии.

Из всех суммарных выигрышей второго игрока наибольшим является 60, который получается при 3-й стратегии, следовательно, первым игроком должна быть взята именно эта стратегия.

Расчет показателей первого игрока (А1), при n=2

Рис.4

Расчет показателей второго игрока (В1), при n=2

Рис.5

Все полученные данные занесены в таблицу (Рис.4, Рис.5). В столбце находится наименьший суммарный выигрыш игрока 1 за две партии, деленный на число партий, т. е. 20; в столбце 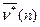находится наибольший суммарный выигрыш игрока 2, деленный на число партий, т. е. 30; в столбец n ставится среднее арифметическое этих значений, т. е. 25.

Продолжая процесс далее, возможно получить ряд разыгрываний игры за 100 итераций (партий), и приближённое решение игры: x¹⁰⁰ =(0,6; 0,01; 0,39), y¹⁰⁰ =(0,21; 0,3; 0,49), n=24.

Оптимальные стратегии для первого и второго игроков

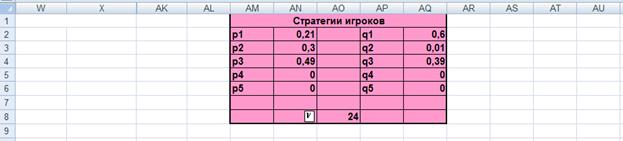
Рис.6

Представленная программа рассчитана на 16 матричных комбинаций:

(i х j), i = 2,..,5; j = 2,..,5. Вручную вводится матрица, ее размерность и MS Excel автоматически выдает ответ. Сходимость итераций, даже при небольшом расчете, дает возможность ориентировочного нахождения цены игры и доли частных стратегий, при увеличении же числа итераций решения значительно уточняются.