Преобразование координат при замене базиса.
Пусть системы векторов e = {e 1,..., e n } и f = {f 1,..., f n } — два базиса n -мерного линейного пространства Ln.
Обозначим xe = (x 1, x 2,..., xn) и xf = (x' 1, x' 2,..., x'n) — координаты вектора x ∈ Ln соответственно в базисах e и f.
Справедливо следующее xe = Ce→f·xf:

Здесь Ce→f — матрица перехода от базиса e к базису f, это матрица, столбцами которой являются координаты базисных векторов f1,..., f n в базисе e 1,..., e n:
f1 = с 11· e2 + с 21 · e1 +... + сn 1 · e n, f2 = с 12· e1 + с 22 · e2 +... + сn 2 · e n, ..., f n = с 1 n · e2 +... + сnn · e n.
Формулу преобразования координат вектора при изменении базиса принято записывать в виде
xf = (Ce→f)− 1·xe
ИЛИ
Пусть в 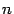 -мерном линейном пространстве
-мерном линейном пространстве 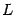 выбран базис
выбран базис 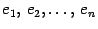 , который мы будем для удобства называть "старый" и другой базис
, который мы будем для удобства называть "старый" и другой базис 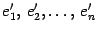 , который мы будем называть "новый". Возьмем призвольный вектор
, который мы будем называть "новый". Возьмем призвольный вектор 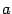 из
из 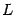 . Его координатный столбец в старом базисе обозначим
. Его координатный столбец в старом базисе обозначим 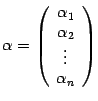 , а в новом --
, а в новом -- 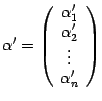 . Нам нужно выяснить, как связаны друг с другом координаты в старом и в новом базисе. Для этого нам сначала нужно "связать" друг с другом старый и новый базисы. Запишем разложения новых базисных векторов по старому базису
. Нам нужно выяснить, как связаны друг с другом координаты в старом и в новом базисе. Для этого нам сначала нужно "связать" друг с другом старый и новый базисы. Запишем разложения новых базисных векторов по старому базису

Составим матрицу, столбцами которой служат координатные столбцы векторов нового базиса

Эта матрица называется матрицей перехода от старого базиса к новому.
Критерий линейной независимости строк (столбцов).
Любые столбцы, входящие в линейно независимую систему, образуют линейно независимую подсистему.
Если система столбцов 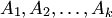 — линейно независима, а после присоединения к ней столбца
— линейно независима, а после присоединения к ней столбца 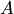 — оказывается линейно зависимой, то столбец
— оказывается линейно зависимой, то столбец 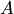 можно разложить по столбцам
можно разложить по столбцам 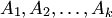 , и притом единственным образом, т.е. коэффициенты разложения находятся однозначно.
, и притом единственным образом, т.е. коэффициенты разложения находятся однозначно.
В предыдущем разделе были введены операции умножения матриц на число и сложения матриц, в частности, для матриц-столбцов 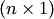 и матриц-строк
и матриц-строк 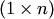 . Матрицы-столбцы (матрицы-строки) будем называть далее просто столбцами (соответственно строками) и обозначать в этой главе прописными буквами. При помощи этих операций можно составлять некоторые алгебраические выражения. Напомним, что равными считаются столбцы одинаковых размеров с равными соответствующими элементами.
. Матрицы-столбцы (матрицы-строки) будем называть далее просто столбцами (соответственно строками) и обозначать в этой главе прописными буквами. При помощи этих операций можно составлять некоторые алгебраические выражения. Напомним, что равными считаются столбцы одинаковых размеров с равными соответствующими элементами.
Столбец 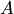 называется линейной комбинацией столбцов
называется линейной комбинацией столбцов 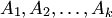 одинаковых размеров, если
одинаковых размеров, если
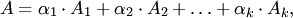
| (3.1) |
где 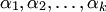 — некоторые числа. В этом случае говорят, что столбец
— некоторые числа. В этом случае говорят, что столбец 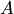 разложен по столбцам
разложен по столбцам 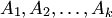 , а числа
, а числа 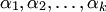 называют коэффициентами разложения. Линейная комбинация
называют коэффициентами разложения. Линейная комбинация 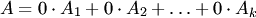 с нулевыми коэффициентами называется тривиальной.
с нулевыми коэффициентами называется тривиальной.
Если столбцы в (3.1) имеют вид
то матричному равенству (3.1) соответствуют поэлементные равенства
Аналогично формулируется определение линейной комбинации строк одинаковых размеров.
Набор столбцов 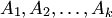 одинаковых размеров называется системой столбцов.
одинаковых размеров называется системой столбцов.
Система из 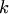 столбцов
столбцов 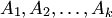 называется линейно зависимой, если существуют такие числа
называется линейно зависимой, если существуют такие числа 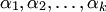 , не все равные нулю одновременно, что
, не все равные нулю одновременно, что

Здесь и далее символом о обозначается нулевой столбец соответствующих размеров.
Система из 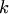 столбцов
столбцов 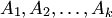 называется линейно независимой, если равенство (3.2) возможно только при
называется линейно независимой, если равенство (3.2) возможно только при  , т.е. когда линейная комбинация в левой части (3.2) тривиальная. Аналогичные определения формулируются и для строк (матриц-строк).
, т.е. когда линейная комбинация в левой части (3.2) тривиальная. Аналогичные определения формулируются и для строк (матриц-строк).
Замечания 3.1
1. Один столбец 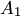 тоже образует систему: при
тоже образует систему: при 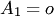 — линейно зависимую, а при
— линейно зависимую, а при 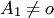 линейно независимую.
линейно независимую.
2. Любая часть системы столбцов называется подсистемой.
Пример 3.1. Используя определение, установить линейную зависимость или линейную независимость систем столбцов
Решение. 1) Столбцы 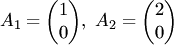 линейно зависимы, так как можно составить нетривиальную линейную комбинацию, например, с коэффициентами
линейно зависимы, так как можно составить нетривиальную линейную комбинацию, например, с коэффициентами 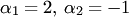 , которая равна нулевому столбцу:.
, которая равна нулевому столбцу:.
2) Столбцы 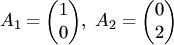 линейно независимы, так как равенство
линейно независимы, так как равенство
равносильное системе 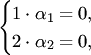
оказывается верным только при 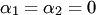 .
.