Аннотация
Книга предназначена для школьников старших классов, студентов физико-математических факультетов, учителей и любителей математики. В книге приведены в рамках элементарных математических знаний, за исключением метода сравнения чисел по модулю, доказательства Великой теоремы Ферма для простых показателей вида 6n + 1 и для простых показателей вида 6n + 5.
Введение
Утверждение великого французского математика Пьера Ферма (1601 – 1665) о том, что неопределенное уравнение Xn + Yn = Zn не имеет решений в целых (не равных нулю) рациональных числах для n > 2 признано мировым математическим сообществом верным, после представления в 1995 г. его доказательства группой математиков Оксфордовского университета во главе с английским математиком Эндрю Уайльсом.
Это утверждение великого француза, получившее название Проблема Ферма или Великая теорема Ферма (она же «Большая» или «Последняя»), более чем 300 лет оставалось проблемной задачей теории чисел. Свое УтверждениеПьер Ферма написал на полях книги Диофанта «Арифметика» и сопроводил его следующим известным комментарием: “Я открыл этому поистине чудесное доказательство, которое из-за недостатка места не может разместиться на этих полях”.[3]
Этот комментарий Пьера Ферма (учитывая его авторитет) указывал на возможность решения Проблемы в рамках математических знаний XVII века, это обстоятельство и другие, социально – психологические причины, толкали сотни любителей математики на поиск элементарного решения Великой теоремы.
Проблема Ферма вышла за пределы математического сообщества, стала популярной, привлекая к себе не только сотни любителей математики, но и представителей культуры, которые сделали ее неким украшением художественных героев.
Показанный С.П. Капица фильм «Черт и математик» в одной из передач «Очевидное – Невероятное» в начале 70-х годов прошлого столетия и его комментарий послужили толчком моего увлечения этой Проблемой.
В основе настоящей работы лежит моя книжка “Проблема Ферма и другое”2008 г. выпуска, в которой отсутствовало доказательство ПФ 2-го случая для простых показателей вида 6n + 5.
Известно, что для показателя n = 4 Проблема решена Пьером Ферма, а для показателя n = 3 доказана гениальным Леонардом Эйлером, а потому я стал искать решение приведенного уравнения для простых показателей P> 3 т.е. для простых показателей вида 6n + 5 и вида 6n = 1.
Элементарные алгебраические преобразования многочленов, вспомогательные числа, и вспомогательные сравнения позволили найти элементарное доказательство Проблемы, если не считать примененный в работе метод сравнения чисел по модулю, введенный в математику К.Ф.Гауссом (1777 – 1855).
1. Проблемы Ферма для простых показателей > 3
Доказательство Великой теоремы для простых показателей вида 6n + 1 и для простых показателей вида 6n + 5
Множество простых чисел > 3 разбиваем на два класса: на класс простых чисел вида 6n + 1 и на класс простых чисел вида 6n + 5.
Докажем сначала вспомогательные утверждения.
1.1 Вспомогательные утверждения
Теорема 1.1. Для любого простого числа P > 2 существуют целые числа, которые обозначим через А1, А2, А3, …, Ar, …, АP–1/2, такие, что для любых чисел Z и X выполняется:
ZP – XP = (Z – X)P + A1ZX(Z – X)P–2 + A2Z 2X 2(Z – X)P–4 +
+ A3Z 3X 3(Z – X)P–6 + А4Z 4X 4(Z – X)Р–8+ … +AР–3/2 ´
´ ZP–3/2XP–3/2(Z – X)3 + AP–1/2 ZР–1/2 XР–1/2 (Z – X), (1.1)
при этом числа A1 = AР–1/2 = P, а числа А2, А3,…, Ar, …, АР–3/2 – целые и кратные Р. Доказательство. Пусть имеем многочлен вида
(Z – X)P–1 + A1ZX (Z – X)P–3 + A2Z 2 X 2 (Z – X)P–5 +
+ А3Z 3 X 3 (Z – X)P-7+ A4Z 4 X 4 (Z – X)Р–9+…... + AР–3/2 Z P–3/2 X Р–3/2 (Z – X)2 + AР–1/2Z Р–1/2 X P–1/2. (1.2)
Покажем, что существуют такие целые числа (кратные Р) A1, A2, …, AР–1/2, что многочлен (1.2) тождественно равен многочлену вида:
Z P–1 + Z P–2X + Z P–3X 2 + …+ Z 2X P–3 + ZX P–2 + X P–1. (1.3)
Пусть многочлены (1.2) и (1.3) тождественно равны, тогда их коэффициенты при подобных членах будут равны.
Чтобы сравнить коэффициенты при подобных членах многочленов (1.2) и (1.3) воспользуемся табл. 1. Благодаря равенству биноминальных коэффициентов от начала и конца разложения бинома Ньютона в табл. 1 внесены коэффициенты от начала разложения соответствующих биномов многочлена (1.2) до серединного их члена (включительно) (строки 1,..., Р + 1/2).
В строке 1 записаны биноминальные коэффициенты разложения бинома (Z – X)P–1.
В строке 2 (начиная со столбца 2) записаны биноминальные коэффициенты разложения бинома (Z – X)P–3, умноженные на число А1.
В строке 3 (начиная со столбца 3) записаны биноминальные коэффициенты разложения бинома (Z – X)P–5, умноженные на число А2 и т. д.
B строке (Р–1)/2 записаны (начиная со столбца (Р–1)/2)биноминальные коэффициенты разложения бинома (Z–X)2, умноженные на число АР–3/2.
В строке (Р+1)/2 записан коэффициент последнего члена многочлена (1.2) – число АР–1/2.
В последней строке табл. 1 записаны коэффициенты многочлена (1.3), которые равны +1.
Обратим внимание на то, что в каждом столбце табл. 1 (до строки Р + 1/2 включительно) записаны все коэффициенты подобных членов многочлена (1.2), а в строке без номера записаны коэффициенты членов многочлена (1.3).
Это обстоятельство позволяет вычислять числа А1, А2, …
Суммируя последовательно коэффициенты столбцов табл. 1 от столбца 2 до столбца (Р + 1)/2 и приравнивая полученные суммы (в силу тождества (1.2) и (1.3)) к (+1), получим значения чисел А1, А2,
Из столбца 2 получим 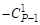 + А1 = 1, тогда А1 =
+ А1 = 1, тогда А1 =  + 1, отсюда
+ 1, отсюда
А1 = Р. (1.4)
 Таблица 1.Таблица коэффициентов
Таблица 1.Таблица коэффициентов
| . | . | … | … | p – 1/2 | P + 1/2 | ||||||
| +1 | 
| 
| 
| 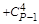
| . | . | . | . | … | 
| |
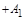
| 
| 
| 
| . | . | . | . | … | 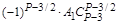
| ||

| 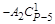
| 
| . | . | . | . | … | 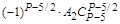
| |||

| 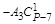
| . | . | . | . | … | 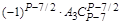
| ||||

| . | . | . | . | … | 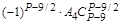
| |||||
| . | . | . | . | . | … | ||||||
| . | . | . | . | … | |||||||
| . | . | . | … | ||||||||
| . | . | … | |||||||||
| P–1/2 | 
| 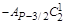
| |||||||||
| P+1/2 | 
| ||||||||||
| + 1 | + 1 | + 1 | + 1 | + 1 | . | . | . | . | + 1 | + 1 |
Из столбца 3 (с учетом (1.4)) получим +  –
–  + А2 = 1, отсюда А2 =
+ А2 = 1, отсюда А2 =  – (
– ( – 1) = Р(Р – 3)/2, а значит, А2 – число целое и кратное Р.
– 1) = Р(Р – 3)/2, а значит, А2 – число целое и кратное Р.
Для доказательства того, что А3 – число целое и кратное Р, достаточно определить, что (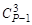 + 1) – число кратно Р, (то, что оно целое очевидно) так как остальные коэффициенты столбца 4 – числа целые и кратные Р, множители А1 и А2 которых, как показано выше, целые и кратные Р. Далее,
+ 1) – число кратно Р, (то, что оно целое очевидно) так как остальные коэффициенты столбца 4 – числа целые и кратные Р, множители А1 и А2 которых, как показано выше, целые и кратные Р. Далее, 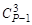 + 1 = Р(Р2 – 6Р + 11)/6 – число кратное Р, так как при Р = 6n + 1 или Р = 6n + 5 дробь (Р2 – 6Р + 11)/6 - целое число, где n = Î N+, а значит А3 – число целое и кратное Р.
+ 1 = Р(Р2 – 6Р + 11)/6 – число кратное Р, так как при Р = 6n + 1 или Р = 6n + 5 дробь (Р2 – 6Р + 11)/6 - целое число, где n = Î N+, а значит А3 – число целое и кратное Р.
Если нами найдено, что А1, А2, …, Аk –1 – числа целые и кратные Р, то число Аk будет целым и кратным Р, если  – число кратное Р (то, что оно целое очевидно), где k = 1, 2, …, P–1/2. Пусть k – число четное, тогда имеем
– число кратное Р (то, что оно целое очевидно), где k = 1, 2, …, P–1/2. Пусть k – число четное, тогда имеем  – целое и кратное Р, так как
– целое и кратное Р, так как  = (P – 1)(P – 2)…(P – k)/k! – 1= (mP + k!)/k! – 1 = mP/k! – число целое и кратное Р, где (m, P)=1 и m кратное k!
= (P – 1)(P – 2)…(P – k)/k! – 1= (mP + k!)/k! – 1 = mP/k! – число целое и кратное Р, где (m, P)=1 и m кратное k!
Пусть k – число нечетное, тогда имеем –  – число кратное Р(то, что оно целое очевидно), так как
– число кратное Р(то, что оно целое очевидно), так как  = (P – 1)(P – 2)…(P – k)/k! + 1 = (m1P – k!)/k! + 1 =m1P/k!- – число целое и кратное Р, где (m1,P)=1 и m1 кратно k!
= (P – 1)(P – 2)…(P – k)/k! + 1 = (m1P – k!)/k! + 1 =m1P/k!- – число целое и кратное Р, где (m1,P)=1 и m1 кратно k!
Таким образом, при любой четности k число Аk будет числом целым и кратным Р.
Осталось доказать, что число АР–1/2 = Р.
Пусть Z = X = 1, тогда многочлен (1.2) будет равен АР–1/2, а многочлен (1.3) равен Р и их тождество возможно, если
АР–1/2 = Р. (1.5)
Запишем тождество многочленов (1.2) и (1.3) с учетом (1.4) и (1.5):
ZP–1 + Z P–2 X + ZP–3 X 2 + Z 2X P–3 + ZX P–2 + Z P–1 =
= (Z – X) P–1 + PZX (Z – X)P–3 + A2Z 2X 2(Z – X) P–5 +…
+ AP–3/2 Z P–3/2 X P–3/2(Z – X)2 + PZ P–1/2 X P–1/2. (1.6)
Умножая правую и левую части тождества (1.6) на (Z – X), получим (1.1), что и требовалось доказать. Следствие. Если Z и X натуральные взаимно простые числа и ZP – XP = (Z – X) M1, то
a) (Z – X, M1) = 1, если (Z – X, P) = 1;
б) (Z – X, M1) = P, если (Z – X, P) =P,
где M1 – многочлен вида (1.3) и для б) M1= G1P, (G1,P) = 1.
Так как Z P + X P = Z P – (– X) P= [Z – (– X)] M2, то
M2 = Z P–1 – Z P–2X + Z P–3X 2 –…+ Z 2X P–3 – ZX P–2 +X P–1 =
= (Z + X) P–1 – PZX (Z + X)P–3 + A2Z 2X 2 (Z + X) P–5 –
– A3Z 3X 3 (Z + X) P–7 + ……….+ (–1)P–1/2 P (ZX) P–1/2, (1.7)
тогда:
г) (Z + X, M2) = 1, если (Z + X, P) = 1,
д) (Z + X, M2) = P, если (Z + X, P) = P,
где для д) М2 = G2P, (G2, P) = 1.
Теорема 1.2. Для любого простого числа Р > 3 существуют целые числа, которые обозначим через В1, В2, Вi, …, Вn1 такие, что для любых чисел Z и X выполняется:
(Z – X) P–3 +  ZX (Z – X) P–5 +
ZX (Z – X) P–5 +  Z 2X 2(Z – X) P–7 +…
Z 2X 2(Z – X) P–7 +…  Z P–5/2X P–5/2 (Z – X)2 + (ZX)P–3/2 = [(Z – X)2 + ZX)]P–3/2+ В1Z 2X 2 (Z – X)2 [(Z – X)2 + ZX]P–9/2 + B2Z 4X 4(Z – X)4[(Z – X)2 + ZX]P–15/2 +…+BiZ 2iX 2i (Z – X)2i [(Z – X)2 + ZX] R +…+ Вn1Z 2n1 X 2n1 (Z – X)2n1 [(Z – X)2 + ZX] S, (1.8)
Z P–5/2X P–5/2 (Z – X)2 + (ZX)P–3/2 = [(Z – X)2 + ZX)]P–3/2+ В1Z 2X 2 (Z – X)2 [(Z – X)2 + ZX]P–9/2 + B2Z 4X 4(Z – X)4[(Z – X)2 + ZX]P–15/2 +…+BiZ 2iX 2i (Z – X)2i [(Z – X)2 + ZX] R +…+ Вn1Z 2n1 X 2n1 (Z – X)2n1 [(Z – X)2 + ZX] S, (1.8)
где  = А2/Р,
= А2/Р,  = А3/Р, …,Ak1 = Ak/P, …,
= А3/Р, …,Ak1 = Ak/P, …, 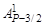 = АР– 3/2/Р,
= АР– 3/2/Р, 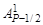 = =
= = 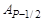 /P = 1.
/P = 1.
Здесь Аk – коэффициенты полиномов Чебышева. Обратим внимание на то, что разница показателей степеней любых двух соседних чисел в квадратных скобках правой части (1.8) равна |3|, тогда Р – 3/2 = = 3n1 + s, где s – число натуральное < 3, а R = P – 3/2 – 3i. Пусть Р = 6n + 1, тогда Р – 3/2 = (6n + 1 – 3)/2 = 3 (n – 1) + 2 = 3n1 + s, отсюда s = 2, а n1 = n – 1.
Пусть Р = 6n + 5, тогда Р – 3/2 = (6n + 5 – 3)/2 = 3n + 1 = 3n1 + s, отсюда s = 1, а n1 = n.
Доказательство. Доказательство будет аналогично доказательству теоремы 1.1.
Пусть ZX = V, (Z – X)2 = U, тогда (1.8) будет иметь вид
U P–3/2 +  VUP–5/2 +
VUP–5/2 +  V 2UP–7/2 +…+
V 2UP–7/2 +…+ 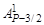 VР–5/2U + VP–3/2 =
VР–5/2U + VP–3/2 =
= (U + V)P–3/2 + B1V 2U (U + V)P–9/2 + B2V 4U 2 (U + V) P–15/2 + …
…+ BiV 2iU i (U + V)R … Вn1V 2n1U n1(U + V)S. (1.9)
Покажем, что существуют такие целые числа В1, В2, …, Bi,..., Вn1, что равенство (1.9) справедливо.
Пусть левая часть формулы (1.9) тождественно равна ее правой части, тогда их коэффициенты при подобных членах равны.
Чтобы сравнить коэффициенты (значит, найти Вi) при подобных членах левой и правой частей (1.9), воспользуемся табл. 2.
В строке 1 записаны биноминальные коэффициенты разложения бинома (U + V)P–3/2.
В строке 2 (начиная со столбца 3) записаны биноминальные коэффициенты разложения бинома (U + V)P–9/2, умноженные на число В1.
В строке 3 (начиная со столбца 5) записаны биноминальные коэффициенты разложения бинома (U + V)P–15/2, умноженные на число В2.
В строке n1 + 1 записаны биноминальные коэффициенты разложения последнего бинома (U + V)S, умноженные на число Вn1.
В последней строке табл. 2 записаны коэффициенты левой части (1.9).
В каждом столбце табл. 2 (до строки n1 + 1) записаны все коэффициенты подобных членов правой части (1.9). Это обстоятельство позволяет последовательно вычислять числа В1, В2, …, Вi, …, Bn1. суммируя коэффициенты столбца и приравнивая полученную сумму к  , находим В1, далее, суммируя коэффициенты столбца 5 и приравнивая полученную сумму к
, находим В1, далее, суммируя коэффициенты столбца 5 и приравнивая полученную сумму к 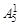 , находим В2 и т. д.
, находим В2 и т. д.
Из столбца 3 следует, что  + В1 =
+ В1 =  , отсюда В1 – число целое, так как
, отсюда В1 – число целое, так как 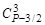 и
и  числа целые.
числа целые.
Из столбца 5 следует, что 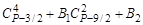 =
= 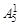 , отсюда В2 – число целое, так как остальные числа этого равенства целые.
, отсюда В2 – число целое, так как остальные числа этого равенства целые.
Из столбца 7 следует, что  =
=  , отсюда В3 число целое, так как остальные числа этого равенства целые, и т.д.
, отсюда В3 число целое, так как остальные числа этого равенства целые, и т.д.
Из столбца (3 + 2i) следует, что число Вi+1 целое, так как числа В1, В2, …, Вi целые.
Обратим внимание, что в каждом последующем столбце (3 + 2i) числа В1, В2, …, Вi+1 целые, где i = 0, 1, 2, …, n1-1, а значит, из столбца [3 + 2(n1 – 1)] следует, что Вn1 – число целое.
Таким образом, доказано, что существуют такие целые числа В1, В2, Bn1 и левая часть (1.9) тождественно равна правой части (1.9), а значит, и левая часть (1.8) тождественно равна правой части (1.8).
Запишем (1.8) для степени Р вида 6n + 1, принимая во внимание, что s = 2.
(Z – X)P–3 + 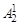 ZX(Z – X)P–5 +
ZX(Z – X)P–5 + 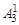 Z 2X 2(Z – X)P–7 +…...+
Z 2X 2(Z – X)P–7 +…...+  ZP–5/2 XP–5/2(Z – X)2 + ZP–3/2XP–3/2 = [(Z – X)2 + ZX]2 W, (1.10)
ZP–5/2 XP–5/2(Z – X)2 + ZP–3/2XP–3/2 = [(Z – X)2 + ZX]2 W, (1.10)
где W = [(Z – X)2 + ZX)]P–7/2 + B1Z 2X 2(Z – X)2 [(Z – X) + ZX]P–13/2 + B2Z 4X 4(Z – X)4[(Z – X)2 + ZX)]P–19/2 + …+ Bi Z 2iX 2i (Z – X)2i [(Z – X)2 + ZX]R–2 + Bn1Z 2n1 X 2n1 (Z –X)2n1.
Следствие. Пусть X = – X0, а Z = Z0, где (X0, Z0) Î N +, тогда
(Z0 + X0)P–3 – 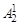 Z0X0 (Z0 + X0)P–5+
Z0X0 (Z0 + X0)P–5+  (Z0 + X0)P–7 –…
(Z0 + X0)P–7 –…
...+ (–1)P–3/2  = [(Z0 + X0)2 – Z0X0]2 W0, (1.11)
= [(Z0 + X0)2 – Z0X0]2 W0, (1.11)
где W0 имеет форму многочлена W.
Таблица 2.Таблица коэффициентов

| 
| 
| 
| 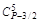
| 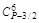
| ||||||||||
| B1 | 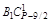
| 
| 
| 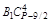
| |||||||||||
| B2 | 
| 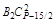
| |||||||||||||
| B3 | |||||||||||||||
| . | |||||||||||||||
| n1 + 1 | |||||||||||||||
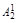
| 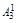
| 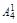
| 
| 
| 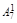
| ||||||||||
| … | 3 + 2(n1- 1) | … | P–9/2 | P–7/2 | P–5/2 | P–3/2 | P–1/2 | ||||||||

| … | … | … | 
| 
| 
| 
| ||||||||

| … | … | … | 
| 
| 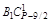
| B1 | ||||||||

| … | … | … | 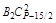
| 
| B2 | |||||||||
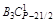
| … | … | … | 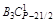
| B3 | ||||||||||
| … | … | … | B4 | ||||||||||||
| . | … | … | |||||||||||||
| n1 + 1 | … | 
| … | ||||||||||||
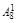
| … | … | … | 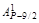
| 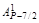
| 
| 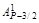
| ||||||||
1.2 Основная теорема
Теорема: Неопределенное уравнение X P + Y P = Z P не имеет решений в натуральных числах, где P – простое число >3.
Доказательство ведем от противного.
Пусть существует решение неопределенного уравнения
X P + Y P = Z P (1.12)
в натуральных числах и пусть это решение примитивное, т.е.
(X, Y) = 1, (Z, X) = 1, (Z, Y) = 1. (1.13)
1.3 Основные обозначения и соотношения
Все вводимые ниже числа принадлежат N +.
Благодаря (1.12) и (1.13) одно из чисел (X, Y и Z) четное.
Пусть
d0 = НОД+(X + Y, Z) Þ пусть X + Y = C0d0, (1.14)
а Z = a0d0, (1.15)
где (a0, С0) = 1; (1.16)
d1 = НОД+(Z – X, Y) Þ пусть Z – X = C1d1, (1.17)
а Y = a1d1, (1.18)
где (a1, C1) = 1; (1.19)
d2 = НОД+(Z – Y, X) Þ пусть Z – Y = C2d2, (1.20)
а X = a2d2, (1.21)
где (a2, С2) = 1. (1.22)
Благодаря (1.13) (d0, d1) = 1, (d0, d2) = 1 и (d2, d1) = 1.
Запишем трехчлен (X + Y – Z) в трех формах и, учитывая (1.14) и (1.15), (1.17) и (1.18), (1.20) и (1.21), получим соответственно:
(X + Y) – Z = C0d0 – a0d0 = d0(C0 – a0), (1.23)
Y – (Z – X) = a1d1 – C1d1 = d1(a1 – C1), (1.24)
X – (Z – Y) = a2d2 – C2d2 = d2(a2 – C2). (1.25)
С учетом условия п. 1.3.3 и равенств (1.23), (1.24) и (1.25) будет справедливо равенство и сравнение
X + Y – Z = K d0d1d2, Þ X + Y – Z º 0 mod K (1.26)
где K > 3 (докажем ниже).
Решая совместно (1.26) и (1.23), (1.26) и (1.24), (1.26) и (1.25), получим соответственно:
С0 – a0 = K d1d2, (1.27)
a1 – C1 = K d0d2, (1.28)
a2 – C2 = K d0d1. (1.29)
Из равенства (1.27) с учетом условия (1.16) следует, что (a0,K) =1 и (C0,K) = 1, но тогда и (Z,K) = 1.
Из равенства (1.28) с учетом условия (1.19) следует, что (a1,K) =1 и (C1,K) = 1, но тогда и (Y,K) = 1.
Из равенства (1.29) с учетом условия (1.21) следует, что (a2,K) =1 и (C2,K) = 1, но тогда и (X,K) = 1.
Так как число K попарно взаимно простое с числами X, Y и Z, а одно из этих чисел четное (п.1.3.1.), то K – число нечетное.
В дальнейшем мы будем использовать числа K и K2 в качестве модулей вспомогательных сравнений, для чего ниже будет дано углубленное представление об числе K.
1.4 Формулы Абеля в наших обозначениях и их связь с другими установленными соотношениями
Для 1-го случая Проблемы Ферма (далее ПФ), т.е. когда (X, P) = 1, (Z, P) = 1, (Y, P) = 1, формулы Абеля и основные соотношения(1.3.2) будут связаны соответственно:
X + Y =  =C0d0, отсюда С0=
=C0d0, отсюда С0= 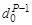 , (1.30)
, (1.30)
Z – X =  = C1d1, отсюда С1 =
= C1d1, отсюда С1 = 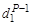 , (1.31)
, (1.31)
Z – Y =  = C2d2, отсюда C2 =
= C2d2, отсюда C2 =  ; (1.32)
; (1.32)
X P–1 – X P–2 Y + …– XY P–2 + Y P–1 =  , (1.33)
, (1.33)
Z P–1 + Z P–2 X + …+ ZX P–2 + X P–1 = 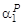 , (1.34)
, (1.34)
Z P–1 + Z P–2 Y +…+ ZY P–2 + Y P–1 = 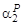 . (1.35)
. (1.35)
Для 2-го случая ПФ ограничимся вариантом, когда
(Z, P) = P, (X, P) = 1, (Y, P) = 1, в этом случае формулы Абеля и основные соотношения (1.3.2) будут связаны соответственно:
X + Y =  /P = C0d0,
/P = C0d0,
C0 = d0P -1/P, (1.36)
Левые части формул Абеля (1.33),(1.34),(1.35) и (1.37), запишем с учетом (1.7) и (1.6) – теоремы 1.1.,, а также с учетом (1.11) теоремы 1.2.вынося PXY за квадратные скобки:
С учетом теоремы 1.1.
(X + Y)P–1 – PXY [(X + Y)P–3 + 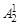 XY(X +Y)P–5 +…+(–1)P–5/2
XY(X +Y)P–5 +…+(–1)P–5/2  X P–5/2 Y P–5/2 (X + Y)2 + (–1)P–3/2X P–3/2Y P–3/2 ] =
X P–5/2 Y P–5/2 (X + Y)2 + (–1)P–3/2X P–3/2Y P–3/2 ] =  [ для (1.33)], (1.38)
[ для (1.33)], (1.38)
(Z - X)P–1 + PZX [(Z - X)P–3 + 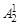 ZX(Z - X)P–5
ZX(Z - X)P–5  Z P–5/2 X P–5/2 (Z - X)2 + Z P–3/2 X P–3/2 ] =
Z P–5/2 X P–5/2 (Z - X)2 + Z P–3/2 X P–3/2 ] =  [ для (1.34)], (1.39)
[ для (1.34)], (1.39)
(Z - Y)P–1 + PZY [(Z - Y)P–3 + 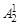 ZY(Z - Y)P–5 +…
ZY(Z - Y)P–5 +…  Z P–5/2 Y P–5/2 (Z - Y)2 + ZP–3/2Y P–3/2 ] =
Z P–5/2 Y P–5/2 (Z - Y)2 + ZP–3/2Y P–3/2 ] =  [ для (1.35)], (1.40)
[ для (1.35)], (1.40)
(X + Y)P–1 – PXY [(X + Y)P–3 – 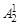 XY(X +Y)P–5 + –1)P–5/2
XY(X +Y)P–5 + –1)P–5/2  X P–5/2 Y P–5/2 (X + Y)2 + (–1)P–3/2X P–3/2Y P–3/2 ] = P
X P–5/2 Y P–5/2 (X + Y)2 + (–1)P–3/2X P–3/2Y P–3/2 ] = P  [для (1.37)], (1.41)
[для (1.37)], (1.41)
(X + Y)P -1 – PXY [(X + Y)2 – XY]S 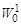 =
=  [для (1.33)]; (1.42)
[для (1.33)]; (1.42)
(X + Y)P -1 – PXY [(X + Y)2 – XY]S 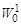 =
= 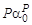 [для (1.37)], (1.43)
[для (1.37)], (1.43)
(Z - X)P -1 +PZX [(Z - X)2 + ZX]SW11 = a1P [для (1.34)];
(Z - Y)P -1 + PZY [(Z - Y)2 + ZY]SW21= a2P [для (1.35)];
А принимая во внимание, что с учетом(1.30) и (1.36) степень
(X + Y)P –1 = (C0d0)P –1 =C0P - для 1- го случая ПФ и
(X + Y)P –1 = (C0d0)P –1 = PC0P – для 2 –го случая ПФ.
Тогда последние равенства для формул Абеля (1.33) и (1.37) будут:
C0P– PXY [(X + Y)2 – XY]S 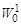 =
=  [для (1.33)],
[для (1.33)],
PC0P– PXY [(X + Y)2 – XY]S 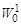 =
= 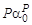 [для (1.37)],
[для (1.37)],
из которых следуют [для (1.33)], PXY [(X + Y)2 – XY]S 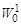 = C0P - a0P, (1.44)
= C0P - a0P, (1.44)
[для (1.37)], PXY [(X + Y)2 – XY]S 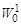 = P(C0P - a0P),
= P(C0P - a0P),
а после сокращения на P
XY [(X + Y)2 – XY]S 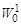 = (C0P - a0P), (1.45)
= (C0P - a0P), (1.45)
где 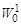 соответствует W0 и W11, W21соответствуют W [cм. (1.11)] теоремы 1.2., а
соответствует W0 и W11, W21соответствуют W [cм. (1.11)] теоремы 1.2., а
s = 1 для P вида 6n + 5,
s = 2 для P вида 6n + 1.
Таким образом мы установили связь формул Абеля и полученных нами соотношений.
Далее о модуле K, а затем используя вспомогательные числа и вспомогательные сравнения по модулю K, доказательство того, что
(X + Y)2 – XYº 0 mod K, (Z – X)2 + ZX º 0 mod K, ( Z – Y)2 + ZYº 0 mod K.
Модуль K
Дальнейшие рассуждения требуют расширенного представления о модуле K.
Нижепокажем:
---- что для 1-го случая ПФ модуль K =eP2;
---- чтодля 2-го случая ПФ модуль K >3; ----- что для 2-го случая ПФ имеет место (K,P) = 1;
---- что простые числа вида 6n + 5, не могут быть делителями K (см. в разделе 1.7.);
--- что числа 3t, где t > 1, не могут быть делителями K (см.в разделе1.7.).
а) Для доказательства того, что K = eP2 для 1-го случая ПФ,
из равенств (1.38), (1.39) и (1.40) находим, что
(X + Y)P –1 º a0P mod P,
(Z – X)P –1 º a1P mod P,
(Z – Y)P –1 º a0P mod P, тогда благодаря Малой теореме Ферма имеем
a0P º 1 mod P, Þ a0P º 1 mod P2, Þ a0 = e0P + 1,
a1P º 1 mod P, Þ a1P º 1 mod P2, Þa1 = e1P + 1,
a2P º 1 mod P, Þ a2P º 1 mod P2, Þa2 = e2P + 1.
Очевидно, что XP + YP – ZP º 0 mod P2
Тогда, с учетом последних сравнений и равенств (1.15), (.18) и (1.21) имеем
a2Рd2P + a1PdP - a0Pd0P º. d0P – d2P –d1P º 0 mod P2. (1.46)
Но левая часть последнего сравнения с учетом (1.14), (1.17) и (1.20), а также равенства (1.26) будет
d0P – d2P –d1P = (X + Y) – (Z – Y) – (Z – X) = 2 (X + Y – Z) = 2Kd0d1d2 º 0 mod P2 Þ
Þ K = eP2, что и т.д. (1.47)
в)Модуль K > 3.
Это условие докажем для двух вариантов 2-го случая, а именно:
---для варианта 1, когда (Z,P) =P, а (X,P) = 1 и (Y,P) =1;
---для варианта 2, когда (Z,P) = 1, а (X,P) = P и (Y,P) = 1.
Вариант, когда (Z,P) =1, (X,P) =1 и (Y,P) = P рассматривать не будем ввиду его полной аналогии с вариантом 2.
Доказательство того, что K >3для варианта 1.
Пусть для определенности (для вариантов 1 и 2)
Z > X > Y (1.48)
Из неравенств P(X + Y).> Z – Y > Z – X, и с учетом (1.36) имеем
d0P > d2P >d1P, отсюда d0 > d2 > d1.
Составим алгебраическую сумму (X + Y) – (Z – Y) – (Z – X) = 2(X + Y – Z и умножим правую и левую части полученного равенства на P получим P(X + Y) – P(Z – Y) – P(Z – X) = 2P(X + Y – Z), тогда благодаря равенствам (1.36) и (1.26) имеем d0P - Pd2P - Pd1P = 2PKd0d1d2 Þ d0P = Pd2P + Pd1P + 2PKd0d1d2. Разделим левую часть и последнее слагаемое правой части полученного равенства на d0 получим очевидное неравенство d0P-1 < Pd2P + Pd1P + 2PKd1d2.(в1)
Выразим d0 через числа d1 и d2 для чего из равенства (1.28) вычтем равенство (1.29) и учитывая равенства (1.31) и (1.32) получим a1 - a2 + d2P-1 - d1P-1 = a1 - a2 + (d2 - d1)(d2 + d1)q = Kd0 (d2 - d1), (в2)где q =.d2P-3 + d2P-5d12 + …..+ d22d1P-4 + d1P-3. Обозначим q (для P =5) как qmin = d22 + d12. Из (1.34), (1.35) с учетом условия (1.48) имеем a1 - a2 > 0. В п.1.4.4.(а)найдено, что a1 = e1P +1 и a2 = e2P + 1, тогда a1 - a2 = P(e1 - e2).
Пусть K = 3, тогда из равенства (в2) имеем d0 = (a1 - a2 )/3( d2 - d1) + (d2 + d1)q/3 = P (e1 - e2)/3( d2 - d1) + (d2 + d1)q/3
Будем минимизировать d0, приняв d2 + d1 = 3, q = qmin и (e1 - e2) =3( d2 - d1) и, учитывая, что (d2 - d1, P) = 1 ** получим d0 = P + qmin = P + (d22 + d12). (в3) [** Если(d2 - d1, P) = P, то (X – Y, P) =P, но из (1.36) следует, что (X + Y,P) = P, тогда после сложения X – Y и X + Y получим (2X,P) = P, что противоречит в арианту 1. ]
Неравенство (в1) с учетом (в3) будет
[ P + (d22 + d12)]P-1 < Pd2P + Pd1P + 2P3d1d2 Þ (в4)ÞPP-1 + (P –1)PP-2(d22 + d12) + ….+ (d22 + d12)P-1< Pd2P + Pd1P + 2P3d1d2. Далее при доказательстве будем минимизировать [ P + (d22 + d12)]P-1 отбрасывая часть членов разложения.
Покажем, что 3-и члена разложения бинома (d22 + d12)P-1 > Pd2P + Pd1P. Так (d22 + d12)P-1 = (d22)P- 1 + (P – 1) (d22)P- 2d12 + …..+ (d12)P - 1 > Pd2P + Pd1P.
Одно слагаемое левой части разложения (d22)P- 1 = d2Pd2P – 2 > Pd2P Þ d2P – 2> P, это неравенство справедливо для d2 ³ 2 (d2 не может равняться 1, так как d2 >d1). Пусть d2 =2, тогда 2P – 2 = (1 + 1)P –2 = 1 + P – 2 + (P – 2)(P –3)/2 + ……+ P – 2 + 1 = = P + (P – 2)(P – 3)/2 + ……+ P – 2 > P Þ (P – 2)(P – 3)/2 + ……+ P – 2 > 0, что и подтверждает наше утверждение.
Предпоследние два слагаемых разложения бинома (d22 + d12)P-1 а именно: (P – 1) (d22)P- 2d12 + (d12)P –1 > Pd1P.
Для d1 ³ 2 имеем (d12)P- 1= d1Pd1P – 2> Pd1PÞ d1P – 2 > P,. доказательство аналогичное вышеприведенному для ( d22)P- 1.
Для d1 =1 имеем (P – 1) (d22)P- 2d12 + (d12)P –1 = (P – 1) (d22)P- 2 + 1 > P, это неравенство справедливо, т.к. доказано, что (d22)P- 2 > P.
Таким образом, мы показали, что
(d22 + d12)P-1 > Pd2P + Pd1P.
Теперь покажем, что второе слагаемое разложения [P + (d22 + d12)]P-1, а именно (P –1)PP-2(d22 + d12) > 2P3d1d2 =6Pd1d2
Сократим правую и левую части неравенства на P и, принимая во внимание, что d22 +d12 > d1d2, так как d2 > d1 получим (P – 1)PP – 3 > 6, полученное неравенство справедливо для любых P > 3.
Нами показано, что несмотря на минимизацию d0 и d0P – 1, которая должна усиливать неравенство (в4), получили обратный результат
d0P-1 > Pd2P + Pd1P + 2P3d1d. (в5)