МНОГОКРИТЕРИАЛЬНЫЕ КОНФЛИКТНЫЕ МОДЕЛИ АНАЛИТИЧЕСКИХ ЗАДАЧ
В различных областях практической деятельности частo возникает проблема решения аналитических задач в условиях неопределенности. Более того [академик Моисеев Н.Н.], «Задачи, не содержащие неопределенностей, являются скорее исключением, чем правилом, - адекватное реальности описание проблемы практически всегда содержит различного типа неопределенности».
Принято использовать следующую классификацию неопределенных факторов: неопределенность среды; неопределенность целей; неопределенность поведения активного партнера.
- Неопределенность целей. Имеет основную интерпретацию в виде проблемы многокритериальности. Эффективность принятия любого управленческого решения наиболее адекватно характеризуется векторным показателем.
- Неопределенность среды. Является следствием неполноты априорной и текущей информации об условиях протекания каких-либо процессов, изомерах каких-либо функций и т.д.
- Неопределенность поведения активного партнера. Имеет место, когда при принятии решений сталкиваются интересы различных сторон, преследующих различные цели. При этом результат любого действия каждой из сторон зависит от того, какие действия предпримут другие стороны. Подобные ситуации называются конфликтными.
Эффективность методов решения аналитических задач в значительной степени определяется возможностями учета неопределенных факторов вышеперечисленных типов.
Часть 1. МНОГОКРИТЕРИАЛЬНЫЕ МОДЕЛИ
АНАЛИТИЧЕСКИХ ЗАДАЧ
Основные понятия и определения.
Многие многокритериальные аналитические задачи целесообразно формулировать в виде задач многокритериальной оптимизации.
Задача многокритериальной оптимизации возникает в тех случаях, когда при принятии решений приходится руководствоваться несколькими целями, которые не могут быть отражены единым критерием. Имеет место т.н. неопределенность цели.
Постановку задачи многокритериальной оптимизации будем формулировать в следующем виде:
Определить 
(1)
В (1)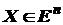 
- n -мерный вектор варьируемых параметров; 
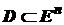- область допустимых значений вектора Х (альтернатив);
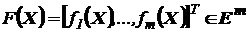- векторная целевая функция.
Множество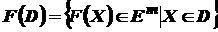 
(2)
называется множеством достижимых векторных оценок (аналогично области значений функций).
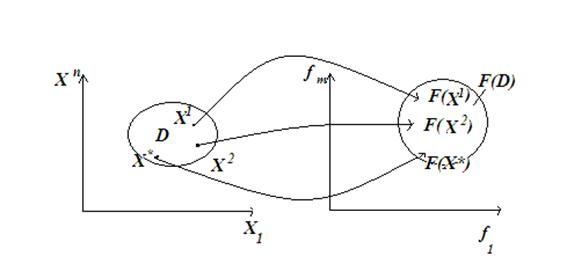
Обычно множество D задается системой неравенств:
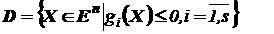(3)
Задача (1), (3) называют конечномерной задачей многокритериальной оптимизации (М0).
Основное отличие рассматриваемой задачи М0от классической задачи нелинейного программирования (НГ) состоит в следующем.
В задаче нелинейного программирования область значений функции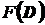 
является отрезком (т.к. 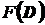- скаляр).
Поэтому решение задачи нелинейного программирования состоит в выборе на отрезке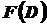 
минимального значения.
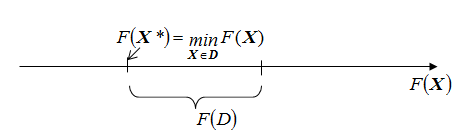
В задаче М0множество 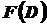является m -мерным. Поэтому элемента 
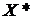, доставляющего минимальные значения всем компонентам векторной целевой функции 
, как правило, не существует.
Вследствие этого в задаче (1), (2) понятие оптимальности требует нового определения.
С этой целью введем понятие бинарного отношения строго предпочтения. (Для определенности будем рассматривать задачу на минимум).
Определение 1. Бинарным отношением 
на множество достижимых векторных оценок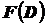 
называется совокупность упорядоченных 
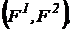где 
Если 
, то говорят, что 
и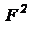 
находятся в отношении , и этот факт записывают так:
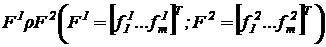
Для описания предпочтений ЛПР широко используются следующие бинарные отношения строгого предпочтения.
Определение 2. Отношение строгого предпочтения Ƥ: F1ƤF2 означает, что объект F1 строго предпочтительнее, чем F2.
Ƥ определяется следующим образом:
F1ƤF2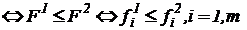 
и 
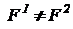(3)
Геометрическая интерпретация (m=2) определения 2
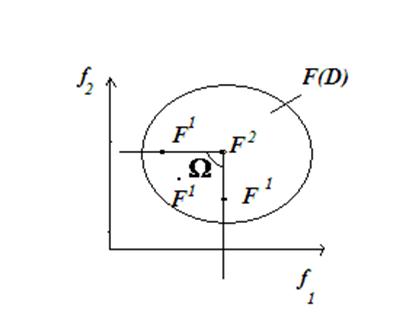
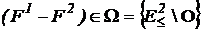
Точка F1 должна находиться внутри конуса Ω или на его гранях.
Определение 3. Элемент F* называется минимальным (недоминируемым) по Ƥ на множестве 
, если в не существует элемента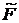 
, строго более предпочтительного, чем 
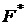, т.е. если 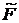Ƥ 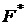не имеет места ни при каких 
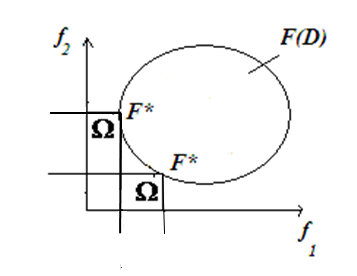
Геометрическая интерпретация определения 3 (m=2)
Определение 4. Векторная оценка 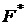минимальная по Ƥ вида (3), называется оптимальной по Парето (эффективной). Множество векторных оценок, минимальных по Ƥ на множестве 
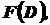называется множеством Парето (эффективным множеством) и обозначается 
Геометрическая интерпретация множества Парето (m=2)
Множество Парето может иметь более сложные конфигурации в зависимости от конфигурации множества допустимых векторных оценок.
Конфигурация множества Парето
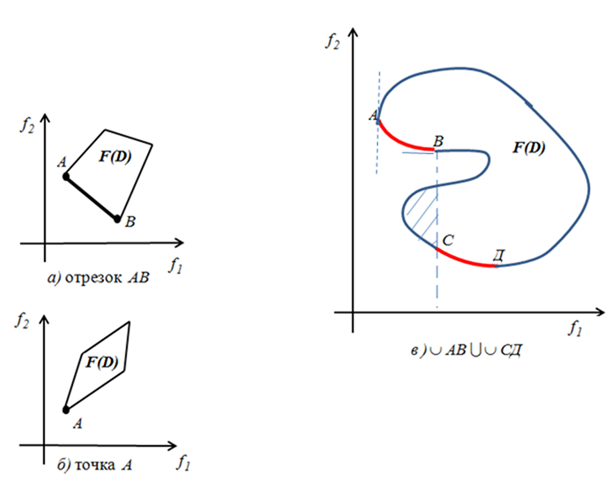
Замечание
Если задача решается на максимум:
Определить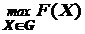 
, то отношение строгого предпочтения Ƥ имеет вид (≥), и множество Парето имеет следующую геометрическую интерпретацию.
Пример 1. (Задача многокритериального линейного программирования)
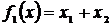
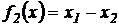
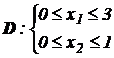
Построить множество Парето для случаев:
а)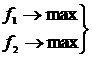 
б)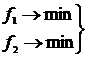 
а) Пространство параметров:
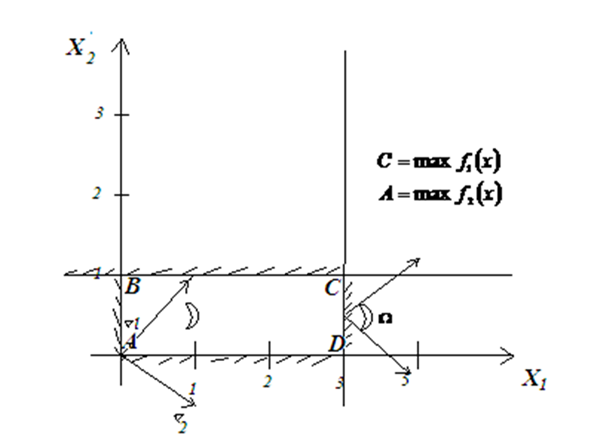
Пространство критериев:
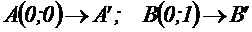
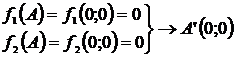
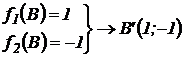
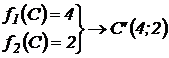
а) Множество Парето: отрезок 
пространстве критериев
б) Множество Парето: отрезок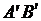 
в пространстве критериев