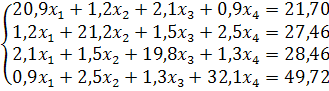Метод квадратных корней.
Метод квадратных корней используется для решения линейной системы:
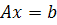
У которой матрица А симметрическая, т.е.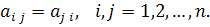 
Он является более экономным и удобным по сравнению с методами решения систем общего вида, рассмотренными ранее.
Решение системы осуществляется в два этапа.
Прямой ход. Представим матрицу А в виде произведения двух взаимно транспонированных треугольных матриц: 
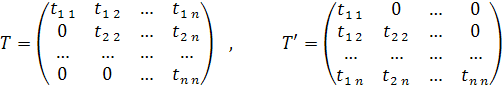
Перемножая матрицы Т' и Т и приравнивая матрице A, получим следующие формулы для определения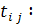 
После того, как матрица Т найдена, систему заменяем двумя эквивалентными ей системами с треугольными матрицами:
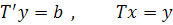
Обратный ход. Записываем в развернутом виде системы:
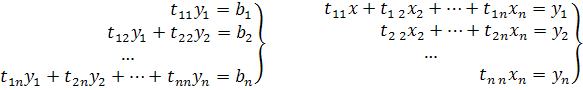
Отсюда последовательно находим:
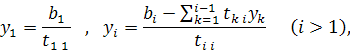
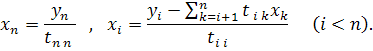
При вычислениях применяется обычный контроль с помощью сумм, причем при составлении суммы учитываются все коэффициенты соответствующей строки.
Заметим, что при действительных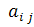 
могут получиться чисто мнимые 
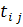. Метод применим и в этом случае.
Метод квадратных корней дает большой выигрыш во времени по сравнению с рассмотренными ранее методами, так как, во-первых, существенно уменьшает число умножений и делений (почти в два раза для больших n), во-вторых, позволяет накапливать сумму произведений без записи промежуточных результатов.
Задание. Решить систему линейных уравнений методом квадратных корней.
Провести эту работу в SMathStudio.
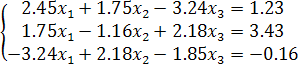
Схема Халецкого.
Рассмотрим систему линейных уравнений, записанную в матричном виде:
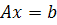
Где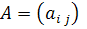 
— квадратная матрица (i, j = 1, 2,..., n) и
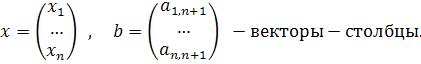
Представим матрицу А в виде произведения А=ВС, где
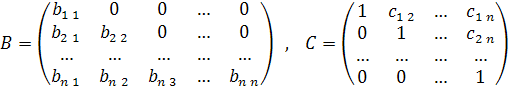
Тогда элементы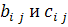 
будут определяться по формулам
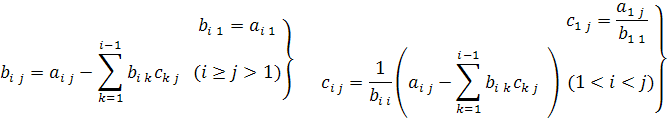
Отсюда искомый вектор х может быть вычислен из цепи уравнений
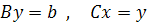
Так как матрицы B и С треугольные, то системы легко решаются, а именно:
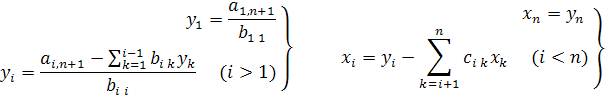
Из формул видно, что числа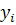 
выгодно вычислять вместе с коэффициентами 
Эта схема вычислений называется схемой Халецкого. В схеме применяется обычный контроль с помощью сумм.
Схема Халецкого удобна для работы на клавишных вычислительных машинах, так как в этом случае операции «накопления» можно проводить без записи промежуточных результатов.
Задание. Решить систему линейных уравнений методом Халецкого.
Провести эту работу в SMathStudio.
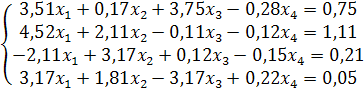
Метод простой итерации
Пусть система линейных уравнений
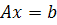
Каким-либо образом приведена к виду
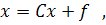
где С – некоторая матрица, а f – вектор-столбец.
Исходя из произвольного вектора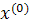 
,
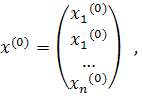
сторим итерационный процесс
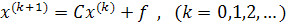
или в развернутой форме
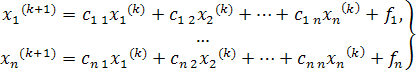
Производя итерации, получим последовательность векторов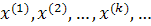 
Доказано, что если элементы матрицы С удовлетворяют одному из условий
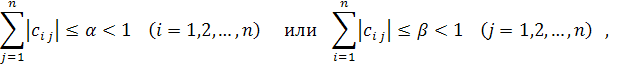
то процесс итерации сходится к точному решению системы х при любом начальном векторе 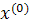, т.е.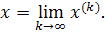 
Таким образом, точное решение системы получается лишь в результате бесконечного процесса и всякий вектор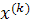 
из полученной последовательности является приближенным решением. Оценка погрешности этого приближенного решения 
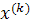дается одной из следующих формул:
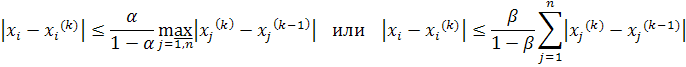
Эти оценки можно усилить соответственно так:
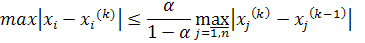
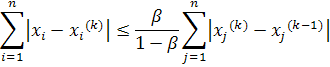
Процесс итераций заканчивают, когда указанные оценки свидетельствуют о достижении заданной точности.
Начальный вектор 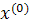может быть выбран, вообще говоря, произвольно. Иногда берут 
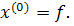Однако наиболее целесообразно в качестве компонент вектора 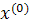взять приближенные значения неизвестных, полученные грубой прикидкой.
Первый способ. Если диагональные элементы матрицы А отлины от нуля, т. е.
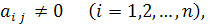
то систему можно записать в виде:
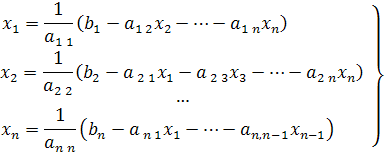
В этом случае элементы матрицы С определяются следующим образом:
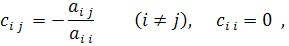
и тогда условия приобретают вид:
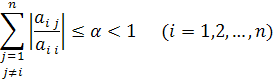
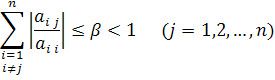
Неравенства будут выполнены, если диагональные элементы матрицы А удовлетворяют условию:
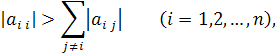
т.е. если модули диагональных коэффициентов для каждого уравнения системы больше суммы модулей всех остальных коэффициентов (не считая свободных членов).
Второй способ покажем на примере.
Вообще говоря, для любой системы с невырожденной матрицей существуют сходящиеся итерационные методы решения, но далеко не всегда они удобны для практических вычислений.
Если метод итераций сходится, он дает следующие преимущества по сравнению с методами, рассмотренными выше.
1) Если итерации сходятся достаточно быстро, т. е. если для решения системы требуется менее n итераций, то получаем выигрыш во времени, так как число арифметических действий, необходимых для одной итерации, пропорционально n2, а общее число арифметических действий в методе Гаусса, например, пропорционально n3.
2) Погрешности округления в методе итераций сказываются значительно меньше, чем в методе Гаусса. Кроме того, метод итераций является самоисправляющимся, т. е. отдельная ошибка, допущенная в вычислениях, не отражается на окончательном результате, так как ошибочное приближение можно рассматривать как новый начальный вектор.
Последнее обстоятельство часто используется для уточнения значений неизвестных, полученных методом Гаусса.
3) Метод итераций становится особенно выгодным при решении систем, у которых значительное число коэффициентов равно нулю. Такие системы появляются, например, при решении уравнений в частных производных.
4) Процесс итераций приводит к выполнению однообразных операций и сравнительно легко программируется на ЭВМ.
Задание. Решить систему линейных уравнений методом простых итераций.
Провести эту работу в SMathStudio.
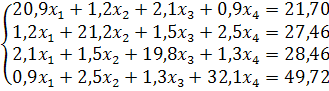
Метод Зейделя.
Метод Зейделя является модификацией метода простой итерации. Он заключается в том, что при вычислении (k + 1)-го приближения неизвестного xi при i>1 используются уже вычисленные ранее (k + 1)-е приближения неизвестных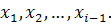 
Таким образом, для системы вычисления по методу Зейделя ведутся по формулам:
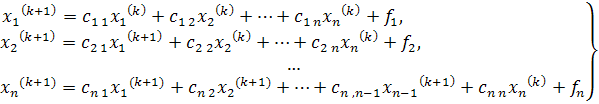
Указанные в методе простой итерации условия сходимости остаются верными и для метода Зейделя. Обычно метод Зейделя дает лучшую сходимость, чем метод простой терации, хотя это бывает не всегда. Кроме того, метод Зейделя может оказаться более удобным при программировании, так как при вычислении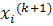 
нет необходимости хранить значения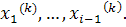 
Задание. Решить систему линейных уравнений методом Зейделя.
Провести эту работу в SMathStudio.
