Задача 1. Решить матричное уравнение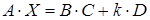 
, где
, 
, 
, 
, 
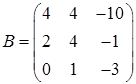Решение:
Убедимся, что 
матрица не является вырожденной, то есть обладает обратной матрицей. Для этого вычислим её определитель:
.
Разложим определитель, например, по элементам второго столбца:
210.
Определитель отличен от нуля, поэтому обратная матрица существует, и мы можем вычислить обратную матрицу по формуле:
.
Вычислим алгебраические дополнения:
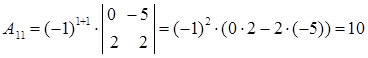
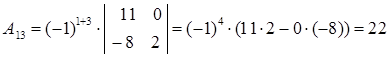
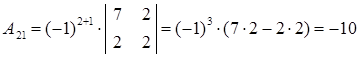
Таким образом, матрица, составленная из алгебраических дополнений, имеет вид:
(
)
Транспонирование матрицы – такое преобразование этой матрицы, при котором ее строки становятся столбцами с теми же номерами. Транспонированная матрица к матрице () будет выглядеть так:
,
тогда
Таким образом, уравнение имеет единственное решение. Выполним преобразование левой части уравнения
, , ,
.
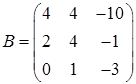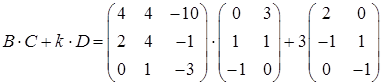Обозначим произведение матриц 
, где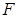 
матрица размерности 
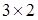элементами 
.
Получим 
. 
.
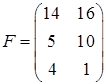Матрица 
и 
.
Исходное уравнение принимает вид
.
Умножим левую и правую части уравнения слева на 
, получаем 
,
.
Задача 2. Решить систему уравнений, используя правило Крамера
Решение:
Вычислим определитель матрицы, составленной из коэффициентов, стоящих при переменных в предложенной системе линейных уравнений:
Его назовем главным определителем, 
. Если главный определитель отличен от нуля, то система имеет единственное решение и найти его можно по правилу Крамера. Для этого заменим в матрице коэффициентов первый столбец на столбец свободных членов, и вычислим определитель такой матрицы:
| 
|
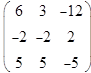
Аналогичным образом, получаем матрицы с замененными вторым и третьим столбцами соответственно, затем, вычислим определители этих матриц.
| 
|
| 
|
Решение системы можно найти таким образом:
Задача 3. Найти косинус угла между векторами 
и площадь параллелограмма, построенного на этих векторах, если известны координаты точек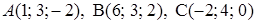 
.
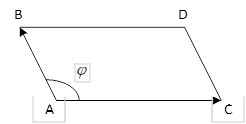
Решение. Найдем координаты векторов 
.
.
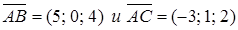Угол между векторами найдем с помощью скалярного произведения векторов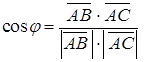 
, где 
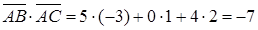и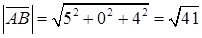 
, 
.
Тогда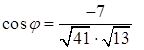 
.
Площадь параллелограмма найдем с помощью модуля векторного произведения векторов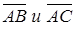 
.
и 
.
Задача 4. Даны координаты вершин пирамиды
. Найти уравнение прямой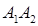 
, уравнение плоскости 
, уравнение высоты, опущенной из вершины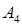 
на грань , вычислить объем пирамиды и расстояние от точки 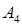до плоскости .
Решение. Найдем координаты векторов
.
Напишем уравнение прямой 
, проходящей через точку 
коллинеарно вектору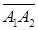 
: 
.
Для того, чтобы написать уравнение плоскости используем уравнение плоскости, проходящей через три заданные точки 
. Раскрывая определитель, получаем уравнение
.
Упростим полученный результат, и находим уравнение плоскости : 
.
Нормальный вектор плоскости 
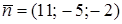коллинеарен высоте пирамиды 
, а значит он является направляющим вектором прямой .
Таким образом, уравнение высоты 
имеет вид
.
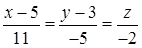Объем пирамиды вычислим используя геометрический смысл смешанного произведения: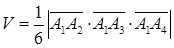 
. Смешанное произведение вычислим как определитель третьего порядка составленный из координат векторов 
. Следовательно, объем пирамиды 
.
Расстояние от точки 
до плоскости можно вычислить, если воспользоваться формулой 
, где 
уравнение некоторой плоскости, а 
точка, не принадлежащая данной плоскости.
Тогда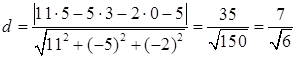 
.
Задача 5. Даны координаты вершин треугольника
.
Найти: а) уравнение высоты 
; б) уравнение медианы 
; в) точку 
пересечения медианы и высоты ; г) уравнение прямой, проходящей через точку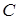 
параллельно стороне 
.
Решение.
а) Найдем координаты вектора 
. Т.к. высота 
, то 
является нормальным вектором для прямой 
, таким образом уравнение высоты имеет вид 
.
Упростим полученное уравнение и получим 
.
б) Вычислим координаты точки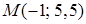 
, как координаты середины отрезка 
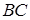. Тогда уравнение прямой, проходящей через две заданные точки имеет вид 
.
Выполним преобразование полученного уравнения
.
в) Вектор 
коллинеарен искомой прямой, а значит служит для этой прямой направляющим вектором. Каноническое уравнение этой прямой имеет вид 
. Выполнив преобразования, получим 
.
Задача 6.
1) Вычислить предел функции 
.
Решение. Используя основные теоремы о пределах видим, что 
и 
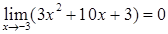. Таким образом выражение 
представляет неопределенность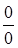 
при 
. Чтобы раскрыть эту неопределенность числитель и знаменатель дроби разложим на множители, найдя корни многочленов. Уравнение 
имеет корни 
. Уравнение 
имеет корни 
. Тогда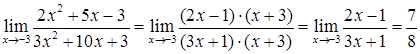 
.
2) Вычислить предел функции 
.
Решение. Так как числитель и знаменатель дроби неограниченно возрастают при неограниченном возрастании аргумента, то выражение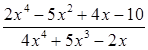 
представляет неопределенность 
. раскроем эту неопределенность поделив числитель и знаменатель дроби на старшую степень переменного т.е. на 
. Получим 
.
3) Вычислить предел функции 
.
Решение. Также как в предыдущем случае, неопределенность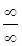 
и раскрываем ее аналогично. 
.
Задача 7. Вычислить производные следующих функций
а) 
; б) 
;
в) 
.
Решение.
а) Вычислим производную функции 
. 
.
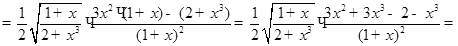
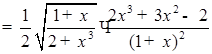б) Вычислим производную функции 
.
.
в) Вычислим производную функции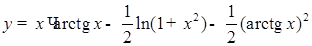 
.
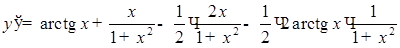
Задача 8. Точка движется прямолинейно по закону 
м. Найти скорость и ускорение в момент 
сек. Определить в какой момент скорость движения точки будет равна нулю.
Решение.
Скорость движения точки выражается равенством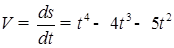 
. В момент 
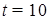сек скорость вычисляется 
.
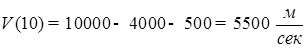Ускорение выражается равенством 
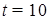. В момент сек. 
.
Скорость движения точки равна нулю если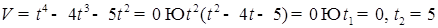 
. Корень уравнения 
не имеет смысла. Таким образом скорость движения точки равна нулю в начальный момент и через 5 сек. после начала движения.