Пример:

Для того чтобы умножить матрицу на число, нужно каждый элемент матрицы умножить на данное число. В данном случае – на тройку.
Сумма (разность) матриц.
Сумма матриц действие несложное.
НЕ ВСЕ МАТРИЦЫМОЖНО СКЛАДЫВАТЬ. Для выполнения сложения (вычитания) матриц, необходимо, чтобы они были ОДИНАКОВЫМИ ПО РАЗМЕРУ.
Например, если дана матрица «два на два», то ее можно складывать только с матрицей «два на два» и никакой другой!
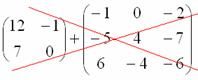
Пример:
Сложить матрицы  и
и 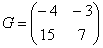
Для того чтобы сложить матрицы, необходимо сложить их соответствующие элементы:
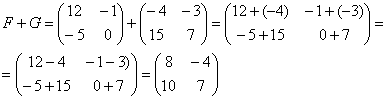
Для разности матриц правило аналогичное, необходимо найти разность соответствующих элементов.
Пример:
Найти разность матриц  ,
, 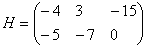
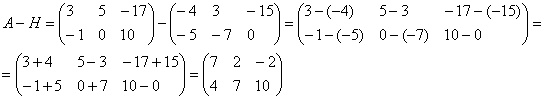
Умножение матриц.
Какие матрицы можно умножать?
Чтобы матрицу  можно было умножить на матрицу
можно было умножить на матрицу  необходимо, чтобы число столбцов матрицы
необходимо, чтобы число столбцов матрицы равнялось числу строк матрицы
равнялось числу строк матрицы .
.
Пример:
Можно ли умножить матрицу  на матрицу
на матрицу  ?
?

 , значит, умножать данные матрицы можно.
, значит, умножать данные матрицы можно.
А вот если матрицы переставить местами, то, в данном случае, умножение уже невозможно!

 , следовательно, выполнить умножение невозможно, и вообще, такая запись не имеет смысла
, следовательно, выполнить умножение невозможно, и вообще, такая запись не имеет смысла

Следует отметить, что в ряде случаев можно умножать матрицы и так, и так.
Например, для матриц,  и
и  возможно как умножение
возможно как умножение  , так и умножение
, так и умножение 
Как умножить матрицы?
Начнем с самого простого:
Пример:
Умножить матрицу  на матрицу
на матрицу 
Сразу привожу формулу для каждого случая:
 – попытайтесь сразу уловить закономерность.
– попытайтесь сразу уловить закономерность.

Пример сложнее:
Умножить матрицу  на матрицу
на матрицу 
Формула: 

В результате получена так называемая нулевая матрица.
Попробуйте самостоятельно выполнить умножение  (правильный ответ
(правильный ответ 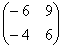 ).
).
|
|
Обратите внимание, что ! Таким образом, переставлять матрицы в произведении нельзя!
! Таким образом, переставлять матрицы в произведении нельзя!
Если в задании предложено умножить матрицу  на матрицу
на матрицу  , то и умножать нужно именно в таком порядке. Ни в коем случае не наоборот.
, то и умножать нужно именно в таком порядке. Ни в коем случае не наоборот.
Переходим к матрицам третьего порядка:
Умножить матрицу  на матрицу
на матрицу 
Формула очень похожа на предыдущие формулы:
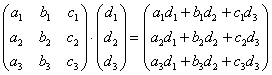

А теперь попробуйте самостоятельно разобраться в умножении следующих матриц:
Умножьте матрицу  на матрицу
на матрицу 
Вот готовое решение, но постарайтесь сначала в него не заглядывать!

1.3. Вычислить определитель матрицы:
а) 
Решение
а) Для вычисления определителя второго порядка воспользуемся правилом, изложенным в учебной литературе:

б) Для вычисления определителя третьего порядка воспользуемся одним из правил, называемым разложением по элементам первой строки:

1.4. Найти обратную матрицу для матрицы второго порядка 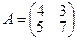
Решение
Для получения обратной матрицы А-1 воспользуемся формулой  , где
, где

Для проверки можно найти произведение матриц А и А-1; должна получиться единичная матрица второго порядка.
Системы линейных уравнений:
1.5. Решить систему уравнений по методу Крамера 
Решение
Для решения задачи нужно вычислить четыре определителя третьего порядка:
· главный определитель, составленный из коэффициентов при неизвестных;
· дополнительный для х, полученный из главного определителя заменой чисел первого столбца на свободные члены;
· дополнительный для у, полученный из главного определителя заменой чисел второго столбца на свободные члены;
· дополнительный для z, полученный из главного определителя заменой чисел третьего столбца на свободные члены;
|
|

Для получения значений неизвестных требуется разделить значения дополнительных определителей на главный определитель.

Решение задачи можно проверить при помощи найденных значений в уравнения системы.