Предпосылки регрессионного анализа. Условия Гаусса-Маркова

Глава 3. Свойства коэффициентов регрессии и проверка гипотез

Случайные составляющие коэффициентов регрессии

Величина Y в модели регрессии Y = a + b× X + e имеет две составляющие: неслучайную (a + b×X) и случайную (e).

Оценки коэффициентов регрессии (a; b)являются линейными функциями Y и теоретически их также можно представить в виде двух составляющих.

Воспользовавшись разложением показателей:

cov(x, y) = cov(x, a + βx + e) = β var(x) + cov(x, e),

,

получим преобразованные соотношения для (a; b):

(3.1)

Таким образом, коэффициенты (a; b) разложены на две составляющие:

неслучайную, равную истинным значениям (a; b) и случайную, зависящую от e.

На практике нельзя разложить коэффициенты регрессии на составляющие, т.к. значения (a; b) или фактические значения e в выборке неизвестны.

Предпосылки регрессионного анализа. Условия Гаусса-Маркова

Линейная регрессионная модель с двумя переменными имеет вид:

y_i = a + b x_i + e _i, (i = 1, n),

где Y –объясняемая переменная, X – объясняющая переменная, e – случайный член.

Для того, чтобы регрессионный анализ, основанный на МНК давал наилучшие из всех возможных результаты, должны выполняться условия Гаусса-Маркова.

1.Математическое ожидание случайного члена в любом наблюдении должно быть равно нулю

M (e_i) = 0, (i = 1, n).

2. Дисперсия случайного члена должна быть постоянной для всех наблюдений

D (e_i) = M (e_i ²) = s ², (i = 1, n).

3. Случайные члены должны быть статистически независимы (некоррелированы) между собой

M (e_ie_j) = 0, (i ¹ j).

4. Объясняющая переменная x_i естьвеличина неслучайная.

При выполнении условий Гаусса-Маркова модель называется классической нормальной линейной регрессионной моделью.

Наряду с условиями Гаусса-Маркова обычно предполагается, что случайный член распределен нормально, т.е. e_i ~ N (0; s ²).

Замечание. Если случайный член имеет нормальное распределение, то требование некоррелированности случайных членов эквивалентно их независимости.

Рассмотрим подробнее условия и предположения, лежащие в основе регрессионного анализа.

Первое условие означает, что случайный член не должен иметь систематического смещения. Если постоянный член включен в уравнение регрессии, то это условие автоматически выполняется.

Второе условие означает, что дисперсия случайного члена в каждом наблюдении имеет только одно значение.

Под дисперсией s ² имеется в виду возможное поведение случайного члена до того, как сделана выборка. Величина s ² неизвестна, и одна из задач регрессионного анализа состоит в её оценке.

Условие независимости дисперсии случайного члена от номера наблюдения называется гомоскедастичностью (что означает одинаковый разброс ). Зависимость дисперсии случайного члена от номера наблюдения называется гетероскедастичностью.

Таким образом,

D (e_i) = s ², (i = 1, n) – гомоскедастичность;

D (e_i) = s_i ², (i = 1, n) – гетероскедастичность.

Характерные диаграммы рассеяния для двух случаев показаны на рис. 9, а и б соответственно.

Рис. 9

Если условие гомоскедастичности не выполняется, то оценки коэффициентов регрессии будут неэффективными, хотя и несмещенными.

Существуют специальные методы диагностирования и устранения гетероскедастичности.

Третье условие указывает на некоррелированность случайных членов для каждых двух соседних наблюдений. Это условие часто нарушается, когда данные являются временными рядами. В случае, когда третье условие не выполняется, говорят об автокорреляции остатков.

Типичный вид данных при наличии автокорреляции показан на рис. 10.

Рис. 10

Если условие независимости случайных членов не выполняется, то оценки коэффициентов регрессии, полученные по МНК, оказываются неэффективными, хотя и несмещенными.

Существуют методы диагностирования и устранения автокорреляции.

Четвертое условие о неслучайностиобъясняющей переменной является особенно важным.

Если это условие нарушается, то оценки коэффициентов регрессии оказываются смещенными и несостоятельными.

Нарушение этого условие может быть связано с ошибками измерения объясняющих переменных или с использованием лаговых переменных.

В регрессионном анализе часто вместо условия о неслучайности объясняющей переменной используется более слабое условие о независимости (некоррелированности) распределений объясняющей переменной и случайного члена. Получаемые при этом оценки коэффициентов регрессии обладают теми же основными свойствами, что и оценки, полученные при использовании условия о неслучайности объясняющей переменной.

Предположение о нормальности распределения случайного члена необходимо для проверки значимости параметров регрессии и для их интервального оценивания.

Теорема Гаусса-Маркова

Теорема Гаусса-Маркова. Если условия 1-4 регрессионного анализа выполняются, то оценки (a, b), сделанные с помощью МНК, являются наилучшими линейными несмещенными оценками, т.е. обладают следующими свойствами:

несмещенности: M (a) = a, M (b) = b, что означает отсутствие систематической ошибки в положении линии регрессии;

эффективности: имеют наименьшую дисперсию в классе всех линейных несмещенных оценок, равную

;

состоятельности: , что означает, что при достаточно большом n оценки (a; b) близки к (a; b).

Для проверки выводов теоремы воспользуемся оценками (a, b) в виде разложения (3.1) и соотношением

.

Пусть x не случайная величина, тогда

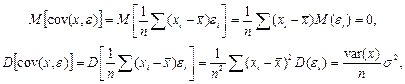
Вычислим математическое ожидание и дисперсию оценок b, a: