Задачи на применение геометрического смысла производной
Задача 1
Прямая y = 5 x − 3 параллельна касательной к графику функции y = x 2 + 2 x − 4. Найдите абсциссу точки касания.
Решение
Прямая параллельная касательной имеет одинаковый с ней угол наклона к оси абсцисс. Т.е., угловой коэффициент касательной (он же тангенс угла наклона) равен 5, как у заданной прямой. С другой стороны, мы знаем, что угловой коэффициент касательной равен производной функции в точке касания. Найдем производную: y '(x) = (x 2 + 2 x − 4)' = 2 x + 2. Составим уравнение, подставив в выражение для производной неизвестную абсциссу точки касания x 0. 2 x 0 + 2 = 5 2 x 0 = 5 − 2 = 3 x 0 = 3/2 = 1,5.
Ответ: 1,5
Задача 2. Найдите угловой коэффициент касательной к кривой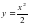 
в точке с абсциссой х 
=8
1) 1 2) 32 3) 16 4) 8
Задача 3
2.Под каким углом к оси Ох наклонена касательная проведённая к кривой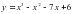 
в точке М (2;-4)?
Задача 4
Прямая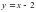 
касается графика функции 
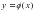в точке 
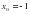.Найдите 
.
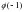Задача 5
.Найдите тангенс угла наклона касательной к положительному направлению оси Ох, проведённой к графику функции у=х(х-2) в точке с абсциссой Хо=1.
Задача 6
При прямолинейном движении тела путь S(t) (в метрах) изменяется по закону S(t)= 
. В какой момент времени ускорение будет равно нулю?
Задача 7
Под каким углом к положительному направлению оси абсцисс наклонена касательная, проведённая в любой точке кривой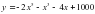 
?
Задача 8
Найдите угловой коэффициент касательной, проведенной к графику функции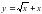 
в точке с абсциссой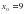 
Задача 9
Дана функция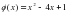 
. Найдите координаты точки, в которой угловой коэффициент касательной к графику функции равен 2.
Задача 10
Угловой коэффициент касательной, проведённой к графику функции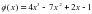 
в точке с положительной абсциссой 
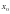,равен 2. Найдите .
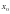Применение производной к решению задач на наибольшее и наименьшее значения.
Заметим, что многие практические задачи приводят к необходимости отыскания наибольшего и наименьшего значения функции не на отрезке, а на интервале или полуинтервале. Фактически к отысканию наибольшего и наименьшего значения функции на отрезке могут привести лишь те задачи, в условии которых содержатся дополнительные ограничения.
Алгоритм нахождения наименьшего и наибольшего значений непрерывной функции y=f(x) на отрезке [a;b]
1. Найти область определения функции
2. Найти производную f’(x)
3. Найти стационарные и критические точки функции, лежащие внутри отрезка [a;b] (y’=0)
4. Вычислить значения функции y=f(x) в точках, отобранных на втором шаге, и в точках a и b; выбрать среди этих значений наименьшее (это будет y наим)
Поясним сказанное примером.
Задача 1. Из квадратного листа жести со стороной 6 дм требуется изготовить открытый сверху резервуар для хранения жидкости, имеющей форму прямоугольного параллелепипеда. Для этого вырезают по углам листа равные квадраты и загибают образовавшиеся края. Какой наибольшей вместимости можно изготовить резервуар?
Если обозначить через х высоту резервуара, выраженную в дециметрах, то решение задачи можно свести к нахождению наибольшего значения функции V(x)=4x(3-x)2 на интервале (0; 3).
Включение дополнительных ограничений в условие задачи, например требования, чтобы высота резервуара была не менее 5 см и не более 20 см, приводит к отысканию наибольшего значения той же функции на отрезке [0,5; 2].
Задача 1. Найти наибольшее и наименьшее значение функции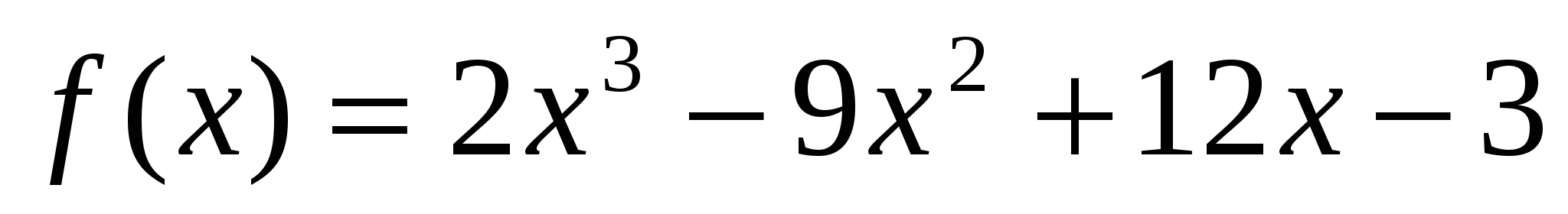 
на отрезке [0; 3].
Решение. Найдем производную данной функции:
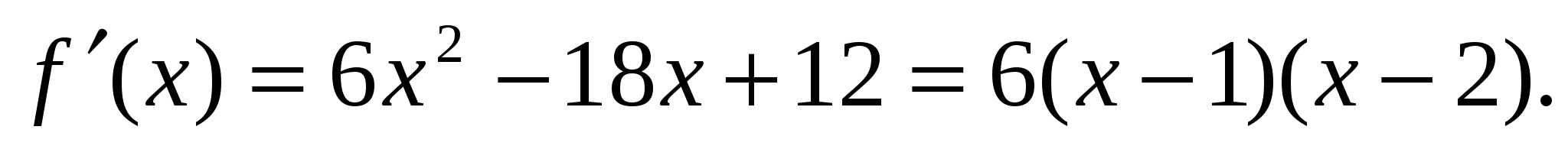Найдем критические точки: х 1=1, х 2=2.
Рассмотрим теперь значения данной функции в точках х 1=0, х 2=1, х 3=2 и
х 4=3: f (0) = – 3, f (1) = 2, f (2) = 1, f (3) = 6. Далее из конечного множества чисел { – 3, 1, 2, 6} следует выбрать наименьшее, т.е. – 3, оно и будет наименьшим значение значением данной функции f наим = f (0) = – 3; взяв наибольшее из чисел, т.е. 6, мы найдем наибольшее значение функции: f наиб = f (3) = 6.
Задача 2. Найти наибольшее и наименьшее значения функции:
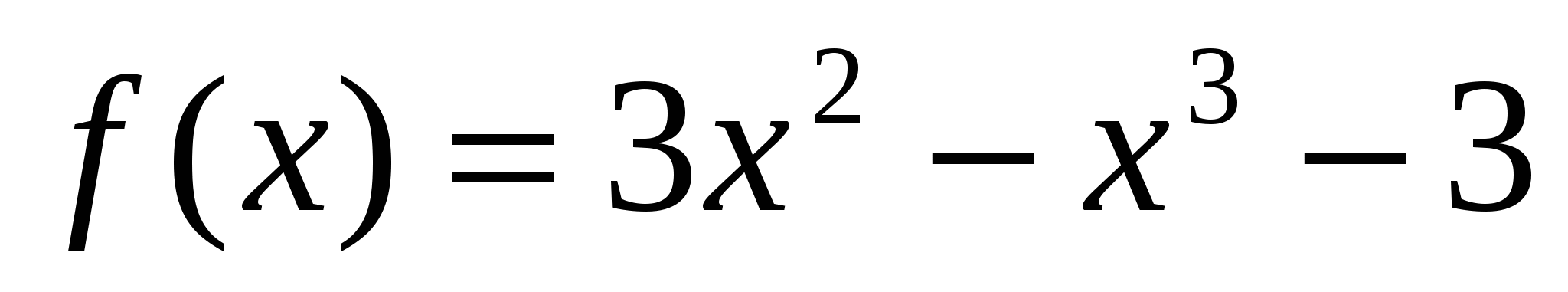на отрезке: а) [-1; 1]; б) [0; 3]; в) [3; 4];
Задача 3.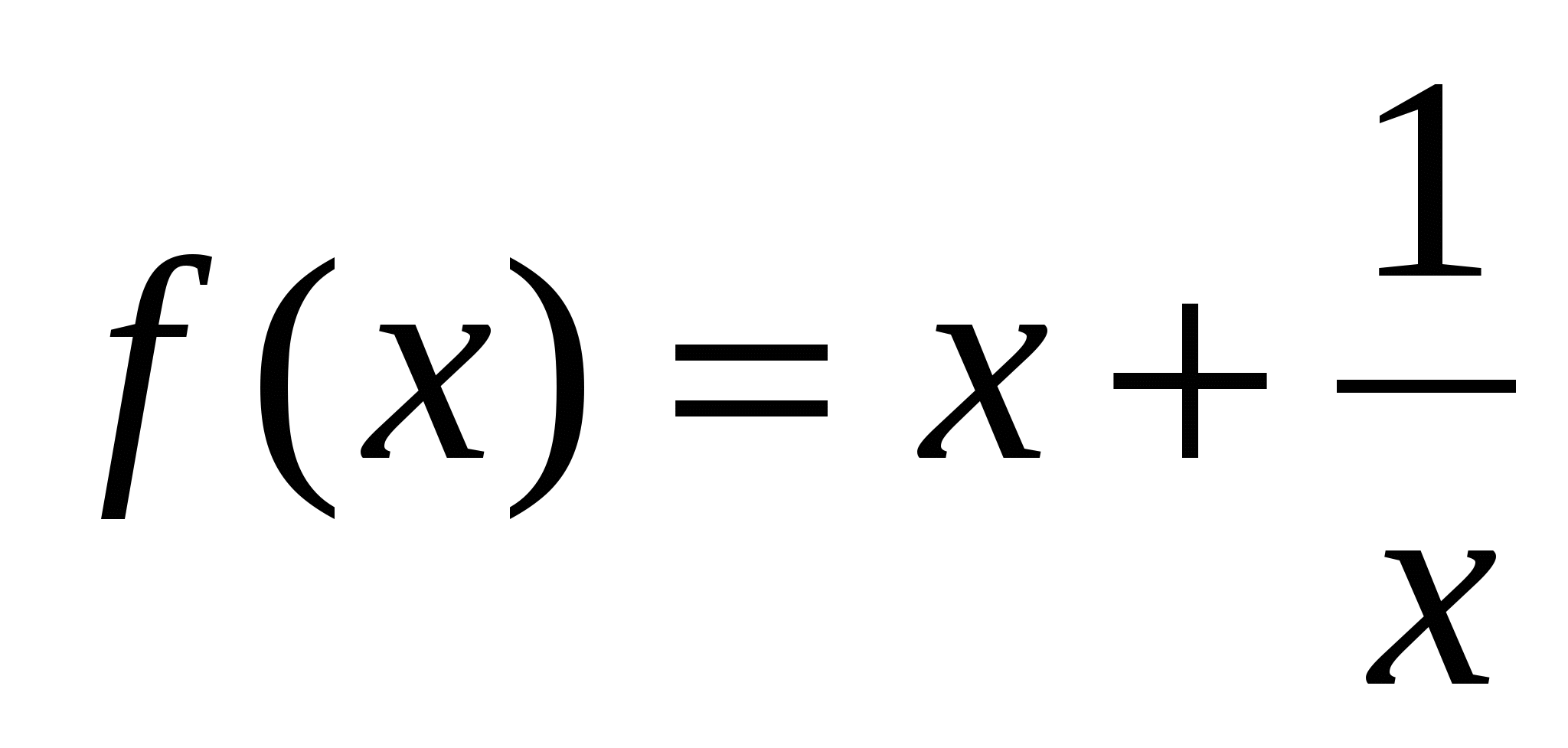 
на отрезке 
;
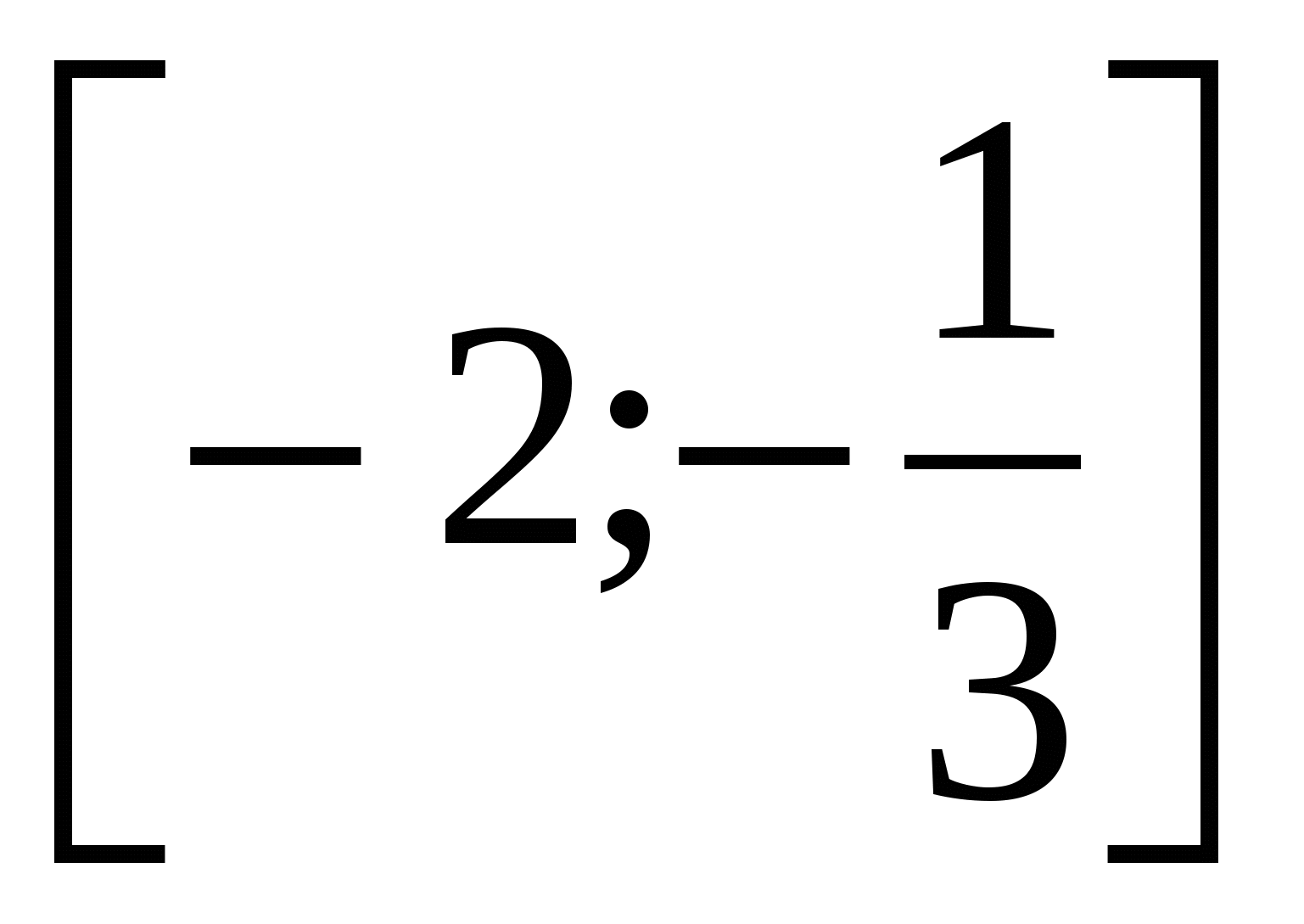Задача 4.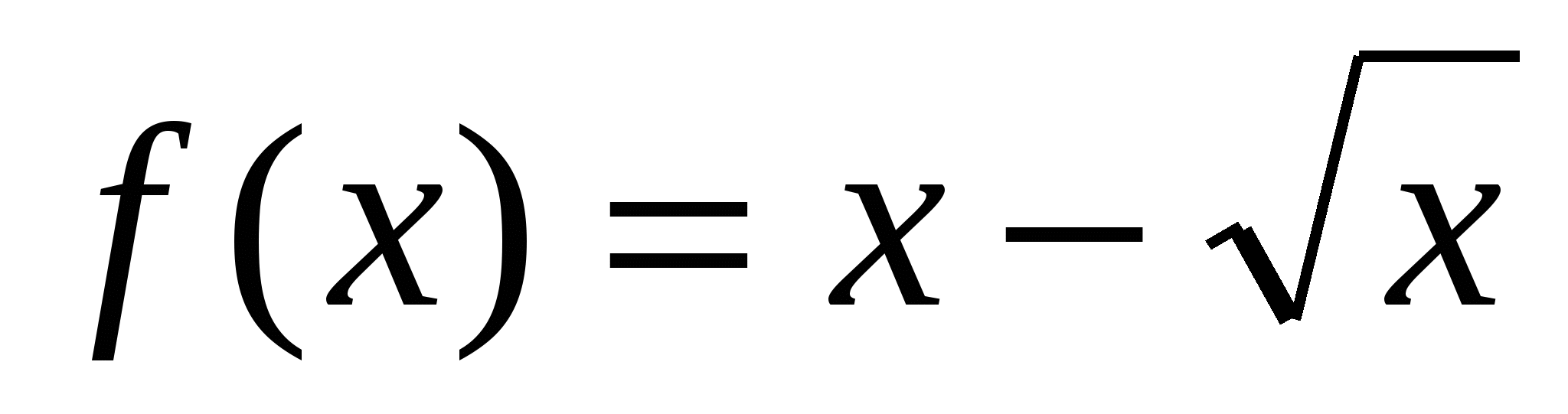 
на отрезке [0; 4];
Задача 5.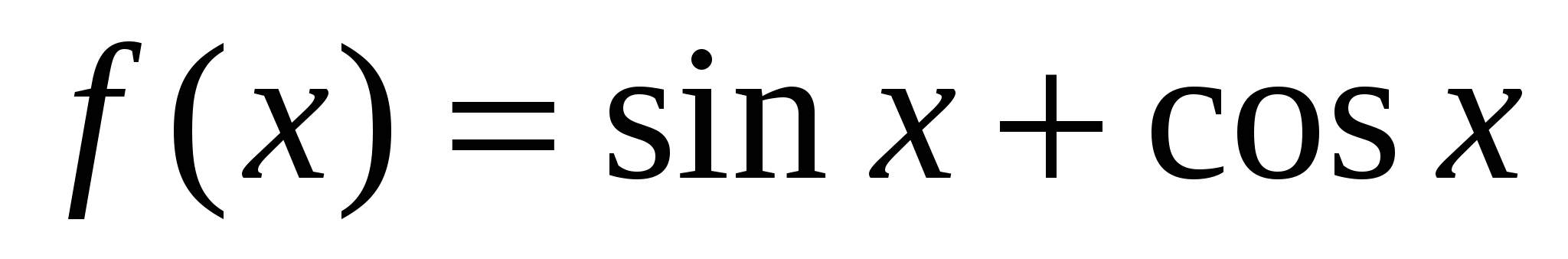 
на отрезке: а) 
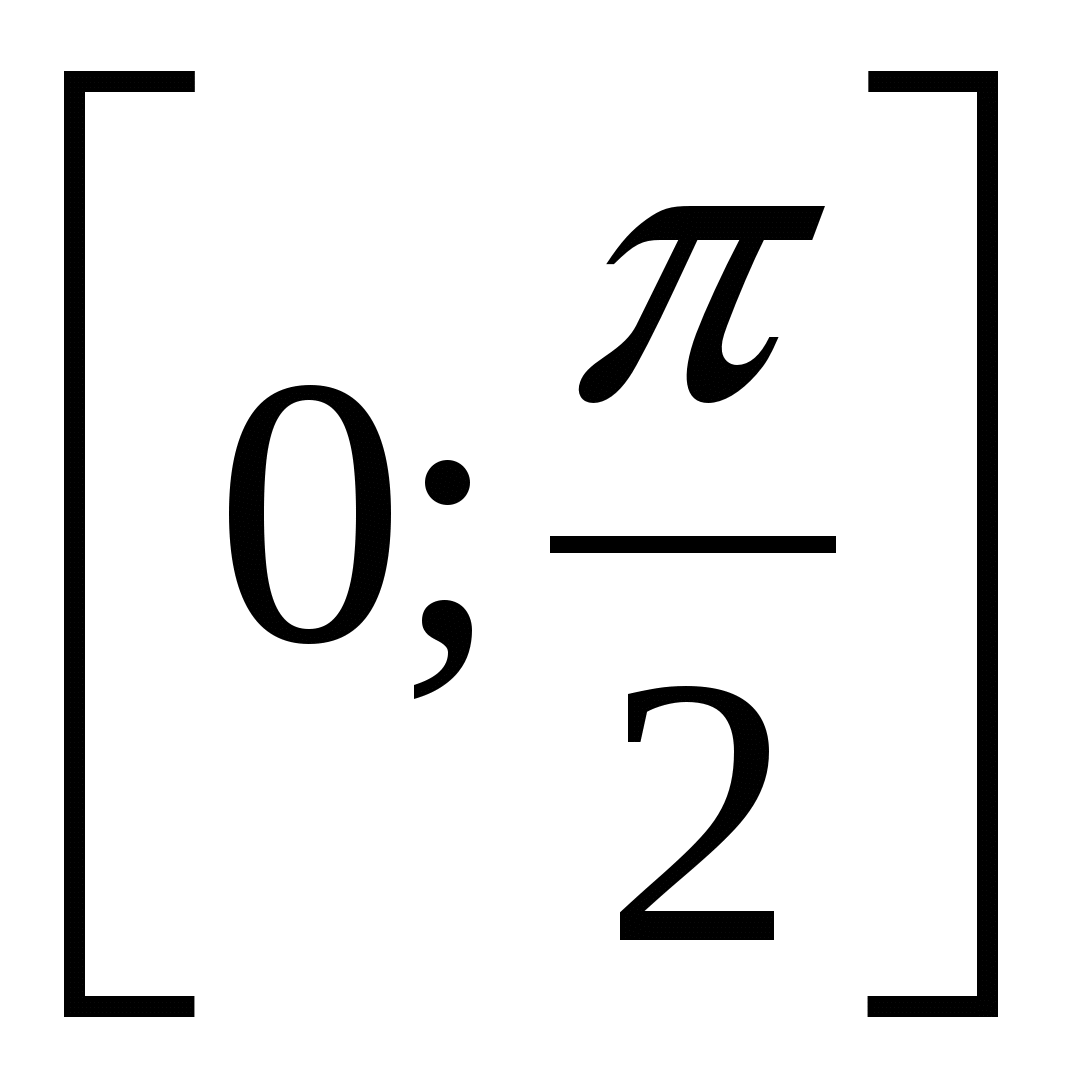; б)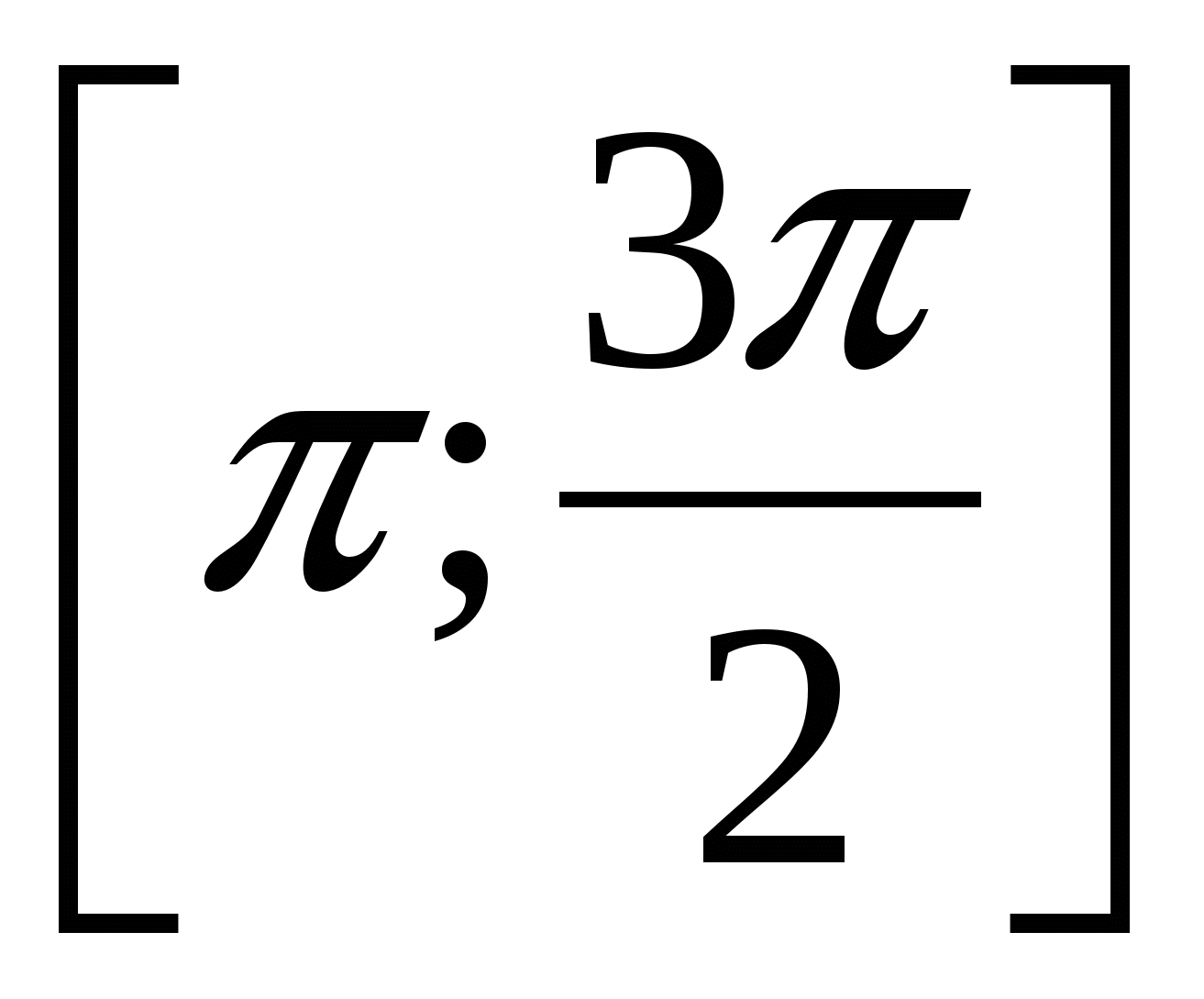 
.
Задача 6.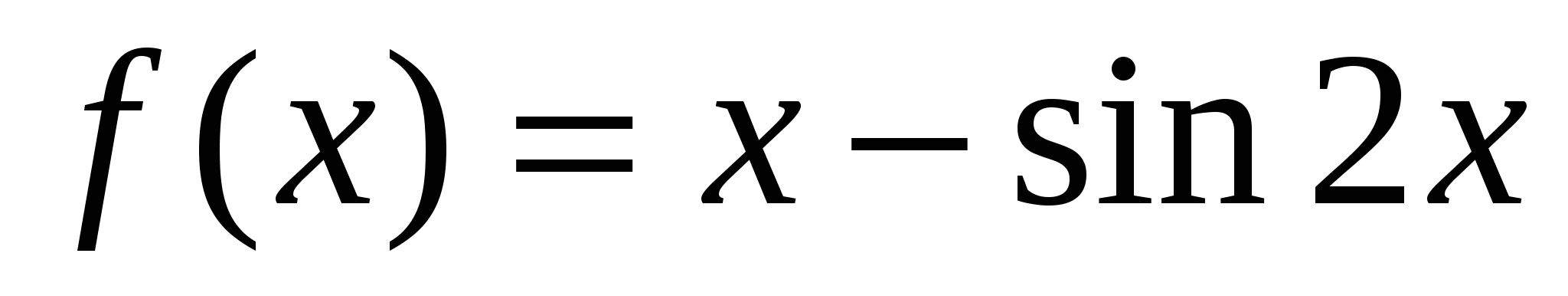 
на отрезке: а) 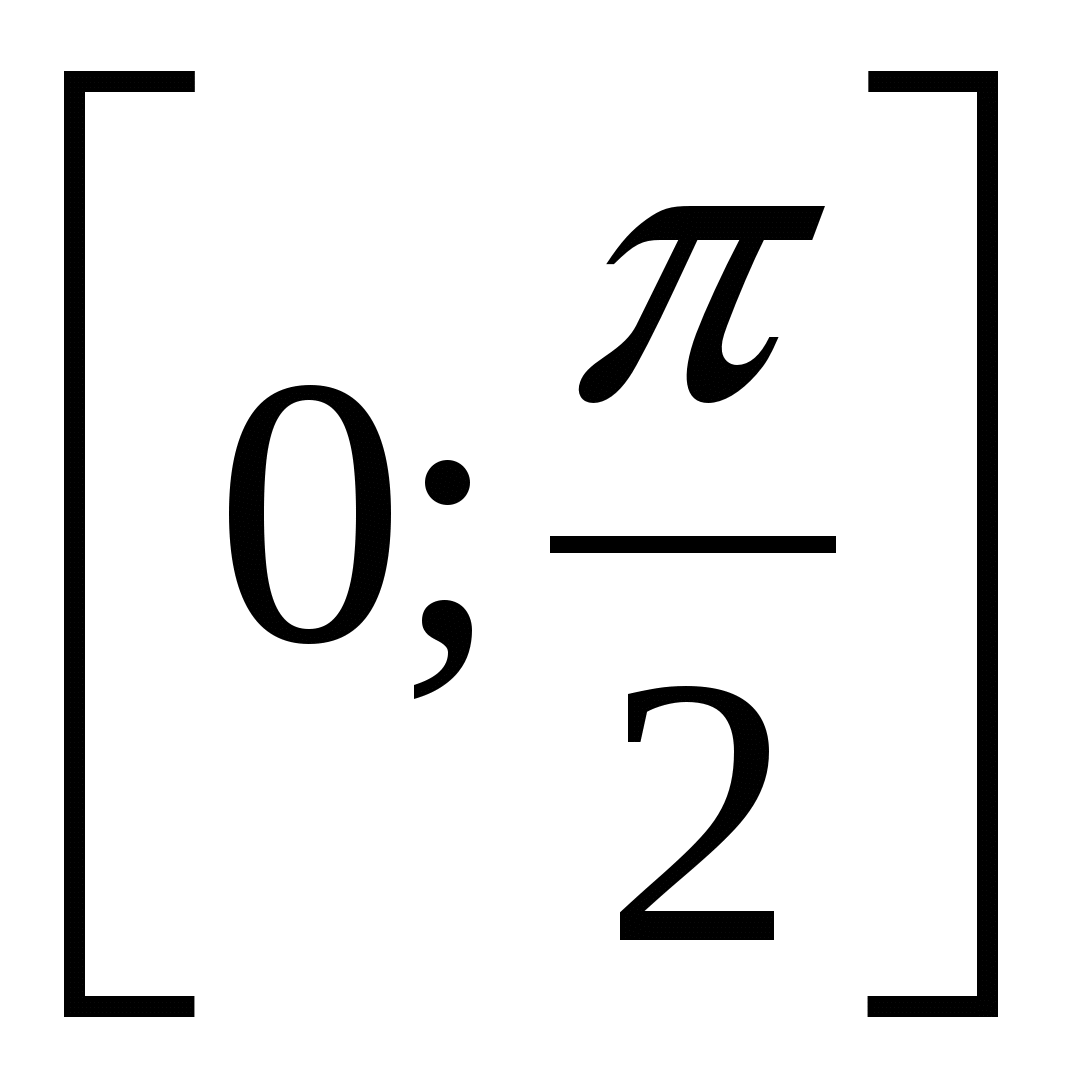; б)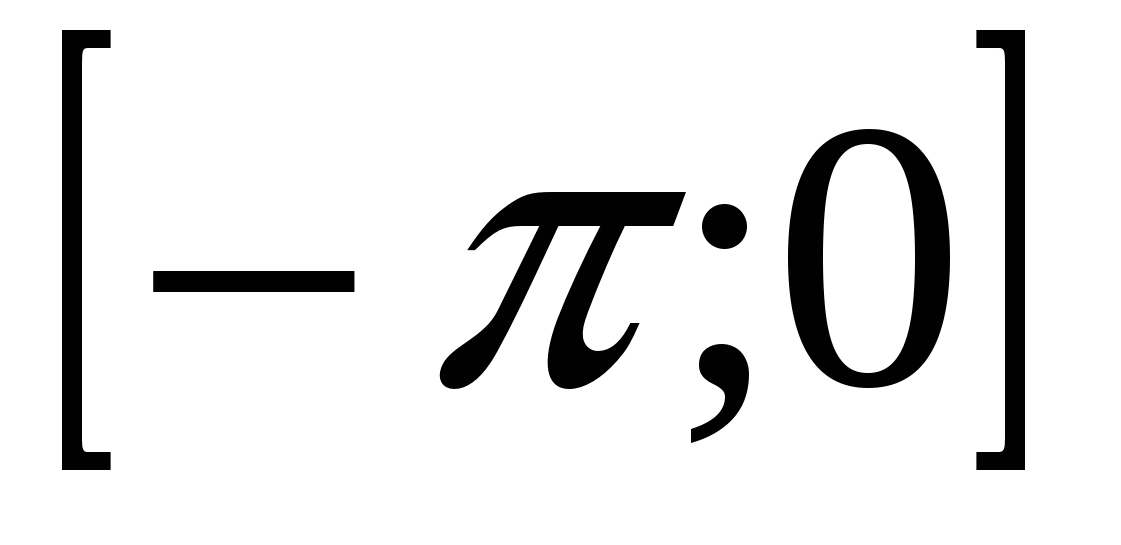 
.
Задача 7. Имеется 40 м проволочной сетки. Требуется оградить три стороны прямоугольного участка земли, примыкающего четвертой стороной к стене здания. Каковы должны быть размеры участка, чтобы его площадь была наибольшей, если длина стены здания равна: а) 30м; б) 10м?
Если обозначить через х м длину стороны участка, прилегающей к стене здания, то задача сведется к отысканию наибольшего значения функции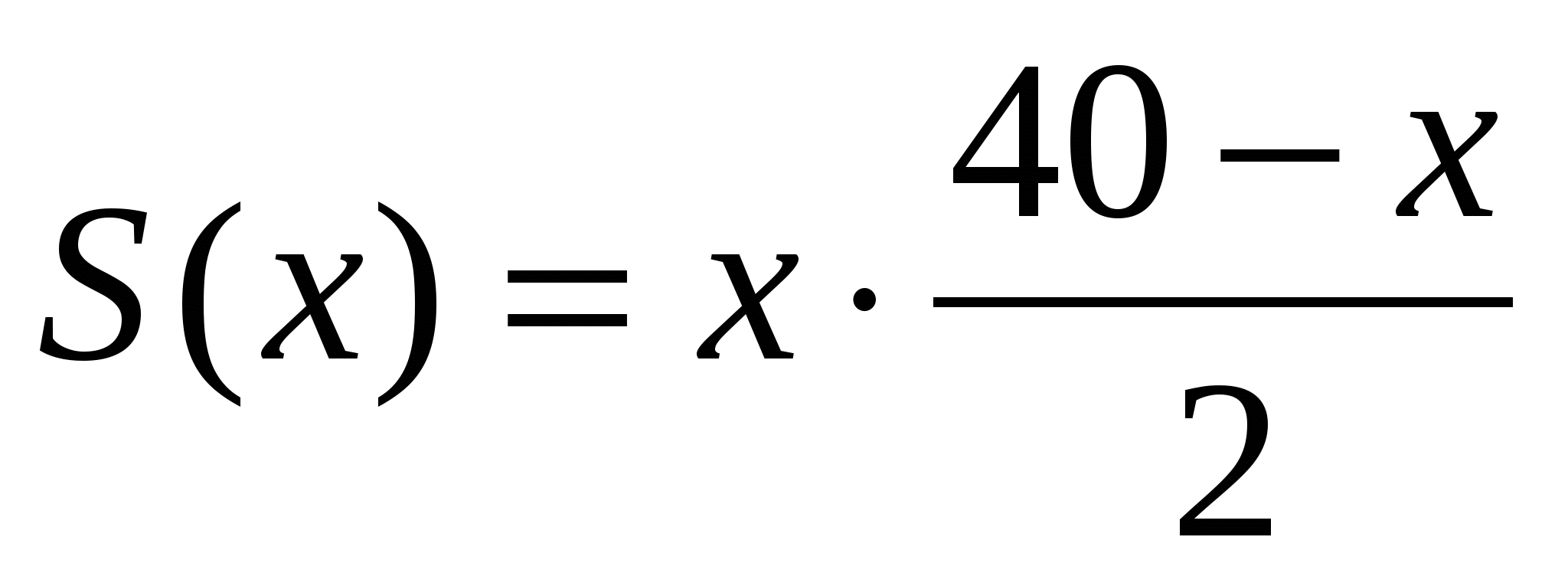 
в промежутке: а) (0; 30]; б) (0; 10]. В первом случае функция достигает наибольшего значения в критической точке х =20, во втором – на конце промежутка, при х =10.
Задача 8. Через диагональ основания правильной четырехугольной призмы проведена плоскость, пересекающая оба основания. Высота призмы равна 4 см, а длина диагонали основания в k раз болше этой высоты. Найти наибольшее значение площади сечения при условии: а) k = 3; б) k = 4,5.
Если обозначить В1К=х см (рис.69), то задача сведется к отысканию наибольшего значения функции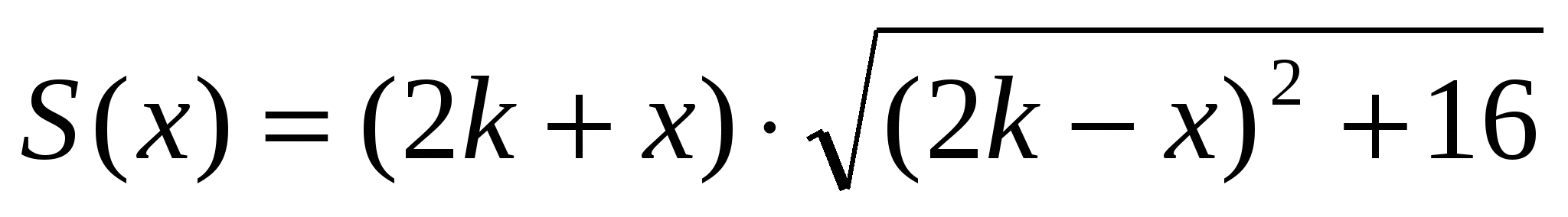 
на отрезке [0; 2 k ]/ Учитывая, что эта функция положительна на рассматриваемом отрезке, отыскание ее критических точек можно свести к отысканию критических точек функции 
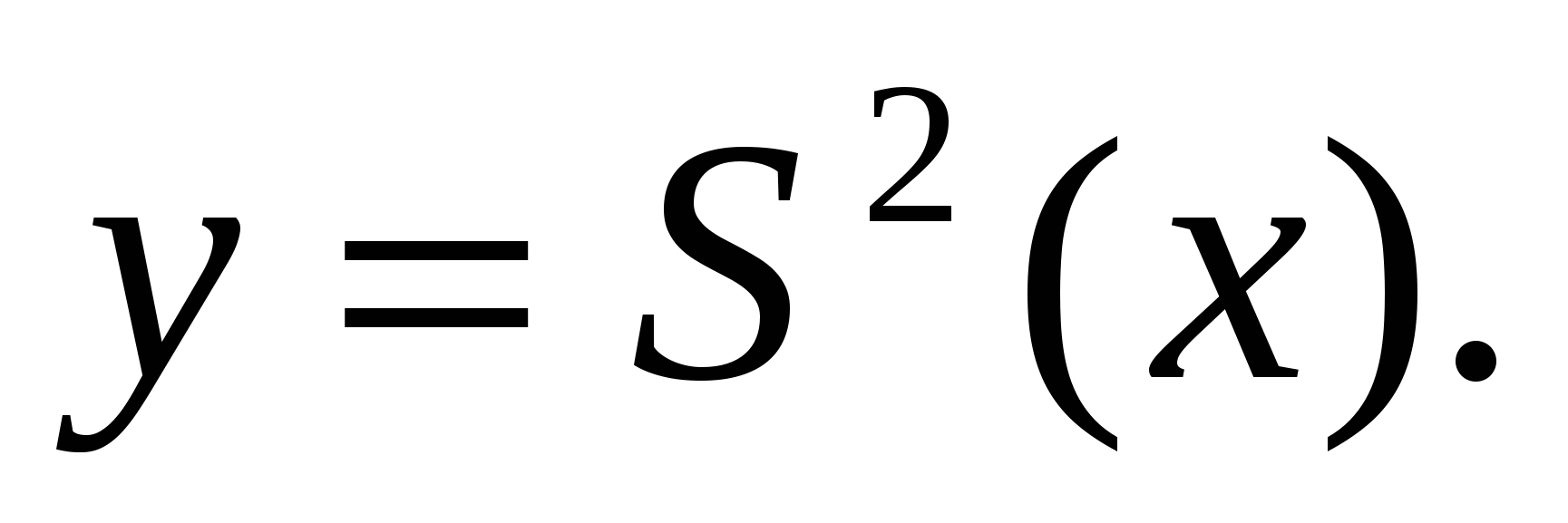В результате получаем, что в заданном промежутке содержатся две критические точки, причем при k = 3 наибольшее значение достигается на конце отрезка, в точке х =6 (т.е. наибольшую площадь имеет диагональное сечение), а при k = 4,5 – в критической точке х =1.
Памятка
Для учащихся, решающих познавательные задачи
1. Внимательно прочтите условие задачи и запомните вопросы к ней.
2. Начните обдумывать данные условия (слово за словом, строку за строкой) и определите, что они дают для ответа на вопрос.
3. Подумайте, не противоречат ли друг другу данные в условии задачи, не помогают ли одни данные понять значение других данных того же условия.
4. Если в условии не хватает каких-либо данных, вспомните, что вы знаете по теме задачи, и подумайте, что из этих знаний может помочь решению.
5. Обязательно докажите свое решение. Если из условия задачи следует несколько выводов, каждый из них надо доказать. Проверьте, готовы ли вы ясно и убедительно изложить доказательство.
6. Проверьте, является ли ваше решение ответом по существу вопроса задачи. Полон ли ваш ответ? Нет ли лишнего, не относящегося к вопросу задачи?
7. Еще раз проверьте, нет ли в условии задачи данных, противоречащих вашему решению. Все ли данные вы учли?
8. Проверьте, все ли возможные выводы по существу вопроса задачи вы сделали и доказали.
Заключение:
Производная успешно применяется при решении различных прикладных задач в науке, технике и жизни
Как видно из вышеперечисленного применение производной функции весьма многообразно и не только при изучении математики, но и других дисциплин. Поэтому можно сделать вывод, что изучение темы: «Производная функции» будет иметь своё применение в других темах и предметах.
Мы убедились в важности изучения темы "Производная", ее роли в исследовании процессов науки и техники, в возможности конструирования по реальным событиям математические модели, и решать важные задачи.
В заключении я хочу вам прочитать стихотворение:
“Музыка может возвышать или умиротворять душу,
Живопись – радовать глаз,
Поэзия – пробуждать чувства,
Философия – удовлетворять потребности разума,
Инженерное дело – совершенствовать материальную сторону жизни людей,
А математика способна достичь всех этих целей”.
Так сказал американский математик Морис Клайн.
Литература:
1. Богомолов Н.В., Самойленко И.И. Математика. - М.: Юрайт, 2015.
2. Григорьев В.П., Дубинский Ю.А, Элементы высшей математики. - М.: Академия, 2014.
3. Баврин И.И. Основы высшей математики. - М.: Высшая школа, 2013.
4. Богомолов Н.В. Практические занятия по математике. - М.: Высшая школа, 2013.
5. Богомолов Н.В. Сборник задач по математике. - М.: Дрофа, 2013.
6. Рыбников К.А. История математики, «Издательство Московского университета», М, 1960.
7. Виноградов Ю.Н., Гомола А.И., Потапов В.И., Соколова Е.В. – М.: Издательский центр «Академия», 2010
8. Башмаков М.И. Математика: алгебра и начала математического анализа, геометрия. – М.: Издательский центр «Академия», 2016
Периодические источники: Газеты и журналы: «Математика», «Открытый урок»
Использование ресурсов сети Интернет, электронных библиотек:
https://ru.wikipedia.org/wiki
https://dic.academic.ru/