Задание 1
Проверить совместность системы уравнений и в случае совместности решить ее:
а) по формулам Крамера;
б) с помощью обратной матрицы (матричным методом);
в) методом Гаусса.
5. 
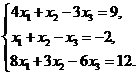
Чтобы проверить, совместна ли система, найдём определитель матрицы системы:
Т.к. этот определитель не равен 0, то система совместна. Решим её:
Решим её:
а)по формулам Крамера. Для этого запишем матрицу данной системы и найдём её определитель D. Затем, последовательно заменяя соответствующий столбец столбцом свободных членов и находим соответственно определителиD1,D2,D3.После этого, используя формулы Крамера находим 
, , . Вычислим необходимые определители:
Тогда получаем по формулам Крамера:
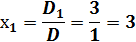
б) с помощью обратной матрицы (матричным методом):
Найдём матрицу, обратную матрице заданной системы. Для этого воспользуемся формулой:
где Аmnалгебраическое дополнение элемента матрицы системы, т.е. произведение минора второго порядка, полученного вычёркиванием m-й строки и n-го столбца в определителе матрицы системы А, на (-1)m+n. Найдём элементы Аmn:
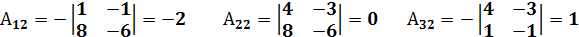
X=А-1 
В, 
- матрица-столбец свободных членов.
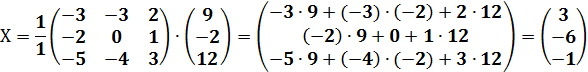
в) методом Гаусса:
Выполним элементарные преобразования и приведём расширенную матрицу системы к «ступенчатому» виду:
Откуда
Ответ:
Задание 2
По координатам точек А, В и С для указанных векторов найти:
а) модуль вектора 
; б) скалярное произведение векторов и 
; в) проекцию вектора 
на вектор ; г) координаты точки M, делящей отрезок l в отношении 
: 
, 
и 
, 
, 
, 
, 
, 
, .
Решение
Найдем векторы:
,
1) 
.
2) 
.
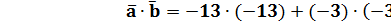3) Проекция вектора на вектор равна:
.
Тогда 
.
4) Координаты точки М, делящей отрезок l в отношении 
, находятся по формулам:
,
,
.
Значит, M(
; 
; ).
Задание 3
Даны векторы 
. Показать, что векторы 
образуют базис четырехмерного пространства, найти координаты вектора в этом базисе: 
(5;1;-7;2), (2;-3;-1;-9), (-7;-1;1;-2), (3;4;-5;-6), (59;20;-38;-53).
Решение
Векторы (5;1;-7;2), (2;-3;-1;-9), (-7;-1;1;-2), (3;4;-5;-6)образуют базис, так как 
.
Обозначим координаты вектора в новом базисе 
. Тогда в новом базисе будем иметь: 
.
, получим систему уравнений:
.
Вычислим:
- система совместна;
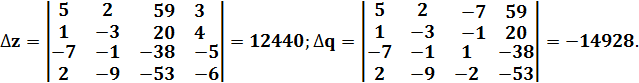
Найдем x, y, z, q по формулам Крамера:
;
.
Итак, получаем ответ 
.
Задание 4
Даны вершины 
, 
и 
треугольника.
Найти: 1) длину стороны АВ; 2) внутренний угол А в радианах с точностью до 0,001; 3) уравнение высоты, проведенной через вершину С; 4) уравнение медианы проведенной через вершину С; 5) точку пересечения высот треугольника; 6) длину высоты, опущенной из вершины С; 7) систему линейных неравенств, определяющих внутреннюю область треугольника АВС. Сделать чертеж.
Решение
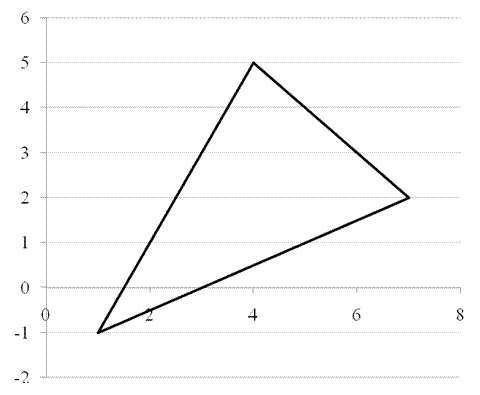
Рисунок 1
;
; 
.
По теореме косинусов: 
.
Тогда угол A равен 36,9 
.
3) Уравнение стороны АВ запишем, используя уравнение прямой, проходящей через точки А(), В():
.
Тогда 
.
Уравнение прямой АВ примет вид: 
.
Так как СН перпендикулярна АВ, то 
.
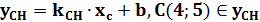
Тогда 
.
4) Так как CM – медиана, то точка M – середина AB. Значит, , или 
.
Уравнение прямой CM примет вид: 
.
5) Уравнение стороны АС запишем, используя уравнение прямой, проходящей через точки А(), С(
):
.
Тогда .
Уравнение прямой АС примет вид: 
.
Так как BK перпендикулярна АC, то 
.
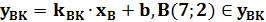
Тогда 
.
Прямые BK и CH пересекаются в точке O, найдем ее координаты. Для этого решим систему:
.
Тогда O(
) – точка пересечения высот исходного треугольника.
6) Прямые AB и CH пересекаются в точке H, найдем ее координаты. Для этого решим систему:
.
Тогда H(
). Значит, 
.
7) Уравнение стороны BС запишем, используя уравнение прямой, проходящей через точки B(), С():
.
Тогда .
Уравнение прямой BС примет вид: 
.
Cистемa линейных неравенств, определяющих внутреннюю область треугольника АВС, примет вид:
.
Задание 5
а) Составить уравнение плоскости, проходящей через точки А(1;1;0), В(2;-1;-1) перпендикулярно к плоскости 
.
б) Найти координаты точки, симметричной точке М(2;8;0) относительно прямой 
.
Решение
а) 
, 
; .
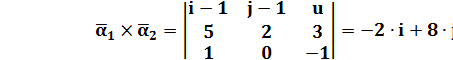Искомое уравнение плоскости: 
.
б) Найдем уравнение перпендикуляра и его основание, опущенного на заданную прямую и проходящего через точку М(2;8;0). Для этого решим систему уравнений:
.
Координаты основанияОравны (-2;-2;2), и эта точка является серединой отрезка 
, где 
- искомая точка. Тогда 
. Значит, 
.
Задание 6
Найти пределы:
а) 
;
б) 
;
в) 
;
г) 
.
Задание 7
а) Найти производные указанных функций:
;
б) Найти производную неявно заданной функции:
.
в) Найти производные функций, используя логарифмическую производную:
ln 
.
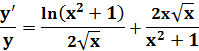
Задание 8
Исследовать функцию и построить ее график: 
.
Решение
1. Область определения функции 
;
2. Функция четная; непериодическая;
3. График функции пересекает ось ординат в точке (0;1).
4. Производная функции равна 
.
Так как 
при 
, то функция убывает;так как при , то функция возрастает. Значит, в точке функция достигает своего минимума 
.
5. Производная 2-го порядка равна 
.
При 
, функция вогнутая;
при 
, функция выпуклая.
6. Функция имеет вертикальные асимптоты 
. Так как 
, то горизонтальная асимптота .
7. Инструментами программы MathCad построим график заданной функции:
Задание 9
В треугольник с основанием b и высотой h вписать прямоугольник с наибольшей площадью.
Решение
Рисунок 1
Пусть BP=h, AC=b, LM=x, LK=OP=y. Тогда 
.
Площадь вписанного прямоугольника равна: 
.
Тогда 
. Если 
, то 
.
При 
, тогда функция 
возрастает;
при 
– функция 
убывает.
Следовательно, в точке 
функция площади вписанного прямоугольника достигает своего максимума.
Отсюда , 
.
Если длина и ширина вписанного прямоугольника будут равны и ,топрямоугольник будет обладать наибольшей площадью.
Ответ: и .
СПИСОК ИСПОЛЬЗОВАННЫХ ИСТОЧНИКОВ
1 Бортаковский, А.С. Аналитическая геометрия в примерах и задачах: Учеб.пособие/А.С.Бортаковский, А.В.Пантелеев. – М.: Высш.шк., 2005. – 466 с.: ил. – (Серия «Прикладная математика»).
2 Выгодский, М.Я. Справочник по высшей математике. – М., 1977, 872 с. с илл.
3 Гусак, А.А. Справочное пособие по решению задач: аналитическая геометрия и линейная алгебра. – Мн.: ТетраСистемс, 1998.
4 Гусак, А.А. Справочное пособие по высшей математике /А.А.Гусак, Г.М.Гусак, Е.А.Бричикова – 4-е изд. Стереотип. – Мн.: ТетраСистемс, 2002.
5 Кузнецов, А.В., Кузнецова, Д.С., Шилкина. Е.И. и др. Сборник задач и упражнений по высшей математике. Общий курс. Учебное пособие. Мн., Выш. шк., 1994 г. 284 с.
6 Руководство к решению задач по высшей математике: Учеб.пособие. В 2ч. Ч.1,2 /Г.И.Гурский, В.П.Домашов, В.К.Кравцов, А.П.Сильванович; Под общ.ред. Г.И.Гурского – Мн.: Высш.шк., 1990.
7 Сочнев, С.В. Элементы высшей математики. Сб. заданий для практ. занятий: Учеб.пособие / С.В.Сочнев – Мн.: Выш.шк., 2003.