Рекуррентные соотношения
Решение многих комбинаторных задач зачастую осуществляется путем сведения данной задачи к задаче, касающейся меньшего числа предметов. Метод сведения к аналогичной задаче для меньшего числа предметов называется методом рекуррентных соотношений. Рекуррентными соотношениями будем называть такие соотношения, которые позволяют получить информацию об 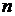 предметах, используя информацию об
предметах, используя информацию об 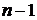 (
(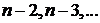 ) предметах.
) предметах.
Например, из комбинаторики известно, что 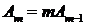 , т.е. число перестановок из
, т.е. число перестановок из 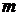 элементов можно вычислить, зная число перестановок из
элементов можно вычислить, зная число перестановок из 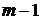 элементов. Таким образом, зная начальное условие
элементов. Таким образом, зная начальное условие 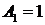 , можно найти
, можно найти 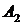 ,
, 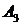 , …,
, …, 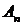 , … рекуррентным способом.
, … рекуррентным способом.
Аналогично, формула 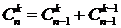 дает рекуррентное соотношение для числа сочетаний. Таким образом, зная, что
дает рекуррентное соотношение для числа сочетаний. Таким образом, зная, что 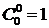 и
и 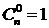 и
и 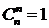 , можно получить все значения
, можно получить все значения 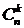 с помощью последовательных вычислений:
с помощью последовательных вычислений:
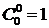
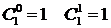
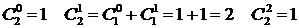
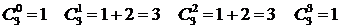
…
Действуя таким образом, мы получили треугольник Паскаля.
Одной из наиболее известных задач, связанных с рекуррентными соотношениями, является задача о кроликах итальянского купца Фибоначчи. Задача состоит в следующем: пара кроликов приносит раз в месяц приплод из двух крольчат, причем, новорожденные крольчата через два месяца после рождения уже приносят приплод. Сколько кроликов получится через год, если в начале было два кролика?
Для решения задачи проведем простейшие рассуждения, обозначая число пар кроликов в начале 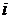 -го масяца через
-го масяца через 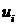 :
:
· 1 января мы имели 1 пару новорожденных кроликов ( );
);
· 1 февраля мы все еще имеем одну пару кроликов (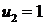 ), которые, впрочем, уже перестали быть новорожденными.
), которые, впрочем, уже перестали быть новорожденными.
· 1 марта получим первый приплод, то есть, две пары кроликов (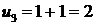 ), одна из которых новорожденная.
), одна из которых новорожденная.
· 1 апреля одна из пар даст приплод, и мы получим три пары кроликов (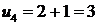 ), одна из которых новорожденная.
), одна из которых новорожденная.
· 1 мая две пары дадут приплод, и мы получим 5 пар кроликов (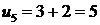 ), 2 из которых новорожденные.
), 2 из которых новорожденные.
· 1 июня три пары дадут приплод, и мы получим 8 пар кроликов (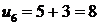 ), 3 из которых новорожденные.
), 3 из которых новорожденные.
· 1 июля мы получим 13 пар – 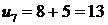 .
.
И так далее… В итоге 1 января следующего года получим 233 пары. Из построения следует, что 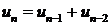 , в то время как
, в то время как 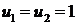 .
.
Таким образом, получили рекуррентное соотношение 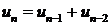 с начальными условиями
с начальными условиями 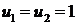 , что позволяет последовательно вычислять элементы последовательности, которые называются числами Фибоначчи.
, что позволяет последовательно вычислять элементы последовательности, которые называются числами Фибоначчи.
Можно показать, что существует бесконечно много последовательностей, удовлетворяющих данному рекуррентному соотношению, каждая из которых однозначно определяется начальными условиями.
Решение рекуррентных соотношений
Определение. Рекуррентное соотношение для последовательности 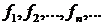 имеет порядок
имеет порядок 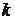 , если оно позволяет выразить элемент
, если оно позволяет выразить элемент 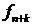 через
через 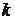 предыдущих элементов:
предыдущих элементов:  .
.
Например, рекуррентное соотношение 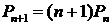 является рекуррентным соотношением порядка 1, а рекуррентное соотношение
является рекуррентным соотношением порядка 1, а рекуррентное соотношение 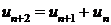 имеет порядок 2, а соотношение
имеет порядок 2, а соотношение 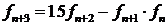 – порядок 3.
– порядок 3.
Зная рекуррентное соотношение порядка 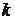 и значения
и значения 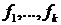 , мы можем один за другим выписывать члены последовательности, но не можем вычислить следующий член, не зная предыдущий. Это не всегда удобно, и часто возникает необходимость найти формулу, выражающую
, мы можем один за другим выписывать члены последовательности, но не можем вычислить следующий член, не зная предыдущий. Это не всегда удобно, и часто возникает необходимость найти формулу, выражающую 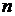 -ый элемент
-ый элемент 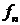 последовательности только как функцию от его номера
последовательности только как функцию от его номера 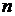 .
.
Определение. Формула, выражающая 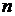 -ый элемент последовательности
-ый элемент последовательности 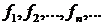 , заданной некоторым рекуррентным соотношением порядка
, заданной некоторым рекуррентным соотношением порядка 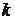 , как функцию от
, как функцию от 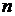 , называется решением данного рекуррентного соотношения.
, называется решением данного рекуррентного соотношения.
При этом последовательность 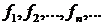 , удовлетворяющая заданному рекуррентному соотношению и выражаемая полученной функцией от
, удовлетворяющая заданному рекуррентному соотношению и выражаемая полученной функцией от 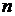 , также называется решением данного рекуррентного соотношения.
, также называется решением данного рекуррентного соотношения.
Например, формула  , дающая последовательность 1, 2, 6, 24, 120, 720,…, является одним из решений рекуррентного соотношения
, дающая последовательность 1, 2, 6, 24, 120, 720,…, является одним из решений рекуррентного соотношения 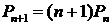 .
.
Определение. Решение рекуррентного соотношения 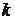 -го порядка называется общим, если оно зависит от
-го порядка называется общим, если оно зависит от 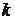 констант
констант 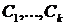 , и путем подбора этих констант можно получить любое решение данного рекуррентного соотношения.
, и путем подбора этих констант можно получить любое решение данного рекуррентного соотношения.
Так, общим решением для рекуррентного соотношения 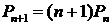 будет формула
будет формула 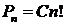 , где
, где 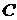 – произвольная постоянная. Действительно, с одной стороны, имеет место равенство
– произвольная постоянная. Действительно, с одной стороны, имеет место равенство 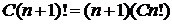 , т.е. формула
, т.е. формула 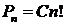 дает одно из решений рекуррентного соотношения
дает одно из решений рекуррентного соотношения 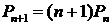 . С другой стороны, любое решение соотношения однозначно определяется величиной
. С другой стороны, любое решение соотношения однозначно определяется величиной 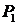 . То есть, если
. То есть, если 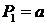 , то
, то 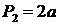 ,
, 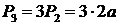 , …,
, …, 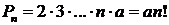 . Т.е. мы получили решение рекуррентного соотношения, которое получается при выборе константы
. Т.е. мы получили решение рекуррентного соотношения, которое получается при выборе константы 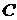 .
.
Для решения рекуррентных соотношений общих правил, вообще говоря, нет. Однако существует весьма часто встречаемый класс соотношений, решаемых общим методом. Это линейные рекуррентные соотношения с постоянными коэффициентами.
Определение. Линейным рекуррентным соотношением порядка 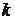 с постоянными коэффициентами называется соотношение вида
с постоянными коэффициентами называется соотношение вида
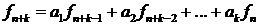 ,
,
где 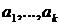 – произвольные постоянные.
– произвольные постоянные.
Рассмотрим эти соотношения при 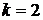 и найдем общее решение линейного рекуррентного соотношения
и найдем общее решение линейного рекуррентного соотношения 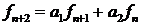 второго порядка с постоянными коэффициентами.
второго порядка с постоянными коэффициентами.
Решение основано на исследовании решений квадратного уравнения 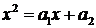 , называемого характеристическим уравнением рекуррентного соотношения
, называемого характеристическим уравнением рекуррентного соотношения 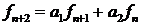 .
.
Теорема. Если уравнение 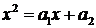 имеет два различных корня
имеет два различных корня 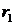 и
и 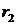 , то общее решение рекуррентного соотношения
, то общее решение рекуррентного соотношения 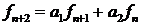 имеет вид
имеет вид 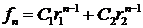 , где
, где 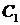 и
и 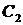 – произвольные постоянные. Если уравнение имеет два совпавших корня
– произвольные постоянные. Если уравнение имеет два совпавших корня 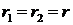 , то общее решение рекуррентного соотношения примет вид
, то общее решение рекуррентного соотношения примет вид 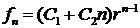 , где
, где 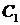 и
и 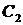 – произвольные постоянные.
– произвольные постоянные.
Линейное рекуррентное соотношение 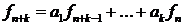 порядка
порядка 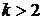 решается тем же способом. Составляем характеристическое уравнение
решается тем же способом. Составляем характеристическое уравнение 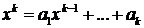 . Если все
. Если все 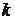 корней различны, то общее решение имеет вид
корней различны, то общее решение имеет вид
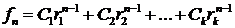 .
.
В том случае, когда имеется корень 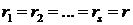 кратности
кратности 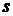 , то этому корню соответствуют решения, дающие в общем решении вклад
, то этому корню соответствуют решения, дающие в общем решении вклад
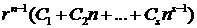 .
.
Пример. Рассмотрим линейное рекуррентное соотношение
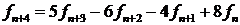
Четвертого порядка с постоянными коэффициентами. Характеристическое уравнение данного соотношения имеет вид
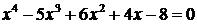 .
.
Найдем корни этого уравнения: 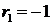 ,
, 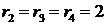 . Следовательно, общее решение соотношения имеет вид
. Следовательно, общее решение соотношения имеет вид
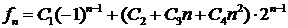 .
.
Пример. Рекуррентное соотношение для чисел Фибоначчи имеет вид 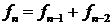 , то есть, является линейным рекуррентным соотношением с постоянными коэффициентами (
, то есть, является линейным рекуррентным соотношением с постоянными коэффициентами (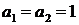 ) второго порядка. Характеристическое уравнение данного соотношения имеет вид
) второго порядка. Характеристическое уравнение данного соотношения имеет вид 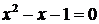 . Оно имеет два различных корня:
. Оно имеет два различных корня:
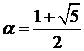 и
и 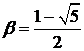 ,
,
следовательно, общее решение соотношения имеет вид
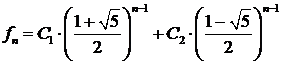 .
.
Найдем 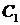 и
и 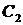 , зная, что
, зная, что 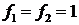 . Для этого рассмотрим систему
. Для этого рассмотрим систему
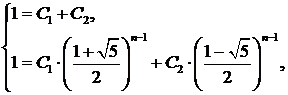
из которой следует, что
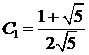 ,
, 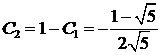 .
.
Тогда частное решение, соответствующее указанным начальным условиям, принимает вид
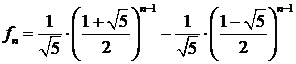 .
.
Таким образом, мы получили формулу, которая позволяет вычислить 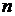 -е число Фибоначчи как функцию его номера без использования информации о предыдущих элементах последовательности.
-е число Фибоначчи как функцию его номера без использования информации о предыдущих элементах последовательности.
Задачи
Найти общее решение линейного рекуррентного соотношения.
1. 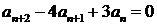 ;
;
2. 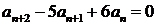 ;
;
3. 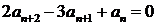 ;
;
4. 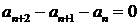 ;
;
5. 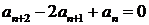 ;
;
6. 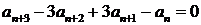 ;
;
7. 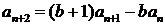 ;
;
8. 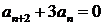 ;
;
9. 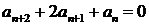 ;
;
10. 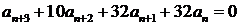 ;
;
11. 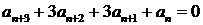 ;
;
12. 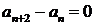 .
.
Найти частное решение линейного рекуррентного соотношения.
1. 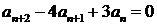 ;
; 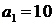 ,
, 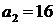 .
.
2. 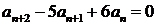 ;
; 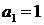 ,
, 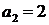 .
.
3. 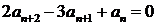 ;
; 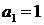 ,
, 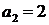 .
.
4. 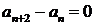 ;
; 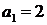 ,
, 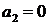 .
.
5. 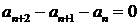 ;
; 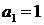 ,
, 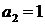 .
.
6. 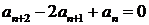 ;
; 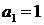 ,
, 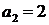 .
.
7. 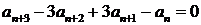 ;
; 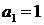 ,
, 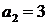 ,
, 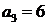 .
.
8. 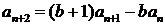 ;
; 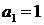 ,
, 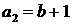 .
.
9. 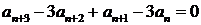 ;
; 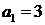 ,
, 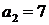 ,
, 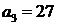 .
.
10. 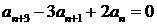 ;
; 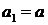 ,
, 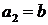 ,
, 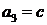 .
.
11. 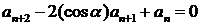 ;
; 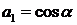 ,
, 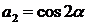 .
.
12. 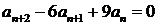 ;
; 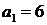 ,
, 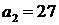 .
.