По изображению предмета на одной плоскости проекций во многих случаях нельзя судить о его форме и размерах. Предметы, показанные на рис. 1, – прямоугольная пластинка, треугольная призма, прямоугольный параллелепипед и параллелепипед с частью цилиндра, – дают в этом случае одинаковые проекции в виде прямоугольника.
По одной проекции можно судить лишь о двух измерениях предмета.
Но и две проекции предмета часто недостаточно полно отображают его форму. Так, например, две проекции прямоугольного параллелепипеда (рис. 1, а, б) неоднозначно отображают его форму. Такие две проекции могут иметь и треугольная призма (рис. 1, в), и призма с закруглением (рис. 1, г), и т.д.
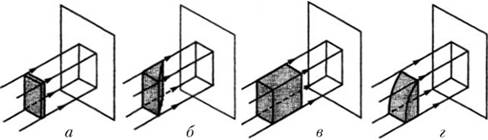
Рисунок 1 - Проекции разных по форме предметов на одну плоскость
Чтобы получить полное представление о форме и размерах предмета, его нужно спроецировать на две, три или более плоскостей. Для простоты проецирования эти плоскости располагают взаимно перпендикулярно. Таким образом, три плоскости образуют прямой трехгранный угол (рис. 2, а). Каждой плоскости даны название и обозначение (рис. 2 а, б).
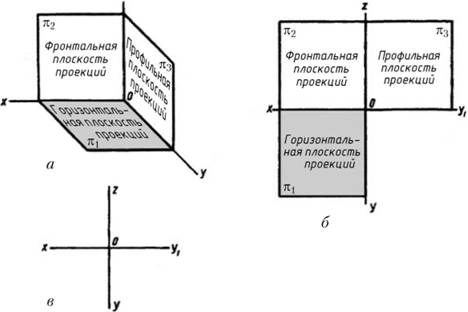
Рисунок 2 - Плоскости проекций
Вертикальная плоскость, расположенная прямо перед нами, называется фронтальной плоскостью проекций. Она обозначается латинской буквой π 2. Под прямым углом к ней горизонтально располагается плоскость проекций, называемая горизонтальной плоскостью. Она обозначается латинской буквой π1. Перпендикулярно этим плоскостям располагается еще одна вертикальная плоскость, обозначенная буквой π3, называемая профильной плоскостью проекций. Попарное пересечение плоскостей трехгранного угла образует прямые линии – оси проекций, исходящие из точки О. Пересечение фронтальной и горизонтальной плоскостей проекций образует ось х, фронтальной и профильной – ось z1, профильной и горизонтальной – ось у (рис. 2, б).
На рис. 2, а изображен трехгранный угол. Его грани взаимно перпендикулярны и не лежат в одной плоскости. Однако чертеж выполняется на плоскости. Для того чтобы изображения, полученные на сторонах трехгранного угла, оказались в одной плоскости, две грани этого угла развертывают до совмещения с третьей гранью, т.е. до такого положения, когда все три плоскости трехгранного угла окажутся в одной плоскости. Для этого горизонтальную плоскость поворачивают вокруг оси х вниз на 90°, профильную плоскость – вокруг оси z на 90° вправо, как показано стрелками. Тогда обе эти плоскости совмещаются с неподвижной фронтальной. При этом горизонтальная плоскость располагается под фронтальной, а профильная – справа от нее (рис. 2, б).
Ось у как бы распадается на две: у и у 1.
Линии, ограничивающие плоскости проекций квадратами, взяты условно и значения не имеют, поэтому их обычно не проводят. Тогда плоскости проекций изобразятся, как показано на рис. 2, в.
Для того чтобы получить ортогональные проекции точки А, необходимо из этой точки опустить перпендикуляры на плоскости проекций.
Точки пересечения этих перпендикуляров с плоскостями проекций образуют проекции точки А:
А1 – горизонтальную проекцию точки;
А2 – фронтальную проекцию точки;
А3 – профильную проекцию точки.
 .
.
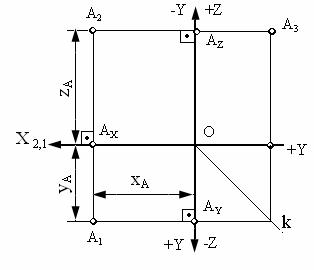
Рисунок 3 - Эпюр точки А
На рис. 3 плоскости проекций π1 и π3 совмещены с плоскостью чертежа (с плоскостью проекции π2), а вместе с ними совмещены с плоскостью чертежа и проекции точки А (А1, А2, А3) и таким образом получена плоскостная модель координатных плоскостей проекций и плоскостная модель пространственной точки А – ее эпюра.
Положение проекций точки А на эпюре однозначно определяется ее тремя координатами (рис. 3).
Домашнее задание.
1. Кратко законспектировать материал на тему: «Плоскости и оси проекций, их обозначение. Координаты точек».
2. Выучить материал из учебника Хаскин,А.М. Черчение: учебник для техникумов/ А.М. Хаскин; Под ред. А.В. Блиока. - 3-е изд., перераб. и доп. - К.: Вища школа, 1979. - с.72-76.
3. Ответить на следующие вопросы:
3.1. Как называют и обозначают три основные плоскости проекций?
3.2. Как обозначают оси проекций?
3.3. Что такое комплексный чертёж точки и как его получают?
3.4. Каковы основные положения проецирования точки?