ЦИФРОВАЯ ЭЛЕКТРОНИКА.
7.1 Позиционная система счисления
Пример непозиционной системы счисления – Римская система, в которой значение цифры не зависит от местоположение: ХХVI – X везде равно 10. В позиционной системе значимость цифры определяется ее местоположением. Представляется в виде полинома число х
 ,
,
где хi – разрядный коэффициент (хi = 0…q-1); qi – весовой коэффициент; q – основание системы счисления (может быть целым и дробным). Наиболее распространена в цифровой технике двоичная система счисления(q = 2) (табл. 7.1).
 Существуют также позиционные системы с q =2,8,10 и 16. Переход от системы счисления с меньшим основанием к системе с большим основанием осуществляется по вышеприведенному выражению.
Существуют также позиционные системы с q =2,8,10 и 16. Переход от системы счисления с меньшим основанием к системе с большим основанием осуществляется по вышеприведенному выражению.
Пример: Преобразовать двоичное число х2 = 10112 в десятичное х10.
Для q =2 х10=1×23+ 1×22 +0×21 +1×20 =11
Переход от системы счисления с большим основанием к системе счисления с меньшим основанием: а) целая часть исходного числа делится на основание новой системы счисления; б)дробная часть исходного числа умножается на основание новой системы счисления.
Булева алгебра. Буль – ирландский математик, середина 19 в. Служит для описания алгоритмов цифровых устройств. Оперируют логической 1 (около 5 В) и логическим 0 (около 0,2 В).
7.2Основные способы записи функций алгебры логики (ФАЛ)

 |
Функции алгебры логики (ФАЛ) – зависимость выходных переменных Zi, выраженная через совокупность входных переменных х1,х2,…хn. Логические устройства – работа которых описывается с помощью ФАЛ.
1) Описание ФАЛ в виде таблице истинности (табл. 7.2).
2) Описание ФАЛ в виде алгебраического выражения:
а) логическое сложение (ИЛИ) – дизъюнкция

 |
 б) логическое умножение (И) – конъюнкция
б) логическое умножение (И) – конъюнкция
в) отрицание, инверсия (НЕ) если х = 1, то  ;если х = 0, то
;если х = 0, то 

Дизъюнктивная нормальная форма (ДНФ) – логическая сумма логических произведений, в каждое из которых аргумент входит один раз. ДНФ может быть получена из таблицы истинности по следующим правилам: 1) Записывают произведение входных переменных, для которых ФАЛ равна единице, причем переменные, равные нулю, записывают с инверсией. Эти произведения называют конституентами единицы; 2) Логически суммируют все конституенты единицы ДНФ. Полученная суммированием конституент единиц сумма, называется СДНФ – совершенная ДНФ.
Конъюнктивная нормальная форма (КНФ) – логическое произведение логических сумм, в каждую из которых аргумент или его инверсия входят один раз. КНФ может быть получена из таблицы истинности по следующим правилам: 1) Записывают суммы входных переменных, для которых ФАЛ равна нулю. При этом переменные, значения которых равны единице, записывают с инверсией. Полученные суммы называют конституентами нуля.
Примеры:
с ДНФ: 
с КНФ: 
1)  Кубическое представление ФАЛ. При этом набор выходных переменных представляется n – мерным вектором. Вершины этих векторов геометрически могут быть представлены как вершины n – мерного куба (рис. 7.1). Отмечая точками вершины этих векторов, для которых ФАЛ равна единице, получаем геометрическое представление в виде куба.
Кубическое представление ФАЛ. При этом набор выходных переменных представляется n – мерным вектором. Вершины этих векторов геометрически могут быть представлены как вершины n – мерного куба (рис. 7.1). Отмечая точками вершины этих векторов, для которых ФАЛ равна единице, получаем геометрическое представление в виде куба.
Например, задана ФАЛ z(х2, x1, x0) = å(3,4,5,6,7); Дать геометрическое представление в виде куба. Графическое решение задачи представлено на рисунке.
2) Соседние наборы переменных, расположенные на концах ребер куба, отличаются только одной переменной. Каждую вершину куба, в которой функция принимает единичное значение, называют нулевым кубом. Множество нулевых кубов составляет кубический комплекс К0 ФАЛ. Если два нулевых куба комплекса К0 отличаются по одной переменной, для которых ФАЛ равна единице, являются соседними, то они образуют единичный куб. Геометрически это соответствует ребру исходного n – мерного куба (рисунок 7.2 а).
 |
1 – куб записывается последовательностью общих элементов образовавших его 0 – кубов с прочерком совпадающих элементов. Множество единичных кубов образует единичный кубический комплекс К1.
Если два единичных куба комплекса К1 отличаются только по одной координате (переменной), то эти единичные кубы образуют двоичный куб. Геометрически это соответствует грани исходного n – мерного куба (рис. 7.2). 2 – куб записывается последовательностью общих элементов, образовавших его 1 – кубов с прочерком несовпадающих элементов.
Пример: Задана ФАЛ z(х2, x1, x0) = å(3,4,5,6,7). Записать кубические комплексы.
Решение: Нулевой кубический комплекс К0=(011,100,101,110,111). 1-ый и 5-ый кубы отличаются только первым членом. Поэтому они образуют 1-куб вида – 11. Аналогично второй и третий 0-кубы образуют 1- куб 10 – и т.д. Единичный кубический комплекс заданной ФАЛ будет иметь вид: К=(-11,10-,1-0,11-,1-1). Аналогично получается двоичный кубический комплекс, состоящий из одного 2-куба: К2=(1--).
7.3 Теоремы Булевой алгебры
1 х+0=х; х+1=1;х+х=х; 
2 х×1=х; х×0=0; х×х=х; 
3  ;
;
4 х1+х0=х0+х1; х1×х0=х0×х1 Переместительный закон;
5 (х2+х1)+х0=х2+(х1+х0); (х1×х2)×х0= х1×(х2×х0) Сочетательный закон
6 Теорема Де – Моргана  ;
;  ;
; 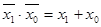 ;
; 
7 Теорема поглощения х1×х0+х0= х0; (х1+ х0)× х0= х0
8 х2×х1+ х0=(х1+ х0)(х2+ х0); (х2+х1) х0= х0; (х1+х0) х0= х0;
9  ;
;  ;
;
10  ;
; 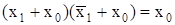 - теорема склеивания.
- теорема склеивания.