Призма и сфера.
Определение 2.3.1.
Призма называется вписанной в сферу, если все ее вершины лежат на поверхности сферы.
Определение 2.3.2.
Если призма вписана в сферу, то сфера называется описанной около призмы.
Центр О* описанной около призмы сферы - это точка, равноудаленная от всех вершин призмы.

|
Рассмотрим правильную треугольную призму АВСА1В1С1. Если О – центр окружности, описанной около треугольника АВС, а О1- около треугольника А1В1С1, то прямая ОО1 (она перпендикулярна плоскостям основания) является геометрическим местом точек, равноудаленных от вершин А, В, С; она же является геометрическим местом точек, равноудаленных от вершин А1,В1,С1. Осталось найти на этой прямой точку, равноудаленную от всех вершин призмы. Очевидно, что это середина отрезка ОО1- точка О*: АО*=ВО*=СО*=А1О*=В1О*=С1О*. Таким образом, точка О*- центр описанной около призмы АВСА1В1С1 сферы.
Около любой правильной призмы всегда можно описать сферу.
Следует отметить, что описать сферу можно также около прямой призмы, в основании которой лежит произвольный многоугольник, если около него можно описать окружность.
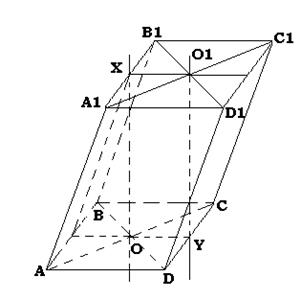
Наклонную призму в сферу нельзя вписать, так как не существует точки, равноудаленной от всех ее вершин. Рассмотрим наклонную призму, в основании которой квадрат.
|
Геометрическое место точек в пространстве, равноудаленных от вершин А,В,С и D - перпендикуляр ОХ к плоскости основания, от вершин А1, В1, С1, D1- перпендикуляр О1Y (О, О1 центры окружностей, описанных около квадратов АВСD и А1В1С1D1 соответственно). Так как основания призмы параллельны, то параллельны и перпендикуляры к ним, то есть ОХ׀׀О1Y, а следовательно не существует точки, равноудаленной от всех вершин наклонной призмы (чтобы она существовала, прямые ОХ и О1Y должны пересекаться).
Пирамида и сфера.
Определение 2.4.1. Пирамида (усеченная пирамида) называется вписанной в сферу, если все ее вершины лежат на поверхности сферы.
Определение 2.4.2.
Если пирамида (усеченная пирамида) вписана в сферу, то сфера называется описанной около пирамида (усеченная пирамида).
Центр О’ описанной около пирамиды сферы – точка, равноудаленная от вершин пирамиды.
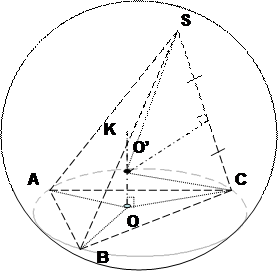
Рассмотрим правильную треугольную пирамиду SАВС.
|
Геометрическое место точек в пространстве равноудаленных от трех данных, есть прямая, являющаяся линией пересечения плоскостей, проходящих через середины отрезков, образованных данными точками, перпендикулярно им. Другими словами, это перпендикуляр, восстановленный к плоскости треугольника, образованного данными точками, в центре описанной около него окружности. В данном случае прямая ОК – это геометрическое место точек, равноудаленных от вершин А, В и С. Чтобы найти на этой прямой точку, равноудаленную от вершин S и С (а значит, и от А и В), проведем через середину SС перпендикулярную ему плоскость, которая пересечет прямую ОК в некоторой точке О’. Эта точка, равноудаленная от всех вершин пирамиды и является центром описанной около этой пирамиды сферы. Следовательно, описать сферу можно около любой пирамиды в основании которой правильный многоугольник. Это возможно и в том случае, когда в основании пирамиды лежит произвольный многоугольник, если он вписывается в окружность.
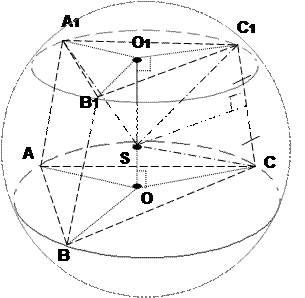
Рассмотрим усеченную пирамиду АВСА1В1С1, высота ОО1 которой соединяет центры верхнего и нижнего оснований, являющихся правильными треугольниками.
|
Центр описанной сферы - это точка равноудаленная от всех вершин многогранника. Эта точка находится на прямой ОО1, являющейся геометрическим местом точек, равноудаленных от вершин А, В, С и от вершин А1, В1, С1 (О и О1 – центры описанных окружностей около треугольников АВС и А1В1С1 соответственно). Проведем через середину бокового ребра, например, АА1 перпендикулярную ему плоскость, которая пересечет прямую ОО1 в некоторой точке S. Из треугольника АА1S видно, что точка S равноудалена от вершин А (а значит, и от В1 и С1). Таким образом, мы определим центр описанной сферы: это точка S.
Если бы усеченная пирамида была образована от пирамиды, у которой вершина проектируется не в центр основания, то такой точки S бы не существовало, то есть описать сферу было бы невозможно (ведь геометрические места точек в пространстве, равноудаленных от вершин нижнего основания и от вершин верхнего основания усеченной пирамиды, не пересекались бы).
Если в основании прямой усеченной пирамиды будут лежать произвольные выпуклые многоугольники, которые можно будет вписывать в окружность, то такую усеченную пирамиду можно будет вписать в сферу.