Угол между двумя прямыми l1:y=k1x+b1 и l2:k2y=b2 определяется по формуле:
Tga=+-(k2-k1)/1+k1*k2>=0
Условия параллельности двух прямых:
а) Если прямые заданы уравнениями с угловым коэффициентом, то необходимое и достаточное условие их параллельности состоит в равенстве их угловых коэффициентов:
k 1 = k 2.
б) Для случая, когда прямые заданы уравнениями в общем виде A 1 x + B 1 y + C 1 = 0,
A 2 x + B 2 y + C 2 = 0,
необходимое и достаточное условие их параллельности состоит в том, что коэффициенты при соответствующих текущих координатах в их уравнениях пропорциональны, т. е.
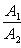
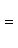
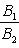

Условия перпендикулярности двух прямых:
а) В случае, когда прямые заданы уравнениями с угловым коэффициентом, необходимое и достаточное условие их перпендикулярности заключается в том, что их угловые коэффициенты обратны по величине и противоположны по знаку, т. е.
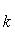
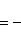
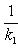

24)Взаимное расположение прямой и плоскости в пространстве.Точка пересечения прямой и плоскости.
1) Взаимное расположение прямой и плоскости в пространстве.
Прямая может лежать на данной плоскости, быть параллельна данной плоскости или пересекать ее в одной точке, см. следующие рисунки.
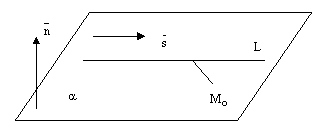
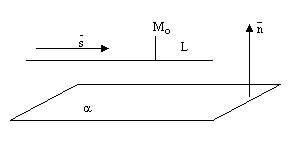
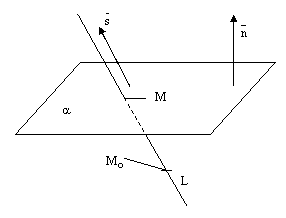
рис.8.
Теорема. Пусть плоскость 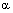 задана общим уравнением
задана общим уравнением 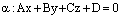 ,
,
а прямая L задана каноническими уравнениями 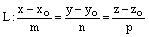
или параметрическими уравнениями
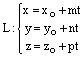 ,
, 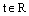 ,
,
в которых 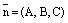 – координаты нормального вектора плоскости
– координаты нормального вектора плоскости 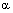 ,
, 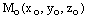 – координаты произвольной фиксированной точки прямой L,
– координаты произвольной фиксированной точки прямой L, 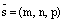 –
–
координаты направляющего вектора прямой L. Тогда:
1) если 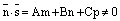 , то прямая L пересекает плоскость
, то прямая L пересекает плоскость 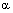 в точке, координаты которой
в точке, координаты которой 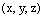 можно найти из системы уравнений
можно найти из системы уравнений
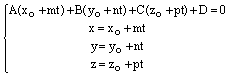 ; (7)
; (7)
2) если 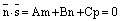 и
и 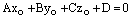 , то прямая лежит на плоскости;
, то прямая лежит на плоскости;
3) если 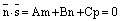 и
и 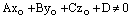 , то прямая параллельна плоскости.
, то прямая параллельна плоскости.
Доказательство. Условие 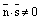 говорит о том, что вектроры
говорит о том, что вектроры 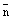 и
и 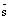 не ортогональны, а значит прямая не параллельна плоскости и не лежит в плоскости, а значит пересекает ее в некоторой точке М. Координатыточки М удовлетворяют как уравнению плоскости, так и уравнениям прямой, т.е. системе (7). Решаем первое уравнение системы (7) относительно неизвестной t и затем, подставляя найденное значение t в остальные уравнения системы, находим координаты искомой точки.
не ортогональны, а значит прямая не параллельна плоскости и не лежит в плоскости, а значит пересекает ее в некоторой точке М. Координатыточки М удовлетворяют как уравнению плоскости, так и уравнениям прямой, т.е. системе (7). Решаем первое уравнение системы (7) относительно неизвестной t и затем, подставляя найденное значение t в остальные уравнения системы, находим координаты искомой точки.
Если 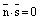 , то это означает, что
, то это означает, что 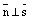 . А такое возможно лишь тогда, когда прямая лежит на плоскости или параллельна ей. Если прямая лежит на плоскости, то любая точка прямой является точкой плоскости и координаты любой точки прямой удовлетворяют уравнению плоскости. Поэтому достаточно проверить, лежит ли на плоскости точка
. А такое возможно лишь тогда, когда прямая лежит на плоскости или параллельна ей. Если прямая лежит на плоскости, то любая точка прямой является точкой плоскости и координаты любой точки прямой удовлетворяют уравнению плоскости. Поэтому достаточно проверить, лежит ли на плоскости точка 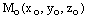 . Если
. Если 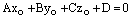 , то точка
, то точка 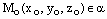 – лежит на плоскости, а это означает, что и сама прямая лежит на плоскости.
– лежит на плоскости, а это означает, что и сама прямая лежит на плоскости.
Если 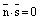 , а
, а 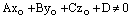 , то точка на прямой не лежит на плоскости, а это означает, что прямая параллельна плоскости.
, то точка на прямой не лежит на плоскости, а это означает, что прямая параллельна плоскости.
Теорема доказана.
2)Найти точку пересечения прямой 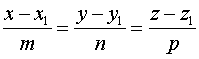 и плоскости
и плоскости  .
.
1. Находим параметрические уравнения прямой. Для этого полагаем
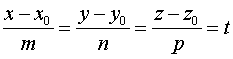 ,
,
откуда получаем
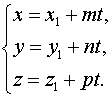
2. Подставляя эти выражения для  в уравнение плоскости и решая его относительно
в уравнение плоскости и решая его относительно 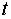 , находим значение параметра
, находим значение параметра 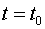 , при котором происходит пересечение прямой и плоскости.
, при котором происходит пересечение прямой и плоскости.
3. Найденное значение 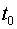 подставляем в параметрические уравнения прямой и получаем искомые координаты точки пересечения:
подставляем в параметрические уравнения прямой и получаем искомые координаты точки пересечения:
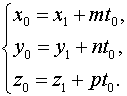
Замечание. Если в результате решения уравнения относительно параметра 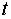 получим противоречие, то прямая и плоскость параллельны (это эквивалентно условию
получим противоречие, то прямая и плоскость параллельны (это эквивалентно условию 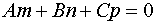 ).
).
25)Канонические уравнения окружности,эллипса,гиперболы и параболы.
30)Основные элементарные функции и их графики.
| 1. |  Пропорциональные величины. Если переменные y и x прямо пропорциональны, то функциональная зависимость между ними выражается уравнением:
y = k x, где k - постоянная величина (коэффициент пропорциональности).
График прямой пропорциональности – прямая линия, проходящая через начало координат и образующая с осью X угол Пропорциональные величины. Если переменные y и x прямо пропорциональны, то функциональная зависимость между ними выражается уравнением:
y = k x, где k - постоянная величина (коэффициент пропорциональности).
График прямой пропорциональности – прямая линия, проходящая через начало координат и образующая с осью X угол 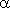 , тангенс которого равен k: tan , тангенс которого равен k: tan 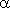 = k (рис.8). Поэтому, коэффициент пропорциональности называетсятакже угловым коэффициентом. На рис.8 показаны три графика для k = 1/3, k = 1 и k = 3. = k (рис.8). Поэтому, коэффициент пропорциональности называетсятакже угловым коэффициентом. На рис.8 показаны три графика для k = 1/3, k = 1 и k = 3.
|
| 2. |  Линейная функция. Если переменные y и x связаны уравнением 1-ой степени:
A x + B y = C,где по крайней мере одно из чисел A или B не равно нулю, то графиком этой функциональной зависимости является прямая линия. Если C = 0, то она проходит через начало координат, в противном случае - нет. Графики линейных функций для различных комбинаций A, B, C показаны на рис.9. Линейная функция. Если переменные y и x связаны уравнением 1-ой степени:
A x + B y = C,где по крайней мере одно из чисел A или B не равно нулю, то графиком этой функциональной зависимости является прямая линия. Если C = 0, то она проходит через начало координат, в противном случае - нет. Графики линейных функций для различных комбинаций A, B, C показаны на рис.9.
|
| 3. | 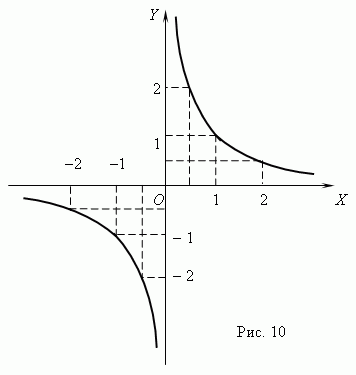 Обратнаяпропорциональность. Если переменные y и x обратно пропорциональны, то функциональная зависимость между ними выражается уравнением:
y = k / x, где k - постоянная величина.
График обратной пропорциональности – гипербола (рис.10). В общем случае эта величина равна k, что следует из уравнения гиперболы: xy = k. Обратнаяпропорциональность. Если переменные y и x обратно пропорциональны, то функциональная зависимость между ними выражается уравнением:
y = k / x, где k - постоянная величина.
График обратной пропорциональности – гипербола (рис.10). В общем случае эта величина равна k, что следует из уравнения гиперболы: xy = k.
|
| 5. | 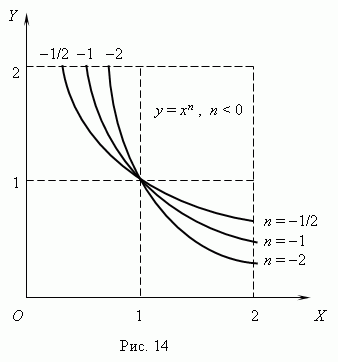 Степенная функция. Это функция: y = axn, где a, n – постоянные. При n = 1 получаем прямую пропорциональность: y = ax; при n = 2 - квадратную параболу; при n = 1 - обратную пропорциональность или гиперболу. Степенная функция. Это функция: y = axn, где a, n – постоянные. При n = 1 получаем прямую пропорциональность: y = ax; при n = 2 - квадратную параболу; при n = 1 - обратную пропорциональность или гиперболу.
 Если n – целые, степенные функции имеют смысл и при x < 0, но их графики имеют различный вид в зависимости от того, является ли n чётным числом или нечётным. На рис.15 показаны две такие степенные функции: для n = 2 и n = 3.
Если n – целые, степенные функции имеют смысл и при x < 0, но их графики имеют различный вид в зависимости от того, является ли n чётным числом или нечётным. На рис.15 показаны две такие степенные функции: для n = 2 и n = 3.
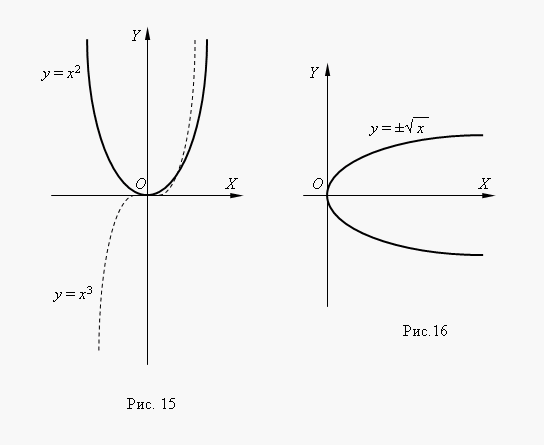 При n = 2 функция чётная и её график симметричен относительно оси Y. При n = 3 функция нечётная и её график симметричен относительно начала координат. Функция y = x 3 называется кубической параболой.
На рис.16 представлена функция
При n = 2 функция чётная и её график симметричен относительно оси Y. При n = 3 функция нечётная и её график симметричен относительно начала координат. Функция y = x 3 называется кубической параболой.
На рис.16 представлена функция 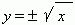 . Эта функция является обратной к квадратной параболе y = x 2 . Эта функция является обратной к квадратной параболе y = x 2
|
| 6. | 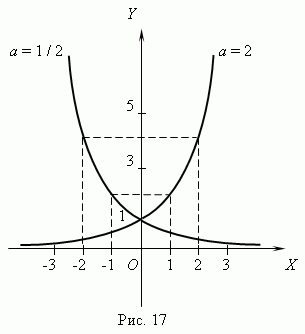 Показательная функция. Функция y = ax, где a - положительное постоянное число, называется показательной функцией. Аргумент x принимает любые действительные значения; в качестве значений функции рассматриваются только положительные числа, так как иначе мы имеем многозначную функцию. Так, функция y = 81 x имеет при x = 1/4 четыре различных значения: y = 3, y = 3, y = 3 i и y = 3 i (проверьте, пожалуйста!).Но мы рассматриваем в качестве значения функции только y = 3. Показательная функция. Функция y = ax, где a - положительное постоянное число, называется показательной функцией. Аргумент x принимает любые действительные значения; в качестве значений функции рассматриваются только положительные числа, так как иначе мы имеем многозначную функцию. Так, функция y = 81 x имеет при x = 1/4 четыре различных значения: y = 3, y = 3, y = 3 i и y = 3 i (проверьте, пожалуйста!).Но мы рассматриваем в качестве значения функции только y = 3.
|
| 7. | 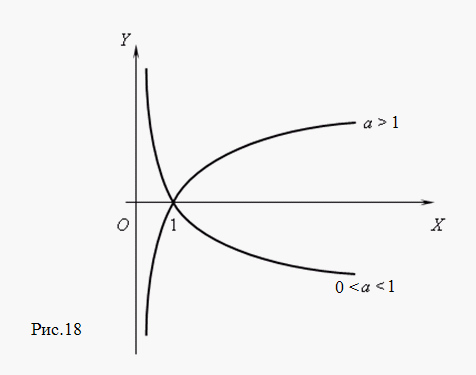 Логарифмическая функция. Функция y = log a x, где a – постоянное положительное число,не равное 1, называется логарифмической. Эта функция является обратной к показательной функции; Логарифмическая функция. Функция y = log a x, где a – постоянное положительное число,не равное 1, называется логарифмической. Эта функция является обратной к показательной функции;
|
| 8. | 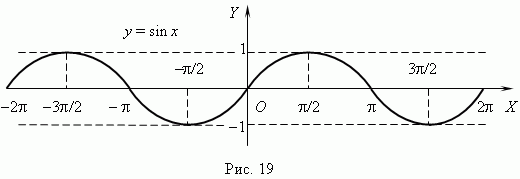 Тригонометрические функции. При построении тригонометрических функций мы используем радианную меру измерения углов.Тогда функция y = sin x представляется графиком (рис.19). Эта кривая называется синусоидой.
График функции y =cos x представлен на рис.20; это такжесинусоида, полученная в результате перемещения графика y =sin x вдоль оси Х влево на Тригонометрические функции. При построении тригонометрических функций мы используем радианную меру измерения углов.Тогда функция y = sin x представляется графиком (рис.19). Эта кривая называется синусоидой.
График функции y =cos x представлен на рис.20; это такжесинусоида, полученная в результате перемещения графика y =sin x вдоль оси Х влево на  2 2
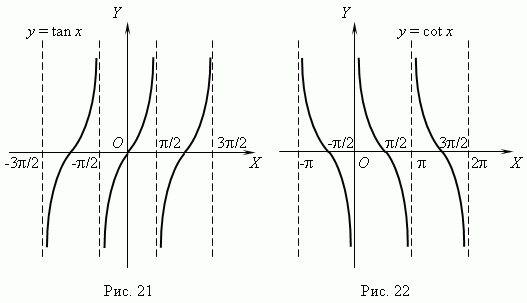 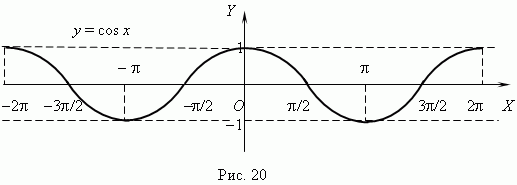 Графики функций y = tan x и y = cot x показаны соответственно на рис.21 и рис.22
Из графиков видно, что эти функции: периодические (их период
Графики функций y = tan x и y = cot x показаны соответственно на рис.21 и рис.22
Из графиков видно, что эти функции: периодические (их период  ), неограниченные, в целом не монотонные, но имеют интервалы монотонности (какие?), разрывные (какие точки разрыва имеют эти функции?). Область определения и область значений этих функций: ), неограниченные, в целом не монотонные, но имеют интервалы монотонности (какие?), разрывные (какие точки разрыва имеют эти функции?). Область определения и область значений этих функций:
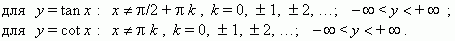
|
| 9. | Обратные тригонометрические функции. |
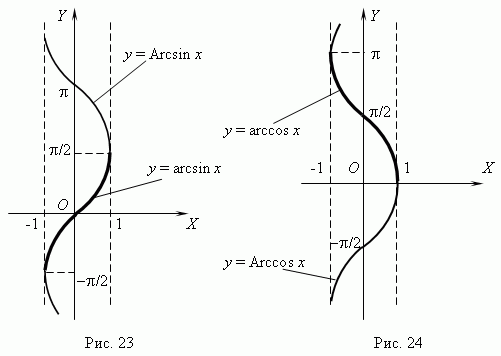 Функции y = Arcsin x (рис.23) и y = Arccos x (рис.24)многозначные, неограниченные; их область определения и область значений соответственно: 1
Функции y = Arcsin x (рис.23) и y = Arccos x (рис.24)многозначные, неограниченные; их область определения и область значений соответственно: 1  x
x  +1 и
+1 и  < y +
< y + 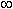 . Поскольку эти функции многозначные,не рассматриваемые в элементарной математике, в качестве обратных тригонометрических функций рассматриваются их главные значения: y = arcsin x и y = arccos x; их графики выделены на рис.23 и рис.24 жирными линиями.
. Поскольку эти функции многозначные,не рассматриваемые в элементарной математике, в качестве обратных тригонометрических функций рассматриваются их главные значения: y = arcsin x и y = arccos x; их графики выделены на рис.23 и рис.24 жирными линиями.
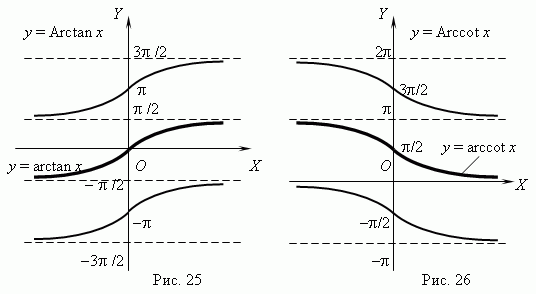
Функции y = Arctan x (рис.25) и y = Arccot x (рис.26)- многозначные, неограниченные; их область определения: 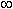
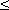 x
x 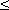 +
+ 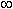 . Их главные значения y = arctan x и y = arccot x рассматриваются в качестве обратных тригонометрических функций; их графики выделены на рис.25 и рис.26 жирными ветвями.
. Их главные значения y = arctan x и y = arccot x рассматриваются в качестве обратных тригонометрических функций; их графики выделены на рис.25 и рис.26 жирными ветвями.
31)Предел переменной величины. Бесконечно большая переменная величина.
Число A называется пределом функции f (x) в точке 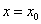 (или при
(или при 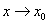 ), если для любой сходящейся к
), если для любой сходящейся к 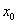 последовательности (1) значений аргумента x, отличных от
последовательности (1) значений аргумента x, отличных от 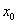 , соответствующая последовательность (2) сходится к числу A.
, соответствующая последовательность (2) сходится к числу A.
Символически это записывается так: 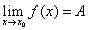
Это означает: чтобы найти предел функции, нужно в функцию вместо x подставить то значение, к которому стремится x.
Переменная величина xn называется бесконечно большой, если, начиная с некоторого номера, она становится и остается при всех последующих номерах по абсолютной величине больше любого наперед заданного положительного числа M. Если xn есть величина бесконечно большая, то это записывается так: lim xn = 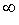 , или xn
, или xn 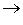
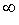 .
.
32)Предел функции в точке и на бесконечности. Односторонние пределы. Необходимые и достаточные условия существования пределов.
Число А называется пределом функции f(x) при 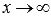 , если для любой бесконечно большой последовательности аргументов функции (бесконечно большой положительной или отрицательной), последовательность значений этой функции сходится к А. Обозначается
, если для любой бесконечно большой последовательности аргументов функции (бесконечно большой положительной или отрицательной), последовательность значений этой функции сходится к А. Обозначается  .
.
Число В называется пределом функции f(x) слева при 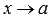 , если для любой сходящейся к а последовательности аргументов функции
, если для любой сходящейся к а последовательности аргументов функции 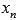 , значения которых остаются меньше а (
, значения которых остаются меньше а (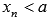 ), последовательность значений этой функции сходится к В.
), последовательность значений этой функции сходится к В.
Обозначается 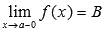 .
.
Число В называется пределом функции f(x) справа при 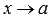 , если для любой сходящейся к а последовательности аргументов функции
, если для любой сходящейся к а последовательности аргументов функции 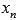 , значения которых остаются больше а (
, значения которых остаются больше а (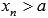 ), последовательность значений этой функции сходится к В.
), последовательность значений этой функции сходится к В.
Обозначается 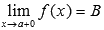 .
.
Предел функции в точке.
Пусть функция f(x) определена на множестве X = {x}, имеющем точку сгущения (предельную точку) a. Запись
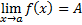 обозначает, что для любого числа ε > 0 cуществует число δ = δ (ε) > 0 такое, что для всех x, для которых f(x) имеет смысл и которые удовлетворяют условию 0 < |x - a| < δ, справедливо неравенство: |f(x)- A |< ε.
обозначает, что для любого числа ε > 0 cуществует число δ = δ (ε) > 0 такое, что для всех x, для которых f(x) имеет смысл и которые удовлетворяют условию 0 < |x - a| < δ, справедливо неравенство: |f(x)- A |< ε.
Имеют место два замечательных предела:
1) 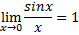
2) 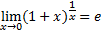
Критерий Коши:
Предел функции f(x) в точке a существует тогда и только тогда, если для каждого ε > 0 найдется такое δ = δ (ε) >0, что
|f(x') - f(x")| < ε, как только 0 < |x' - a| < δ и 0 < |x' - a| < δ, где x' и x" - любые точки из области определения функции f(x).
33)Бесконечно большие функции. Ограниченные функции.

Ограниченность функции.
Функция f(x) называется ограниченной на данном промежутке (a,b), если существуют некоторые числа m и M такие, что
m ≤ f(x) ≤ M
при хє(a,b).
Число mo= inf {f(x)} [x є (a,b)] = max m называется нижней гранью функции,
а число Mo= sup {f(x)} [x є (a,b)]=min M называется верхней гранью функции на данном промежутке (a,b).
Разность Mo- mo называется колебанием функции на промежутке (a,b)
34)Бесконечно малые и их свойства.
Функция y=f(x) называется бесконечно малой при x→a или при x →∞, если 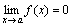 или
или 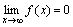 , т.е. бесконечно малая функция – это функция, предел которой в данной точке равен нулю.
, т.е. бесконечно малая функция – это функция, предел которой в данной точке равен нулю.
Теорема. Если функция y=f(x) представима при x→a в виде суммы постоянного числа b и бесконечно малой величины α(x): f (x)=b+ α(x) то 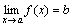 .
.
Обратно, если 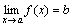 , то f (x)=b+α(x), где a(x) – бесконечно малая при x→a.
, то f (x)=b+α(x), где a(x) – бесконечно малая при x→a.
Доказательство.
Докажем первую часть утверждения. Из равенства f(x)=b+α(x) следует |f(x) – b|=| α|. Но так как a(x) – бесконечно малая, то при произвольном ε найдется δ – окрестность точки a, при всех x из которой, значения a(x) удовлетворяют соотношению |α(x)|< ε. Тогда |f(x) – b|< ε. А это и значит, что 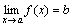 .
.
Если 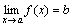 , то при любом ε >0 для всех х из некоторой δ – окрестность точки a будет |f(x) – b|< ε. Но если обозначим f(x) – b= α, то |α(x)|< ε, а это значит, что a – бесконечно малая.
, то при любом ε >0 для всех х из некоторой δ – окрестность точки a будет |f(x) – b|< ε. Но если обозначим f(x) – b= α, то |α(x)|< ε, а это значит, что a – бесконечно малая.
Рассмотрим основные свойства бесконечно малых функций.
Теорема 1. Алгебраическая сумма двух, трех и вообще любого конечного числа бесконечно малых есть функция бесконечно малая.
Доказательство. Приведем доказательство для двух слагаемых. Пусть f(x)=α(x)+β(x), где 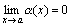 и
и 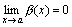 . Нам нужно доказать, что при произвольном как угодно малом ε > 0 найдется δ> 0, такое, что для x, удовлетворяющих неравенству |x – a|<δ, выполняется |f(x)|< ε.
. Нам нужно доказать, что при произвольном как угодно малом ε > 0 найдется δ> 0, такое, что для x, удовлетворяющих неравенству |x – a|<δ, выполняется |f(x)|< ε.
Итак, зафиксируем произвольное число ε > 0. Так как по условию теоремы α(x) – бесконечно малая функция, то найдется такое δ1 > 0, что при |x – a|< δ1 имеем |α(x)|< ε / 2. Аналогично, так как β(x) – бесконечно малая, то найдется такое δ2 > 0, что при |x – a|< δ2 имеем | β(x)|< ε / 2.
Возьмем δ=min{ δ1, δ2 }. Тогда в окрестности точки a радиуса δ будет выполняться каждое из неравенств |α(x)|< ε / 2 и | β(x)|< ε / 2. Следовательно, в этой окрестности будет
|f(x)|=| α(x)+β(x) | ≤ |α(x)| + | β(x)| < ε /2 + ε /2= ε,
т.е. |f(x)|< ε, что и требовалось доказать.
Теорема 2. Произведение бесконечно малой функции a(x) на ограниченную функцию f(x) при x→a (или при x→∞) есть бесконечно малая функция.
Доказательство. Так как функция f(x) ограничена, то существует число М такое, что при всех значениях x из некоторой окрестности точки a|f(x)|≤M. Кроме того, так как a(x) – бесконечно малая функция при x→a, то для произвольного ε > 0 найдется окрестность точки a, в которой будет выполняться неравенство |α(x)|< ε /M. Тогда в меньшей из этих окрестностей имеем | αf|< ε /M = ε. А это и значит, что af – бесконечно малая. Для случая x→∞ доказательство проводится аналогично.
Из доказанной теоремы вытекают:
Следствие 1. Если 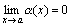 и
и 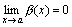 , то
, то 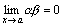 .
.
Следствие 2. Если 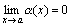 и c= const, то
и c= const, то 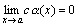 .
.
Теорема 3. Отношение бесконечно малой функции α(x) на функцию f(x), предел которой отличен от нуля, есть бесконечно малая функция.
35)Арифметические свойства пределов.
1° Предел суммы/разности двух функций равен сумме/разности их пределов: 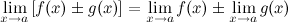
2° Предел произведения двух функций равен произведению их пределов: 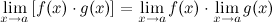
3° Предел частного двух функций равен частному их пределов, при условии, что предел знаменателя не равен нулю: 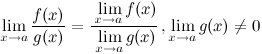
36)Первый замечательный предел.
Первый замечательный предел
Первый замечательный предел:
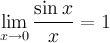
Предел отношения синуса к его аргументу равен единице в случае, когда аргумент стремится к нулю.
Следствия из первого замечательного предела
1° 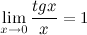
2° 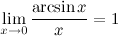
3° 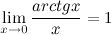
4° 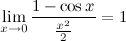
37)Второй замечательный предел.
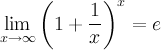
здесь е - число Эйлера.
Следствия из второго замечательного предела
1° 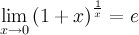
2° 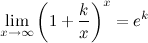
3° 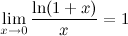
4° 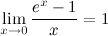
5° 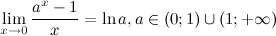
6° 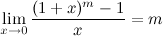
38)Сравнение бесконечно малых.
Определение
Функция 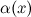 называется бесконечно малой при
называется бесконечно малой при 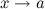 (или в точке
(или в точке 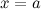 ), если
), если 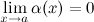
Бесконечно малые функции одного порядка
Пусть 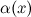 и
и 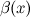 - две б.м. функции при
- две б.м. функции при 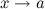 .
.
Определение
Функции 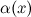 и
и 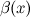 называются б.м. одного порядка малости при
называются б.м. одного порядка малости при 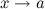 , если
, если 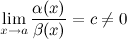
Бесконечно малые функции более низкого и высокого порядков
Определение
Если 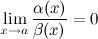 , то
, то 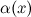 является б.м. более высокого порядка при
является б.м. более высокого порядка при 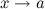 , чем
, чем 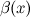 , а
, а 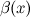 - б.м. более низкого порядка по сравнению с
- б.м. более низкого порядка по сравнению с 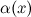 :
: 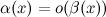 при
при 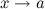 .
.
Определение
Если 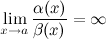 , то
, то 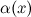 - б.м. низшего порядка малости при
- б.м. низшего порядка малости при 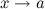 по сравнению с
по сравнению с 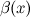 .
.
Определение
Если 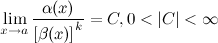 , то
, то 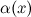 называется б.м. порядка
называется б.м. порядка 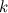 по сравнению с
по сравнению с 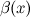 при
при 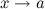 .
.
Пример
Функция 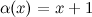 называется б.м. порядка 2 по сравнению с функцией
называется б.м. порядка 2 по сравнению с функцией 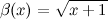 в точке
в точке 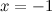 , так как
, так как
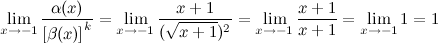
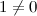 , что и требовалось доказать.
, что и требовалось доказать.
Эквивалентные (равносильные) бесконечно малые функции
Определение
Если 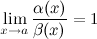 , то б.м. функции
, то б.м. функции 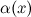 и
и 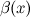 называются эквивалентными или равносильными б.м. одного порядка при
называются эквивалентными или равносильными б.м. одного порядка при 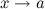 :
: 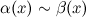 при
при 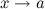 .
.
39)Непрерывность функции в точке. Точка разрыва и их классификация.
Функция 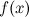 называется непрерывной в точке
называется непрерывной в точке  , если:
, если:
функция 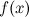 определена в точке
определена в точке  и ее окрестности;
и ее окрестности;
существует конечный предел функции 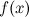 в точке
в точке  ;
;
это предел равен значению функции в точке  , т.е.
, т.е. 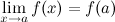
Приращение аргумента и функции
Рассмотрим функцию 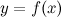 , которая определена в некотором интервале
, которая определена в некотором интервале 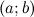 и рассмотрим произвольную точку
и рассмотрим произвольную точку 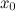 из этого интервала:
из этого интервала: 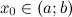 .
.
Приращением аргумента 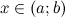 в точке
в точке 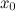 называется разность
называется разность 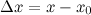
Приращением функции 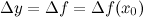 в точке
в точке 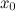 называется разность соответствующих значений функции
называется разность соответствующих значений функции 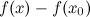 или, используя равенство из выше приведенного замечания, будем иметь:
или, используя равенство из выше приведенного замечания, будем иметь: 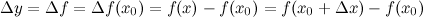
Теорема
Функция 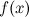 непрерывна в точке
непрерывна в точке  тогда и только тогда, когда бесконечно малому приращению аргумента
тогда и только тогда, когда бесконечно малому приращению аргумента 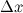 соответствует бесконечно малое приращение функции
соответствует бесконечно малое приращение функции 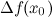 :
:
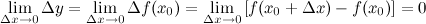
Полезные теоремы о непрерывности функции
Теорема
Если функции 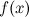 и
и 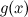 непрерывны в точке
непрерывны в точке  , то функции
, то функции 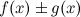 ,
, 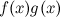 ,
, 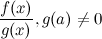 также непрерывны в точке
также непрерывны в точке  .
.
Пусть функция 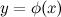 задана на множестве
задана на множестве 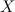 , а
, а 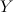 - множество значений этой функции. Пусть на множестве
- множество значений этой функции. Пусть на множестве 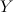 задана функция
задана функция 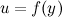 . Тогда говорят, что на множестве
. Тогда говорят, что на множестве 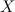 задана композиция функций (или сложная функция)
задана композиция функций (или сложная функция) 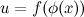 .
.
Теорема
Пусть функция 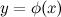 непрерывна в точке
непрерывна в точке  , а функция
, а функция 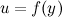 непрерывна в точке
непрерывна в точке 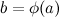 . Тогда композиция функций
. Тогда композиция функций 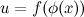 непрерывна в точке
непрерывна в точке  .
.
40)Асимптоты.
Виды асимптот
Определение
Прямая 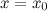 называется вертикальной асимптотой графика функции
называется вертикальной асимптотой графика функции 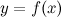 , если хотя бы одно из предельных значений
, если хотя бы одно из предельных значений 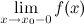 или
или 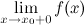 равно
равно 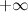 или
или 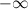 .
.
Замечание. Прямая 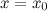 не может быть вертикальной асимптотой, если функция непрерывна в точке
не может быть вертикальной асимптотой, если функция непрерывна в точке 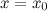 . Поэтому вертикальные асимптоты следует искать в точках разрыва функции.
. Поэтому вертикальные асимптоты следует искать в точках разрыва функции.
Определение
Прямая 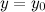 называется горизонтальной асимптотой графика функции
называется горизонтальной асимптотой графика функции 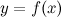 , если хотя бы одно из предельных значений
, если хотя бы одно из предельных значений 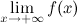 или
или 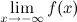 равно
равно 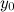 .
.
Замечание. График функции может иметь только правую горизонтальную асимптоту или только левую.
Определение
Прямая 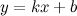 называется наклонной асимптотой графика функции
называется наклонной асимптотой графика функции 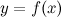 , если
, если 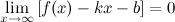
Нахождение наклонной асимптоты
Теорема
(условиях существования наклонной асимптоты)
Если для функции 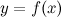 существуют пределы
существуют пределы 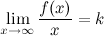 и
и 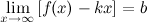 , то функция имеет наклонную асимптоту
, то функция имеет наклонную асимптоту 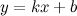 при
при  .
.
Замечание
Горизонтальная асимптота является частным случаем наклонной при 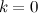 .
.
Замечание
Если при нахождении горизонтальной асимптоты получается, что 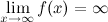 , то функция может иметь наклонную асимптоту.
, то функция может иметь наклонную асимптоту.
Замечание
Кривая 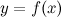 может пересекать свою асимптоту, причем неоднократно.
может пересекать свою асимптоту, причем неоднократно.
41)Определение производной. Геометрический смысл производной.
Производной  от функции
от функции 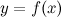 в точке
в точке 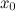 называется предел отношения приращения функции
называется предел отношения приращения функции 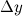 к приращению аргумента
к приращению аргумента 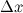 :
: 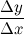 при
при 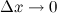 , если он существует, то есть:
, если он существует, то есть: 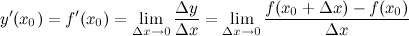
или
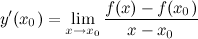
Геометрический смысл производной
Производная функции 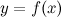 , вычисленная при заданном значении
, вычисленная при заданном значении  , равна тангенсу угла, образованного положительным направлением оси
, равна тангенсу угла, образованного положительным направлением оси 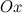 и положительным направлением касательной, проведенной к графику этой функции в точке с абсциссой
и положительным направлением касательной, проведенной к графику этой функции в точке с абсциссой  :
: 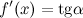
Замечание
Геометрически производная представляет собой угловой коэффициент касательной к графику функции 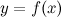 в точке
в точке 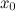 .
.
42)Теорема о непрерывности дифференцируемой функции.
Теорема. Если функция 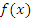 дифференцируема в некоторой точке a, то она непрерывна в этой точке.
дифференцируема в некоторой точке a, то она непрерывна в этой точке.
Доказательство. По определению производной
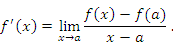
Это предельное равенство означает, что выражение под знаком предела можно представить в виде
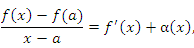
где α(x) – бесконечно малая функция при x → a. Тогда
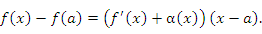
Следовательно, 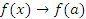 при x → a.
при x → a.
Заметим, что дифференцируемость функции в некоторой точке означает ее гладкость в окрестности этой точки, что влечет за собой непрерывность функции в рассматриваемой точке. Однако обратное утверждение несправедливо – функция, обладающая свойством непрерывности в некоторой точке, не обязательно дифференцируема в этой точке.
43)Производные степенной и показательной функции.
Степенно-показательной функцией (или показательно-степенной, или функцией в степени функция) называется функция вида 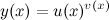
Рассмотрим способы нахождения ее производной.
1-ый способ
Применяя формулу:
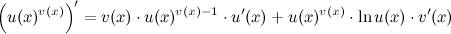
То есть вначале производная берется как от степенной функции, а потом как от показательной.
Замечание
Порядок следования слагаемых неважен: можно вначале взять производную от показательной функции, а затем как от степенной, так как от перестановки слагаемых сумма не меняется:
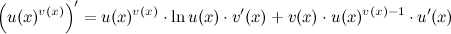
2-ой способ
С помощью логарифмического дифференцирования:
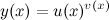
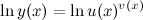
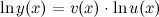
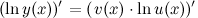
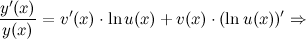
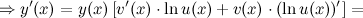
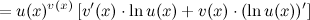
3-ий способ
Представим функцию 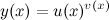 в следующем виде (используются свойства логарифмов):
в следующем виде (используются свойства логарифмов):
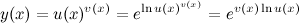
Тогда
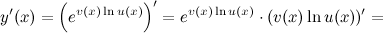
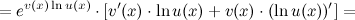
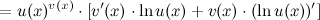
44)Производные тригонометрических функций.
| Производная | Область определения |
| (sinx)′=cosx | −∞<x<∞ |
| (cosx)′=−sinx | −∞<x<∞ |
| (tanx)′=1cos2x=sec2x | x≠π2+πn,n∈Z |
| (cotx)′=−1sin2x=−csc2x | x≠πn,n∈Z |
| (secx)′=tanxsecx | x≠π2+πn,n∈Z |
| (cscx)′=−cotxcscx | x≠πn,n∈Z |
| (arcsinx)′=1√1−x2 | −1<x<1 |
| (arccosx)′=−1√1−x2 | −1<x<1 |
| (arctanx)′=11+x2 | −∞<x<∞ |
| (arccot x)′=−11+x2 | −∞<x<∞ |
| (arcsec x)′=1|x|√x2−1 | x∈(−∞,−1)∪(1,∞) |
| (arccsc x)′=−1|x|√x2−1 | x∈(−∞,−1)∪(1,∞) |
45)Производная логарифмической функции. Логарифмическое дифференцирование.Производная показательно-степенной функции.(см.43)
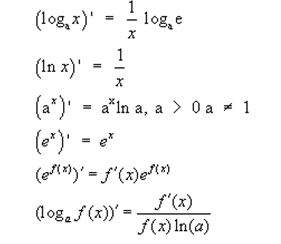
Для функций вида 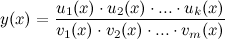 для упрощения нахождения производной рациональнее использовать логарифмическое дифференцирование.
для упрощения нахождения производной рациональнее использовать логарифмическое дифференцирование.
Суть метода логарифмического дифференцирования
Суть такого дифференцирования заключается в следующем: вначале находится логарифм заданной функции, а уже затем вычисляется от него производная. Пусть задана некоторая функция