ВВЕДЕНИЕ
Вектор (от лат. vector, «несущий») — в простейшем случае математический объект, характеризующийся величиной и направлением. Например, в геометрии и в естественных науках вектор есть направленный отрезок прямой в евклидовом пространстве (или на плоскости). Примеры: радиус-вектор, скорость, момент силы. Если в пространстве задана система координат, то вектор однозначно задаётся набором своих координат. Поэтому в математике, информатике и других науках упорядоченный набор чисел часто тоже называют вектором. В более общем смысле вектор в математике рассматривается как элемент некоторого векторного (линейного) пространства.
Вектор можно не только умножать на число, но и перемножать вектора между собой. Такое действие носит название скалярного произведения векторов. Если сложение или вычитание векторов является, в общем-то, достаточно понятным и логичным действием, которое просто отображается графически, то с пониманием скалярного произведения векторов не всё так просто. Гораздо легче запомнить формулу скалярного умножения двух векторов, она куда проще для запоминания, нежели для понимания.
ИСТОРИЧЕСКАЯ СПРАВКА
Многие историки считают «родителями векторного пространства» ирландского учёного XIX в. У. Гамильтона, а также его немецких коллег и современников Г. Грассмана. Даже сам термин «вектор» ввел также Гамильтон около 1845 г. Он же определил скалярное и векторное произведения векторов в 1853 году. Заметим, что эти произведения фигурировали в работах Грассмана еще в 1844 году. Он называл их внутренним и внешним произведениями. Однако работы Грассмана не были поняты и по достоинству оценены современниками.
Между тем историю векторного исчисления, как историю и корни всякой крупной математической теории, можно проследить задолго до его выделения в самостоятельный раздел математики. Так еще Архимед в его всем известном законе присутствует величина, характеризующаяся не только численным значением, но и направлением. Более того: векторный характер сил, скоростей и перемещений в пространстве был знаком многим ученым Античного времени, а «правило параллелограмма» сложения векторов было известно еще в IV в. Р. Х. математикам школы Аристотеля. Вектор обычно изображался отрезком с указанным на нем направлением, т.е. направленным отрезком.
Параллельно с исследованиями комплексных чисел в работах многих математиков XVII-XVIII в. в., занимавшихся геометрическими проблемами, можно увидеть нарастание потребности в некоем геометрическом исчислении, подобном численному (исчислению действительных чисел), но связанному с пространственной системой координат. Его в какой-то мере пытался создать еще Лейбниц, продумывая свою «универсальную арифметику», но, несмотря на гениальность и необычайную широту интересов, сделать это ему не удалось. Однако уже к концу XVIII в. отдельные идеи векторного исчисления, которое и стало тем исчислением, что искали геометры, смог сформулировать французский ученый Л. Карно. А в 30-х годах XIX в. у Гамильтона и Грассмана в работах по теории комплексных чисел и кватернионов эти идеи были сформулированы уже совершенно прозрачно, хотя, по существу, что удивительно, они имели дело только с некоторыми примерами тех конечномерных векторных пространств, которые теперь бы мы назвали – координатными.
Так называемые функциональные векторные пространства привлекли внимание математиков уже в начале нашего века рослее инновационных результатов в этой области итальянца С. Пинкерля и немецкого математика О. Теплица, который известен своими работами по теории матриц, и, в частности, тем, что придумал удачную общую модель векторного пространства – координатное векторное пространство. Именно Хевисайд ввел в 1891 г. одно из закрепившихся в научной литературе обозначающий вектора: а, автором двух других общепринятых ныне обозначений векторов: ā был Ж. Арган, а для обозначения свободного вектора предложил А. Мебиус. Термин «скалярный» в современном смысле впервые употребил У. Гамильтон в 1843 г. Так скалярное произведение начало применяться в математике для решения не только геометрических, но и алгебраических задач.
Чтобы рассмотреть дальнейшие понятия о векторах необходимо ввести понятие о векторном исчислении.
ВЕКТОРНОЕ ИСЧИСЛЕНИЕ
Векторное исчисление – раздел математики, в котором изучаются свойства операций над векторами.
В связи с разнообразием векторов, зависящих от пространства, в котором они исчисляются, векторное исчисление разделяется на:
· Векторную алгебру
· Векторный анализ
· Функциональный анализ
Рассмотрением векторного исчисления являются тензорные исчисления, изучающие тензоры и тензорные поля.
Векторная алгебра изучает свойства линейных операций с векторами: сложение, умножение на число, различные произведения – скалярное, псевдоскалярное, векторное, смешанное, двойное векторное и.т.д.
В аналитической и теоретической механике на базе законов векторной алгебры исследуется движение и взаимодействие материальных тел.
Векторный анализ – раздел векторного исчисления, который исследует статистические, стационарные и динамические, векторные и скалярные поля. Векторный анализ оперирует с понятиями поток вектора, циркуляция вектора. Оперируя данными понятиями исследуется взаимоотношение определяющих поля скаляров и векторов и доказываются базовые теоремы.
Функциональный анализ - это раздел анализа, в котором изучаются бесконечные топологические векторные пространства и их отображения. Это пространство функций, теория мера и интеграла, теория функций, теория операторов, дифференциальное исчисление.
Функциональный анализ широко применяется в теории дифференциальных уравнений, математической физики, теоретической физики, квантовой механике.
В своем проекте я рассматриваю скалярное произведение.
СКАЛЯРНОЕ ПРОИЗВЕДЕНИЕ
Для понятия свойства векторного исчисления, такого как скалярное произведение, необходимо ввести важные понятия.
3.1 Вектор
Вектор – это направленный отрезок прямой, то есть отрезок, для которого указано какая из его граничных точек является началом, а какая концом.
Вектор может обозначаться как 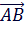 ,
, 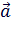 .
.
3.2 Координаты вектора
Координаты определяются как разность точек координат его начала и его конца. Например на координатной плоскости, если даны координаты точек начала и конца вектора 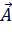 =(x1,y1) и
=(x1,y1) и 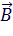 =(x2,y2), то координаты вектора
=(x2,y2), то координаты вектора 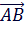 будут:
будут:
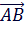 =
= 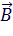 -
- 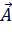 =(x2y2)-(x1y1)
=(x2y2)-(x1y1)
3.3 Длина вектора
Длина вектора– это расстояние между двумя точками A и B, ее обычно обозначают
|AB|=|B-A|=|(x2-x1,y2-y1)|= √(x2-x1)2 + (y2-y1)2
3.4 Нулевой вектор
Нулевой вектор – это вектор, у которого начало и конец совпадают, то есть у него нет направления. A(x1,y1)=B(x1,y1)
3.5 Угол между векторами
Два вектора 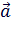 и
и 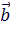 всегда образуют между собой угол, который обозначается:
всегда образуют между собой угол, который обозначается: 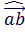
Он может принимать значения от 0° до 180° включительно.
Если векторы не параллельны, то их можно расположить на пересекающихся прямых.
Векторы могут образовать:
1. острый угол;
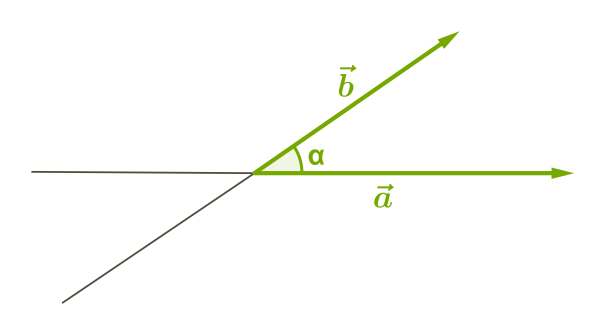
Рисунок 1
2. тупой угол
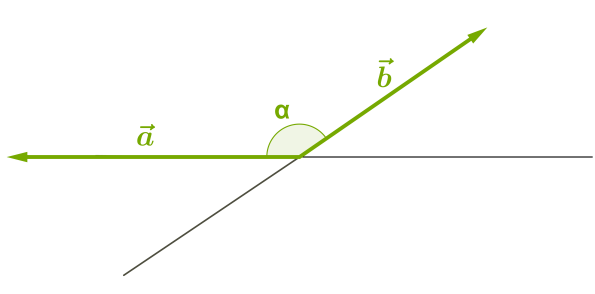
Рисунок 2
3. прямой угол (векторы перпендикулярны)
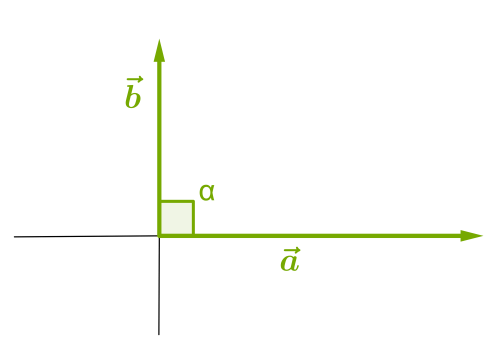
Рисунок 3
Если векторы расположены на параллельных прямых, то они могут образовать:
4. угол величиной 0° (векторы сонаправлены);
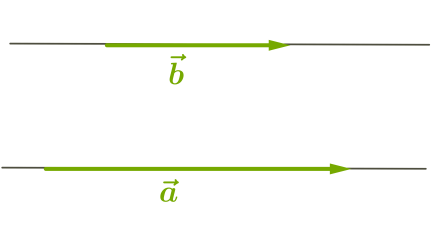
Рисунок 4
5. угол величиной 180° (векторы противоположно направлены).
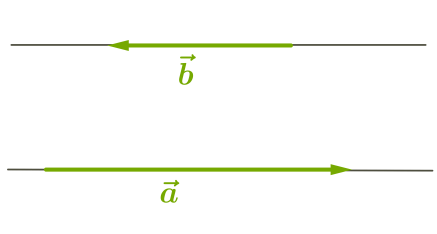
Рисунок 5
Если один из векторов или оба вектора нулевые, то угол между ними будет равен 0°.
3.6 Проекция векторов
Для координатного представления векторов большое значение имеет понятие проекция вектора на ось (направленную прямую-l)
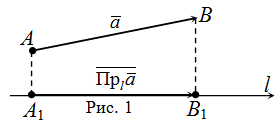
Рисунок 6
Если направленная проекция AB совпадает по направлению с осью l, то проекция положительна и наоборот.
|Прla|=|a| cos a,l
Если вектор и ось между собой перпендикулярны то проекция = 0
3.7 Виды векторов
Виды векторов: свободные скользящие и фиксированные вектора.
· Свободные вектора
Свободные вектора– это любые векторы имеющие одинаковое направление и длину. Свободные векторы AC и BD равны, если найдутся точки E и F, такие что четырехугольники ABFE и CDFE – параллелограммы.
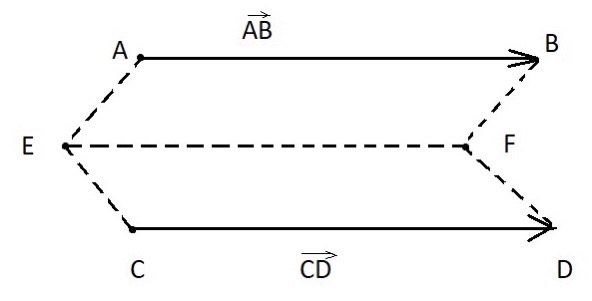
Рисунок 7
· Скользящие вектора
Говоря о скользящий векторах добавляем что начала равных скользящих векторов должны совпадать или лежать на одной прямой, на которой лежат изображающие эти векторы направленные отрезки (так что один может быть совмещен с другим перемещением в направлении им же заданным).Даны скользящие вектора AC и CD они равны если точки A,B,C,D лежат на одной прямой S и |AB| = |CD|

Рисунок 8
· Фиксированные вектора
Говоря о фиксированных векторах-говорят, что равными считаются только векторы, у которых совпадают и направления и начала (то есть в этом случае нет двух фиксированных векторов с различными началами, которые считались бы равными)
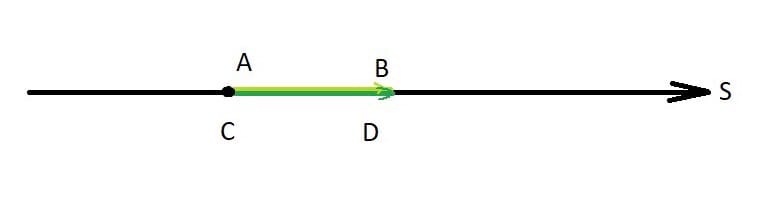
Рисунок 9
3.8 Отношения между векторами
· Коллинеарные вектора
Два вектора называются коллинеарными если они лежат на параллельных прямых, либо на одной прямой
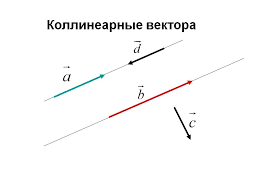
Рисунок 10
· Сонаправленные вектора
Два вектора называются сонаправленными, если они коллинеарные и направлены в одну сторону
· Противоположно направленные вектора
Противоположно направленные вектора коллинеарные и направлены в разные стороны
· Компланарные вектора
Три вектора называются компланарными если они будучи приведенными к общему началу лежат в одной плоскости.
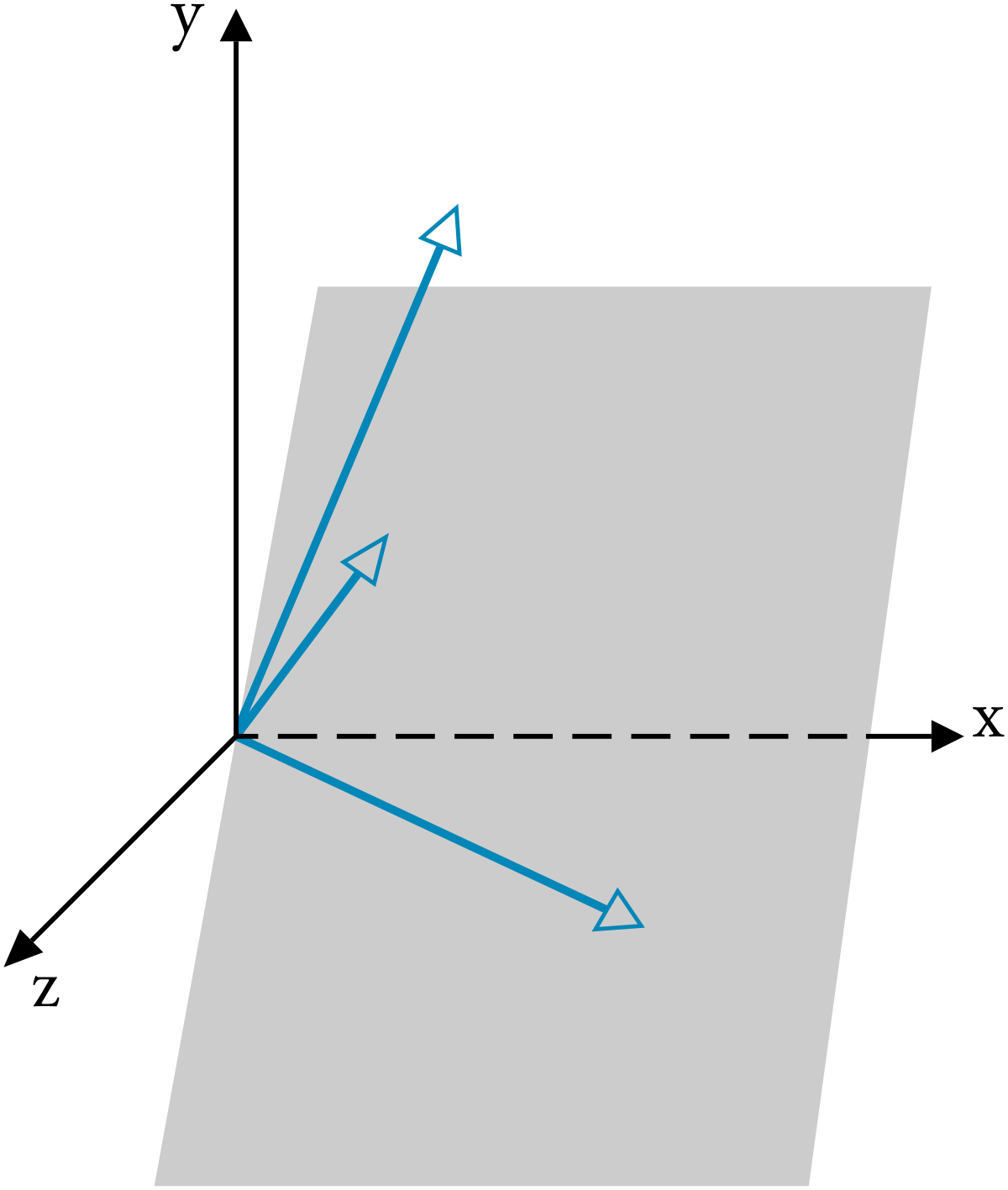
Рисунок 11
3.9 Определение скалярного произведения
Определение 1: Скалярным произведением двух векторов называется число, равное произведению длин этих векторов на косинус угла между ними. Если один из векторов нулевой скалярное произведение считается равным нулю.
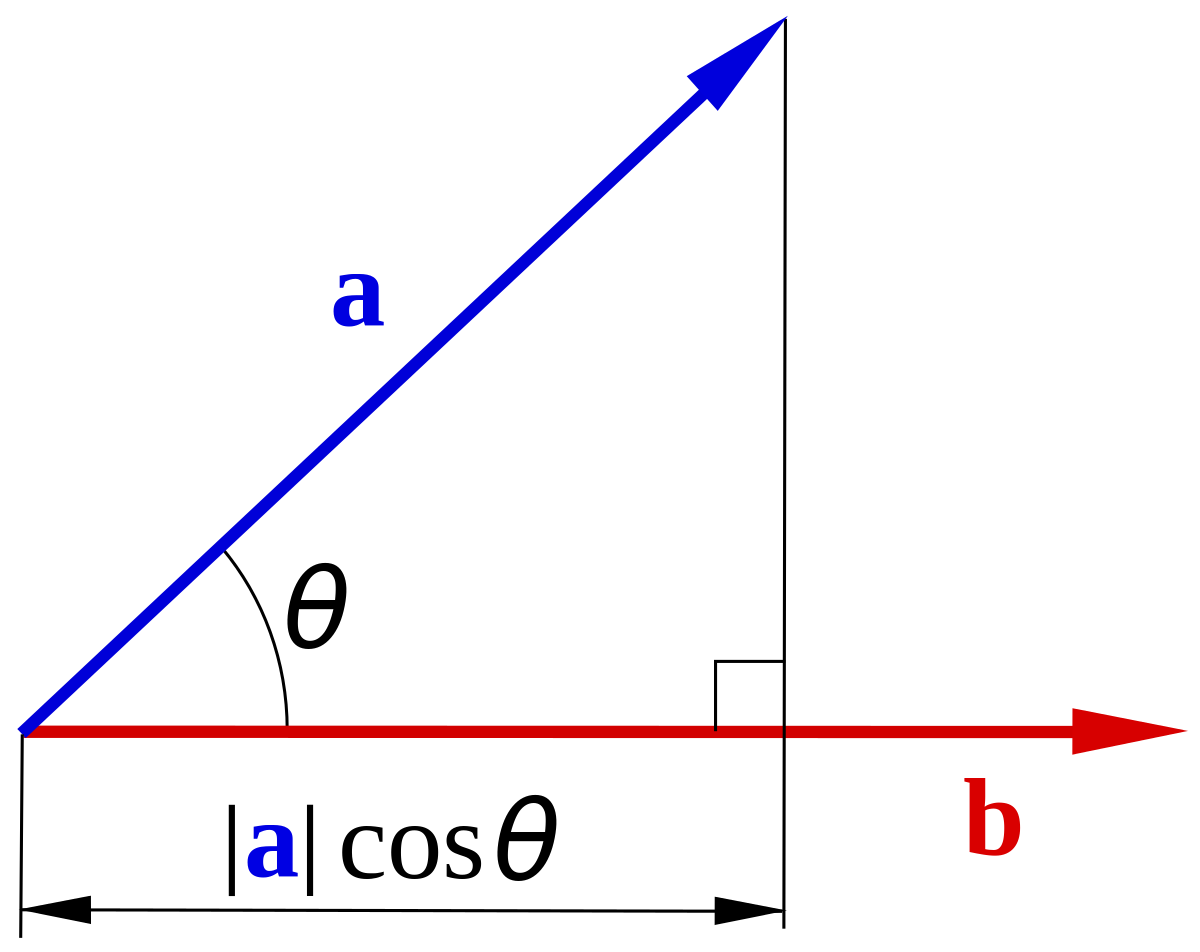
Рисунок 12
(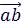 )=|a| |b| cos θ
)=|a| |b| cos θ
Определение 2: Скалярным произведением двух векторов 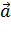 и
и 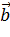 называется произведение длины вектора
называется произведение длины вектора 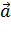 на числовую проекцию вектора
на числовую проекцию вектора 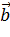 на направление вектора
на направление вектора 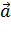 или произведение длины вектора
или произведение длины вектора 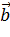 на числовую проекцию вектора
на числовую проекцию вектора 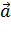 на направление вектора
на направление вектора 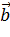 .
.
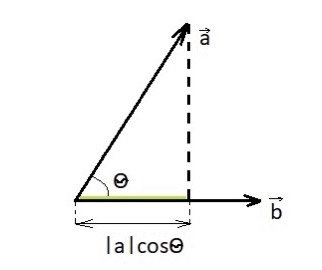
Рисунок 13
(ab) = | 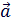 ||
|| 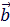 |cosθ = |
|cosθ = | 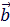 |*Прb
|*Прb 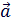
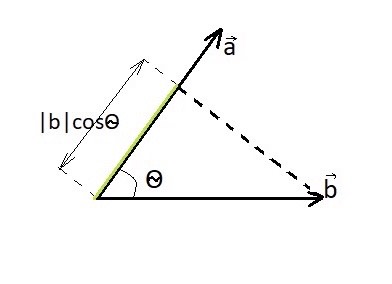
Рисунок 14
| 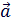 ||
|| 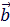 |cosθ = |
|cosθ = | 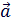 |*Прa
|*Прa 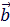
Определение 3: Скалярным произведением двух векторов на плоскости или в трехмерном пространстве в прямоугольной системе координат называется сумма произведений соответствующих координат векторов 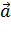 и
и 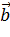 .
.
3.10 Формулы скалярного произведения заданных координатами
1. Формула скалярного произведения векторов для плоских задач:
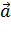 =(ax,ay) и
=(ax,ay) и 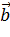 =(bx,by)
=(bx,by)
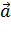 *
* 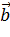 =ax*bx+bx*by
=ax*bx+bx*by
2. Формула скалярных координат векторов для пространственных задач
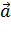 =(ax,ay,az ) и
=(ax,ay,az ) и 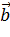 =(bx,by,bz)
=(bx,by,bz)
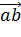 = ax*bx + ay*by + az*bz
= ax*bx + ay*by + az*bz
3. Формула скалярного произведения векторов для n-мерных векторов
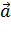 =(a1,a2,….an)
=(a1,a2,….an) 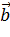 =(b1,b2,….bn)
=(b1,b2,….bn)
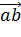 =a1*b1+a2*b2+…..+an*bn
=a1*b1+a2*b2+…..+an*bn
3.11Свойства скалярного произведения
1. Скалярное произведение вектора самого на себя всегда больше 0 или больше 0:
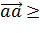 0
0
2. Скалярное произведение вектора самого на себя равно 0, когда 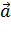 =0
=0
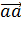 =0
=0
3. Скалярное произведение вектора самого на себя равно квадрату его модуля и называется скалярный квадрат:
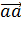 =
= 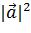
4. Операция скалярного умножения коммутативна. Переместительный закон:
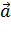 *
* 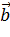 =
= 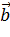 *
* 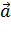
5. Если скалярное произведение двух ненулевых векторов равно 0, то эти вектора ортогональны (перпендикулярны):
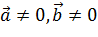 ,
, 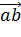 =0
=0 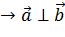
6. Ассоциативный (сочетательный) закон:
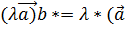 *
* 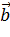 )
)
7. Операция скалярного произведения дистрибутивна. Распределительный закон:
(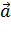 +
+ 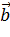 )*
)* 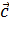 =
= 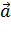 *
* 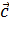 +
+ 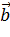 *
* 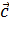
ПРИМЕНЕНИЕ СКАЛЯРНОГО ПРОИЗВЕДЕНИЯ НА ПРАКТИКЕ
Векторы имеют широкое применение в геометрии и прикладных науках, где используются для представления величин, имеющих направление (сила, скорость и т п). Применение векторов упрощает ряд операций, например, определение углов между прямыми или отрезками, вычисление площадей фигур. Использование векторов может быть положено в основу метода координат.
Пример 1.
Найти скалярное произведение векторов a и b, если |a|=3, |b|=6, 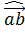 =
= 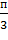 .
.
Решение:
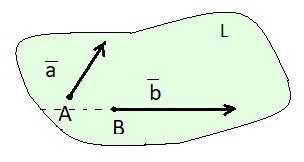
Рисунок 15
1)Берем точку С, совмещаем точки A и B в точке C.
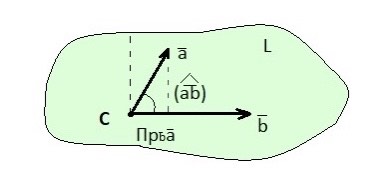
Рисунок 16
2)Согласно определению скалярного произведения имеем
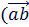 ) = |
) = | 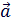 |* |
|* | 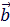 |* cos
|* cos 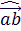 = |
= | 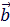 |* |
|* | 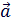 |* cos
|* cos 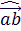 = |
= | 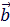 |* Прa
|* Прa 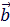 = 6*3*cos
= 6*3*cos  = 6*3*
= 6*3*  = 9
= 9
Пример 2.
Дано:  ,
, 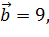 (
(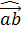 ) = 135
) = 135 
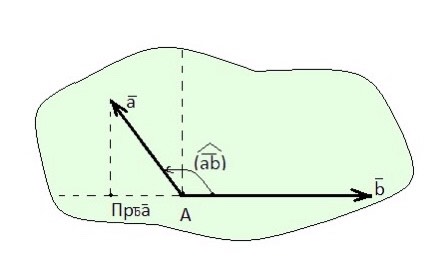
Рисунок 17
Найти: 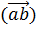
Решение: 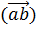 =
= 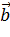 *
* 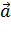 * cos
* cos 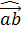 = 9*4*cos135 = 9*4*(-
= 9*4*cos135 = 9*4*(- 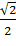 ) =
) = 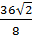 = -18
= -18 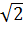
Таким образом знак скалярного произведения зависит от (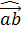 ).
).
Если 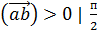 > (
> (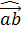 ) > 0
) > 0
и 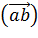 < 0 | П > (
< 0 | П > (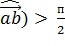
и 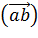 = 0 | (
= 0 | (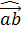 ) =
) = 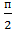 то есть
то есть 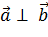
Пример 3.
Скалярное произведение имеет физический смысл. Например, в механике. Если рассматривать перемещение какого-то предмета из одной точки в другую под действием какой-то силы в определенном направлении на определенное расстояние, можно определить совершаемую работу. Или наоборот.
Определить совершаемую работу A при перемещении тележки с силой F=3 Ньютона приложенной под углом 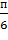 на расстояние 6 м.
на расстояние 6 м.
Решение: | 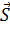 | = 6*(
| = 6*(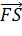 ) =
) = 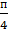 : 3*6cos(
: 3*6cos(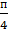 ) =
) = 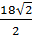
A = (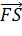 ) =
) = 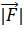 *|
*| 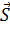 |*cos
|*cos 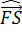 = 3*6*cos30
= 3*6*cos30  = 18*
= 18* 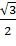 = 9
= 9 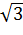 Джоуля
Джоуля
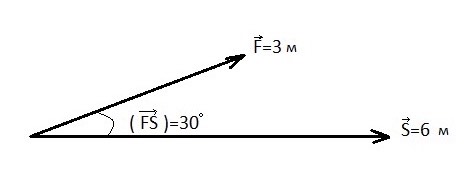
Рисунок 18
Подобным образом можно решать и обратные задачи. То есть определить длину перемещения и приложенную силу, зная совершаемую работу.
Пример 4.
Скалярное произведение в экономике
Предполагаем, что в магазине продается товар различных видов, характеризующийся различными качествами. Весь товар можно изобразить неким вектором 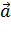 (50,75,100). Стоимость этих товаров отображается соответственно неким вектором
(50,75,100). Стоимость этих товаров отображается соответственно неким вектором 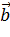 (4,5,7). Эти вектора коллинеарные, так как
(4,5,7). Эти вектора коллинеарные, так как 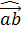 =0.Тогда скалярное произведение
=0.Тогда скалярное произведение 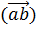 =50*4+75*5+100*7=200+375+700=1275
=50*4+75*5+100*7=200+375+700=1275
Пример 5.
Скалярное произведение в авиации.
Предполагаем, что самолет развивает тяговую силу 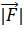 = 10000 кг и взлетает под углом 30
= 10000 кг и взлетает под углом 30  . Определить какой длины S должна быть взлетная полоса, если работа совершенная им (
. Определить какой длины S должна быть взлетная полоса, если работа совершенная им (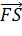 )=2000000 кгм.
)=2000000 кгм.
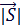 =
= 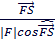 =
= 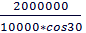 =
= 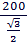 =
= 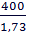 = 231 м
= 231 м
Пример 6.
Предполагается, что тяговая сила двигателя самолета составляет 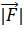 =12000 кг. Какую работу самолет совершит, взлетая под углом
=12000 кг. Какую работу самолет совершит, взлетая под углом 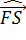 = 45
= 45  на расстояние
на расстояние 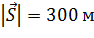
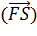 =
= 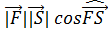 =12000 *300*cos45
=12000 *300*cos45 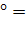 3600000
3600000 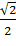 =1800000
=1800000 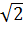 кгм =253800 кгм
кгм =253800 кгм
Пример 7
Какой должна быть тяговая сила 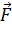 двигателя самолета при взлете его на расстояние
двигателя самолета при взлете его на расстояние 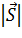 =500м под углом 30
=500м под углом 30  , если при этом он совершает работу A=1600000 кгм.
, если при этом он совершает работу A=1600000 кгм.
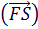 =
= 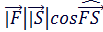
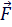 =
= 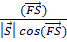 =
= 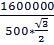 =
= 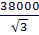 =
= 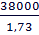 = 21965 кг.
= 21965 кг.
Пример 8.
Под каким углом взлетает самолет, если тяговая сила его двигателя 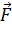 = 12000 кг, а длина взлетной полосы составляет
= 12000 кг, а длина взлетной полосы составляет 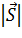 =400м, при этом он совершает работу A=1600000 кгм
=400м, при этом он совершает работу A=1600000 кгм
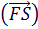 =
= 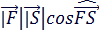 =
= 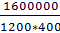 =
=  = 0,33. Это
= 0,33. Это 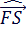 =71
=71  , что невозможно.
, что невозможно.
Пример 9.
Чтобы самолет взлетел необходимо увеличить тяговую силу 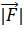 =25000 кг, при этом и работа совершенная двигателем на расстоянии
=25000 кг, при этом и работа совершенная двигателем на расстоянии 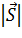 = 400 м также увеличится. A=
= 400 м также увеличится. A= 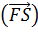 =
= 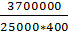 =
= 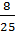 =0,56
=0,56
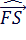 = 56
= 56  . Возможно.
. Возможно.
ЗАКЛЮЧЕНИЕ
Как видим из рассмотренных примеров скалярное произведение широко применяется во многих областях жизнедеятельности человека. Что способствует развитию и совершенствованию различных технологических процессов.
И в целом глубокие знания векторного исчисления позволяют широко применять этот раздел математики в изучении различных процессов в природе деятельности человека.