Сумма коэффициентов, кроме первого и второго, сокращённых на P
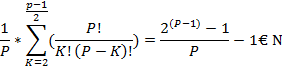
(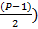 +(
+(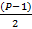 *
* 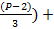 ...
...  (
(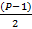 *
* 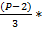 ...
... 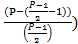 =
= 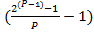 ? N
? N
В зависимости от количества уникальных биномиальных коэффициентов 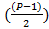 , количество элементов, оказывающих влияние на итоговый результат проверки числа на простоту, растёт. Количество которых равно, количеству уникальных биномиальных коэффициентов
, количество элементов, оказывающих влияние на итоговый результат проверки числа на простоту, растёт. Количество которых равно, количеству уникальных биномиальных коэффициентов 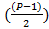
1+(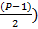 +(
+(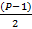 *
* 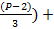 ...
...  (
(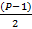 *
* 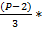 ...
... 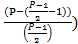 =
= 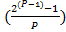 ? N
? N
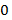 =
= 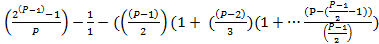
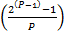 –
– 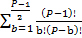 = 0
= 0 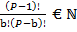
Т.е. Количество элементов, переносимых в правую часть уравнения, для сохранения истинности теста простоты, равняется 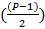 .
.
Рассмотрим несколько простых чисел P=3;5
Для P=3
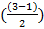 =1
=1
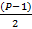 *
* 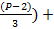 ...
...  (
(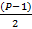 *
* 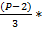 ...
... 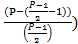 =
= 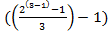 = 0
= 0
Для P=5
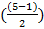 =2
=2
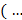 (
(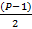 *
* 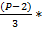 ...
... 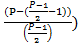 =
= 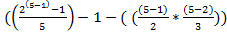 = 0
= 0
Зная число вычитаемых элементов, для обнуления уравнения, найдем (P(п)) - число проходящее тест простоты
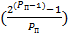 =
= 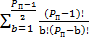
Поскольку количество вычитаемых элементов равно, количеству уникальных биномиальных коэффициентов, перепишем формулу.
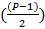 = b
= b
2b + 1=P(п)
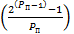 =
= 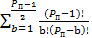 =1+(
=1+(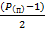 ) + (
) + (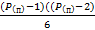 ) +…
) +…
Выведем формулу максимального значения уникального коэффициента. Где b – порядковый номер, исследуемого, потенциального простого числа. Где q – порядковый номер, исследуемого, коэффициента, за исключением единицы (Счёт идёт от коэффициента стоящего при меньшей степени).
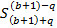 =
= 
Найдём сумму всех уникальных коэффициентов.
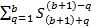 =
= 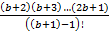 +
+ 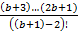 ...+
...+ 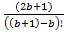
Разделим сумму, всех уникальных коэффициентов, за исключением единицы, на второй коэффициент.
 =
= 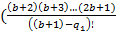 +
+ 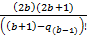 ...+
...+ 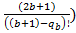 /
/ 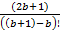
Исходя из правила деления дробей, перепишем формулу.
 =
= 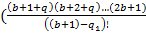 +
+ 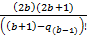 ...+
...+ 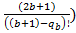 *
* 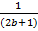
Для удобства, разделим каждый коэффициент на второй обособленно, лишь затем сложим результаты.
Отношение третьего коэффициента ко второму.
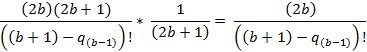
Отношение четвертого коэффициента ко второму.
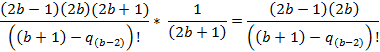
Отношение максимального коэффициента ко второму.
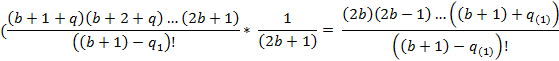
На данном этапе видно, что для некоторых b, порядковых номеров потенциального простого числа, не существует целого решения. Но при этом, сумма всех коэффициентов,
для b, порядковый номер, скрывающий за собой псевдо-простое число, такое решение имеется, в силу взаимной компенсации дробных частей.
Выведем общую формулу сумм отношений уникальных коэффициентов, за исключением первого.
 =
= 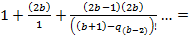
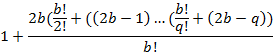
Определим количество b, порядковых номеров потенциального простого числа, для которых не существует целого решения.
Для этого на понадобится: 1) теорема Безу: Остаток r от деления многочлена P(x) на двучлен (x ‑ a) равен значению этого многочлена в точке a, т.е. r = P(a). 2) тест AKS
X=2b+1
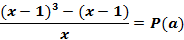
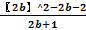 =
= 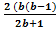 =
= 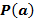
Сейчас я покажу вам силу математики.
Двоичный код числа = N
| N | B=(N-1)/2 если да 1, если нет 0 |
Сравне́ние двух целых чисел по мо́дулю натурального числа m {\displaystyle m} — математическая операция, позволяющая ответить на вопрос о том, дают ли два выбранных целых числа при делении на m {\displaystyle m} один и тот же остаток. Любое целое число при делении на m {\displaystyle m} дает один из m {\displaystyle m} возможных остатков: число от 0 до m − 1 {\displaystyle m-1}; это значит, что все целые числа можно разделить на m {\displaystyle m} групп, каждая из которых отвечает определённому остатку от деления на m {\displaystyle m}.
Арифметические операции с остатками чисел по фиксированному модулю образуют мо́дульную арифме́тику или модуля́рную арифметику [1][2], которая широко применяется в математике, информатике и криптографии[3].
(2p-1-1) mod (p) = P(a)
P(a) = 2 = Z
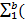 (N-1) mod (2)) = 1 V 2 = XY
(N-1) mod (2)) = 1 V 2 = XY
Если P(a) = 2 = Z, а 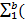 (N-1) mod (2)) = 1 V 2 = XY, то вместе.
(N-1) mod (2)) = 1 V 2 = XY, то вместе.
XY 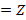 То простое, если нет Тоо составное
То простое, если нет Тоо составное
XY 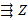 Если да то простое, если нет то составное.
Если да то простое, если нет то составное.
d – порядковый номер числа
| N | Pп=b+1 | Уровень проверки | 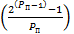 = = 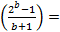 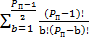
| b= |
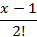
| 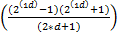
| 2d | ||
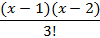
| 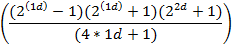
| 4d | ||
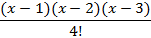
| 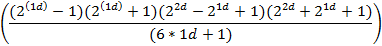
| 6d | ||
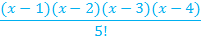
| 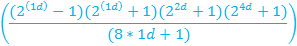
| 8d | ||
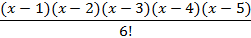
| 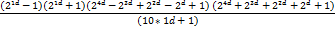
| 10d | ||
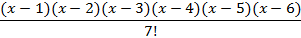
| 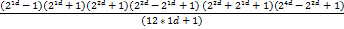
| 12d | ||
| 340d |
P(п)= 3
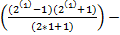
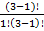 =
= 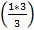 -1=0
-1=0
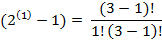
P(п)=5
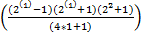 -
- 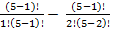 =
= 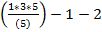 =0
=0
P(п)=7
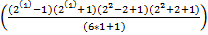 -
- 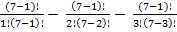 =
= 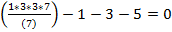
P(п)=9
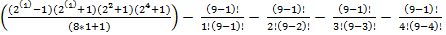 =
= 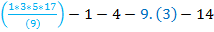
P(п)=11
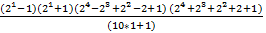 -
- 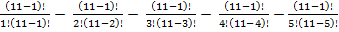 =
= 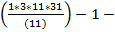 5 -15 -30-42=0
5 -15 -30-42=0
P(п)=13
(21-1)(21+1)(22+1)(22-2+1) (22+2+1)(24-22+1) - 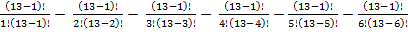 =
=
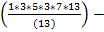 1-6-22-55-99-132=0
1-6-22-55-99-132=0
Вывод: все поставленные задачи были решены в ходе данной работы.
Примечание:
Фс – точность вычисления, количества чисел не удовлетворяющих малой теореме Ферма, на интервале от 1 до N, может быть повышена до абсолютной.
Вычисление Pф – может быть существенно облегчено, путём взаимного сокращения, частного и делителя
Список литературы и интернет источников:
https://ru.wikipedia.org/wiki/%D0%A2%D0%B5%D1%81%D1%82_%D0%90%D0%B3%D1%80%D0%B0%D0%B2%D0%B0%D0%BB%D0%B0_%E2%80%94_%D0%9A%D0%B0%D1%8F%D0%BB%D0%B0_%E2%80%94_%D0%A1%D0%B0%D0%BA%D1%81%D0%B5%D0%BD%D1%8B
https://ru.wikipedia.org/wiki/%D0%91%D0%B8%D0%BD%D0%BE%D0%BC_%D0%9D%D1%8C%D1%8E%D1%82%D0%BE%D0%BD%D0%B0
https://ru.wikipedia.org/wiki/%D0%9C%D0%B0%D0%BB%D0%B0%D1%8F_%D1%82%D0%B5%D0%BE%D1%80%D0%B5%D0%BC%D0%B0_%D0%A4%D0%B5%D1%80%D0%BC%D0%B0