Производная сложной функции

Из примера видно, что сложная функция это функция от функции. Следовательно, можно дать следующее определение сложной функции:

Определение: Функция вида

y = f(g(x))

называется сложной функцией, составленной из функ­ций f u g, или суперпозицией функцийf и g.

Пример: Функция у =ln( cos x) есть сложная функция, составленная из функций

у = lnu и u = cos x.

Поэтому сложную функцию часто пишут в виде

y = f(u), где u = g(x).

Внешняя функция Промежуточная

функция

При этом аргумент х называют независимой перемен­ной, а u - промежуточным аргументом.

Вернемся к примеру. Производную каждой из этих функций мы можем вычислить, используя таблицу производных.

Как же вычислить производную сложной функции?

Ответ на этот вопрос дает следующая теорема.

Теорема: Если функция u = g(x) дифференци­руема в некоторой точке х ₀, а функция y=f(u) дифференцируема в точке u₀ = g(x₀), то сложная функция у=f(g(x)) дифференцируема в данной точке x₀.

При этом

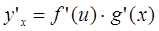
или

,

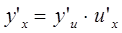т.е. производная от у по переменной х равна производной от у по переменной и, умноженной на производную о т и по переменной х.

Правило:

1 Чтобы найти производную сложной функции, надо ее правильно прочитать;

2 Чтобы правильно прочитать функцию, надо определить в ней порядок действий;

3 Функцию читаем в обратном порядку действий направлении;

4 Производную находим по ходу чтения функции.

А теперь разберем это на примере:

Пример1: Функция у =ln( cos x) получается последовательным выполнением двух операций: взятия косинуса угла х и нахождения от этого числа натурального логарифма:

.

Функция читается так: логарифмическая функция от тригонометрической функции.

Продифференцируем функцию: у =ln( cos x)=lnu, u=cosx.

.

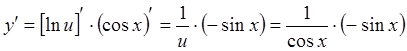На практике такое дифференцирование производится гораздо короче и проще, во всяком случае, без введения записи и.

Искусство дифференцирования сложной функции заключается в умении видеть в момент дифференцирования только одну функцию (именно - дифференцируемую в данный момент), не замечая пока другие, откладывая их видение до момента дифференцирования.

Будем использовать при дифференцировании дополненную таблицу производных.

.

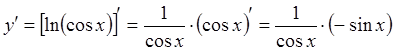Пример2: Найти производную функции у = (x³ - 5х + 7)⁹.

Решение: Обозначив в «уме» u = х³ – 5x +7, получим у = u⁹. Найдем:

и

По формуле имеем

Дифференцирование функций, заданных параметрически

Если функция y = f(x) задана в виде:

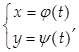
причем функция j(t) имеет обратную функцию t = Φ(x), то у = y(Φ(х)), и

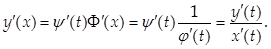
Полученная формула дает возможность находить производную функции, заданной параметрически, без определения непосредственной зависимости у от х.

Пример.

х = а(1 – cost), y = a(t– sint) – параметрические уравнения кривой, называемой циклоидой. Найдему΄(х):

Логарифмическое дифференцирование

Иногда полезно использовать так называемую формулу логарифмического дифференцирования. Пусть f(x)>0 на некотором множестве значений аргумента и дифференцируема на этом множестве. Тогда по формуле производной сложной функции

откуда

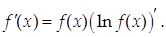
Эту формулу удобно использовать в тех случаях, когда производную натурального логарифма данной функции найти проще, чем производную самой функции.

Примеры.