В 1878 г. Немецкий математик Г. Фробениус доказал следующую замечательную теорему.
Теорема Фробениуса. Любая ассоциативная алгебра с делением изоморфна одной из трех: алгебре действительных чисел, алгебре комплексных чисел или алгебре кватернионов.
Впоследствии был установлен более общий результат, который можно назвать обобщенной теоремой Фробениуса.
Обобщенная теорема Фробениуса. Любая альтернативная алгебра с делением изоморфна одной из четырех алгебр: алгебре действительных чисел, алгебре комплексных чисел, алгебре кватернионов или алгебре октав.
Альтернативной алгеброй называется алгебра, в которой для любых двух элементов a, b справедливы равенства 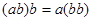 ,
, 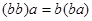 .
.
Чтобы доказать эти теоремы, перечислим сначала некоторые свойства ассоциативной алгебры с делением.
Утверждение 1. Алгебра А содержит 1.
Утверждение 2. Если элемент  не пропорционален 1, то совокупность
не пропорционален 1, то совокупность 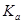 элементов вида
элементов вида 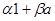 образует подалгебру, изоморфную алгебре комплексных чисел.
образует подалгебру, изоморфную алгебре комплексных чисел.
Утверждение 3. Если элементы  не принадлежат одной подалгебре
не принадлежат одной подалгебре  , то совокупность
, то совокупность 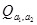 элементов вида
элементов вида  образует подалгебру, изоморфную алгебре кватернионов.
образует подалгебру, изоморфную алгебре кватернионов.
Доказательство теоремы Фробениуса.
Дадим сначала другое определение альтернативной алгебры.
Пусть a, b –два произвольных элемента алгебра А. Рассмотрим всевозможные произведения, составленные из них. Если каждое такое произведение не зависит от способа расстановки скобок, алгебра А называется альтернативной.
При доказательстве теоремы будем использовать второе определение альтернативности, т.е. докажем следующую теорему: Если алгебра А с делением такова, что любое произведение, составленное из двух произвольных элементов a, b, не зависит от расстановки скобок, то алгебра А изоморфна одной из четырех алгебр: алгебре действительных чисел, алгебре комплексных чисел, алгебре кватернионов или алгебре октав.
Доказательство утверждения 1. Найдя элемент е из уравнения xa=a и умножив обе части равенства ea=a слева на е, получим e(ea)=ea или, учитывая ее альтернативность, (ee)a=ea. Отсюда следует, что ее=е. Опять-таки в силу альтернативности имеем (be)e=b(ee) и e(ec)=(ee)c, т.е. (be)e=be и e(ec)=ec. Отсюда следует be=b и ec=c. Значит е - единица алгебры.
Другие утверждения примем без доказательства.
Попытаемся доказать, что алгебра А является нормированной. Отсюда по теореме Гурвица будет следовать нужный нам результат.
Введем в алгебре А операцию сопряжения следующим образом. Если элемент а пропорционален 1, то 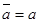 . Если же а не пропорционален 1, то, согласно утверждению 2, он содержится в комплексной подалгебре
. Если же а не пропорционален 1, то, согласно утверждению 2, он содержится в комплексной подалгебре  . В этой подалгебре для элемента а имеется сопряженный элемент
. В этой подалгебре для элемента а имеется сопряженный элемент  , который мы и примем за элемент, сопряженный к а в алгебре А.
, который мы и примем за элемент, сопряженный к а в алгебре А.
Из определения  непосредственно вытекает
непосредственно вытекает  , а также
, а также 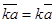 , где
, где  - любое.
- любое.
Для вывода других свойств сопряжения нам необходимо выяснить один вопрос. Пусть элемент а не пропорционален 1. Рассмотрим какую-либо кватернионную подалгебру  , содержащую а. В этой подалгебре для а тоже имеется сопряженный элемент
, содержащую а. В этой подалгебре для а тоже имеется сопряженный элемент  . Будет ли он совпадать с определенным выше элементом
. Будет ли он совпадать с определенным выше элементом 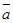 ? Покажем, что будет.
? Покажем, что будет.
Элементы а и  , как сопряженные в комплексной алгебре, удовлетворяют условиям
, как сопряженные в комплексной алгебре, удовлетворяют условиям 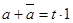 и
и  , где t, p – действительные числа.
, где t, p – действительные числа.
Элементы а и  как сопряженные в алгебре кватернионов удовлетворяют аналогичным условиям:
как сопряженные в алгебре кватернионов удовлетворяют аналогичным условиям:  и
и  , где k, l – действительные числа.
, где k, l – действительные числа.
Вычтем из последних равенств предыдущие, получим: 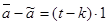 и
и 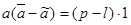 и если
и если 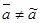 , то из этих соотношений вытекает, что элемент а пропорционален 1, что противоречит предположению.
, то из этих соотношений вытекает, что элемент а пропорционален 1, что противоречит предположению.
Т.о., элемент, сопряженный а, один и тот же, независимо от того, рассматриваем ли мы а как элемент комплексной подалгебры  (т.е. как комплексное число) или же как элемент какой-либо подалгебры
(т.е. как комплексное число) или же как элемент какой-либо подалгебры  (т.е. как кватернион).
(т.е. как кватернион).
Заметим попутно, что то же самое относится и к модулю элемента а. Поскольку 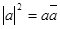 как в случае комплексных чисел, так и в случае кватернионов, то модуль элемента а не зависит от ого, рассматриваем ли мы а как элемент комплексной или же кватернионной подалгебры.
как в случае комплексных чисел, так и в случае кватернионов, то модуль элемента а не зависит от ого, рассматриваем ли мы а как элемент комплексной или же кватернионной подалгебры.
Из того, что доказано нами относительно сопряжения, легко следует, что для любых двух элементов a и b алгебры А справедливы равенства
 ,
, 
Действительно, если a и b принадлежат одной комплексной подалгебре (т.е.  совпадает с
совпадает с  ), то написанные равенства суть свойства сопряжения в этой подалгебре; если же b не содержится в
), то написанные равенства суть свойства сопряжения в этой подалгебре; если же b не содержится в  , то эти равенства снова справедливы – уже как свойства сопряжения в
, то эти равенства снова справедливы – уже как свойства сопряжения в 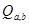 .
.
Из  и из
и из  вытекает, что элемент, сопряженный
вытекает, что элемент, сопряженный  равен
равен  ; следовательно,
; следовательно, 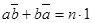 , n – действительное число.
, n – действительное число.
Определим в алгебре А скалярное произведение (a, b) с помощью формулы  . Что выражение (a, b) обладает всеми свойствами скалярного произведения, проверяется просто. Напомним эти свойства:
. Что выражение (a, b) обладает всеми свойствами скалярного произведения, проверяется просто. Напомним эти свойства:
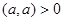 , если
, если  и (0,0)=0
и (0,0)=0


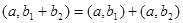
В данном случае свойство 2 очевидно, 2-е свойство вытекает из  , 3-е из
, 3-е из  . Для доказательства 1-го свойства следует написать
. Для доказательства 1-го свойства следует написать


и учесть, что модуль комплексного числа а строго положителен, если  , и равен нулю, если а=0.
, и равен нулю, если а=0.
Заметим, что из последнего равенства следует 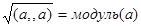 , т.е. норма элемента а в алгебре А совпадает с модулем а как комплексного числа (или кватерниона).
, т.е. норма элемента а в алгебре А совпадает с модулем а как комплексного числа (или кватерниона).
Т.к. любые 2 элемента a и b алгебры А принадлежат одной комплексной или одной кватернионной подалгебре, то 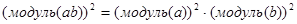 (ведь алгебра комплексных чисел, так же как и алгебра кватернионов, является нормированной), или (ab,ab)=(a,a)(b,b). Но это равенство как раз и означает нормированность алгебры А. Дальше вступает теорема Гурвица, согласно которой алгебра А изоморфна одной из четырех алгебр: действительных чисел, кватернионов, октав. В этом как раз и заключается обобщенная теорема Фробениуса.[7]
(ведь алгебра комплексных чисел, так же как и алгебра кватернионов, является нормированной), или (ab,ab)=(a,a)(b,b). Но это равенство как раз и означает нормированность алгебры А. Дальше вступает теорема Гурвица, согласно которой алгебра А изоморфна одной из четырех алгебр: действительных чисел, кватернионов, октав. В этом как раз и заключается обобщенная теорема Фробениуса.[7]
Приведем еще одно применение теоремы Гурвица (или тождества Гамильтона).
Теорема Лагранжа.
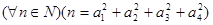 .
.
Лемма. Для любого простого числа p>2 найдется число  , такое что mp=a
, такое что mp=a 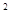 +b
+b 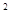 +c
+c 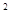 , a, b, c
, a, b, c  .
.
Доказательство:
Рассмотрим два множества чисел:
K={0, 1, 4,...,  }, L={-1-0, -1-1, -1-4,..., -1-
}, L={-1-0, -1-1, -1-4,..., -1-  }.
}.
В каждом из множеств числа попарно несравнимы по модулю p. В самом деле, возьмем  из множества K (или, эквивалентно, -1-k
из множества K (или, эквивалентно, -1-k  -1-k
-1-k 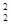 из множества L), где
из множества L), где  ,
,  . Если k
. Если k  k
k  (mod p), то (k
(mod p), то (k  +k
+k 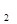 )(k
)(k  -k
-k 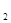 )
) 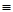 0 (mod p).. Но 0< k
0 (mod p).. Но 0< k  +k
+k  <p и 0<| k
<p и 0<| k  -k
-k  |<p, поскольку k
|<p, поскольку k  <p/2, k
<p/2, k  <p/2 и
<p/2 и  . Противоречие.
. Противоречие.
Всего в этих двух множествах p+1 чисел, следовательно, среди них найдутся сравнимые по модулю p, т. е. такие числа  из первого множества и
из первого множества и  из второго, что
из второго, что  . Откуда
. Откуда  для некоторого
для некоторого  . Теперь, поскольку k<p/2,
. Теперь, поскольку k<p/2,  <p/2, получаем mp=
<p/2, получаем mp=  <
< 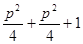 <
<  , а значит, m<p. Лемма доказана.
, а значит, m<p. Лемма доказана.
Доказательство теоремы Лагранжа:
Докажем, что любое простое число представимо в виде суммы четырех квадратов целых чисел. Для p=2 имеем  . Для p>2, по предыдущей лемме, найдется такое m<p, что число mp можно представить в виде mp=
. Для p>2, по предыдущей лемме, найдется такое m<p, что число mp можно представить в виде mp= 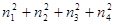 (n
(n  можно положить равным 0). Выберем теперь минимальное натуральное m, обладающее таким свойством. Покажем, что оно равно 1. Пусть m четно. Тогда либо все n
можно положить равным 0). Выберем теперь минимальное натуральное m, обладающее таким свойством. Покажем, что оно равно 1. Пусть m четно. Тогда либо все n 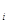 имеют одинаковую четность, либо среди них есть два четных и два нечетных (нумерация этих чисел не важна, поэтому пусть n
имеют одинаковую четность, либо среди них есть два четных и два нечетных (нумерация этих чисел не важна, поэтому пусть n 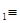 n
n 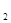 (mod 2), а n
(mod 2), а n  n
n  (mod 2). В обоих случаях числа
(mod 2). В обоих случаях числа
 являются целыми. Имеем:
являются целыми. Имеем:

 =
= 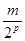 ,
,
значит, 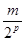 также представляется в виде суммы четырех квадратов целых чисел. Но
также представляется в виде суммы четырех квадратов целых чисел. Но  , а m, по предположению, минимальное число с таким свойством. Противоречие.
, а m, по предположению, минимальное число с таким свойством. Противоречие.
Пусть m нечетно. Тогда числа n 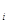 можно представить в виде n
можно представить в виде n 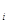 =q
=q 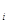 m+m
m+m 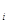 (
(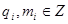 ). причем |m
). причем |m 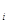 |<
|< 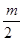 . Тогда
. Тогда
mp= 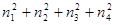 =sm+
=sm+ 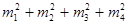 ,
,
где s - некоторое целое число.
Следовательно, 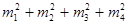 =mn, где n - неотрицательное целое число. Если n=0, то все m
=mn, где n - неотрицательное целое число. Если n=0, то все m 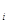 =0, n
=0, n 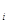 =q
=q 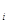 m, и тогда mp=
m, и тогда mp=  =m
=m 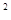 k, где k - натуральное, т. е. p=mk, m<p, а это означает, что m=1. Предположим теперь, что n
k, где k - натуральное, т. е. p=mk, m<p, а это означает, что m=1. Предположим теперь, что n  1. По теореме Гурвица получаем
1. По теореме Гурвица получаем
(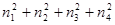 )(
)(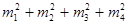 )=
)=  , где
, где
s  =
= 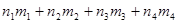 ,
,
s  =
= 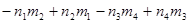 ,
,
s  =
=  ,
,
s  =
=  .
.
По определению, m  n
n 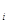 (mod m), т. е. s
(mod m), т. е. s 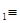
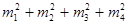
 0(mod m) и, значит,
0(mod m) и, значит,  . Аналогично доказывается, что
. Аналогично доказывается, что  при i=2, 3, 4. Но тогда (в силу неравенств |m
при i=2, 3, 4. Но тогда (в силу неравенств |m 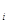 |<
|<  ) получаем: nm=
) получаем: nm= 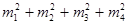
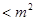 , т. е. n<m, и в итоге mp*nm=
, т. е. n<m, и в итоге mp*nm=  , откуда np=
, откуда np=  , что противоречит минимальности m. Итак, всякое простое число можно представить в виде суммы четырех квадратов целых чисел. Тогда, по теореме Гурвица, и любое составное число представимо в таком виде. Наконец, 1=
, что противоречит минимальности m. Итак, всякое простое число можно представить в виде суммы четырех квадратов целых чисел. Тогда, по теореме Гурвица, и любое составное число представимо в таком виде. Наконец, 1=  . Теорема доказана.[6]
. Теорема доказана.[6]
Пример 3.

Заключение
Мы рассмотрели различные системы «чисел», которые можно построить, исходя из действительных чисел, путем добавления рядя «мнимых единиц». Доказали, что существуют тождества с большим, чем 2, числом квадратов и описали их (теорема Гурвица). Было выяснено, что
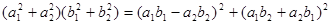
 +
+ 

=  +
+
 +
+

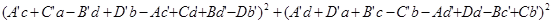
Так же было найдено приложение теоремы Гурвица.
Я добилась целей, которые перед собой поставила.
Список используемой литературы
1. Charles W. Curtis “Linear algebra” An Introductory Approach (Fourth Edition), Springer Verlag, 1984, xvii - 347 pp.
2. Rowe David E. “Jewish Mathematics” at Göttingen in the Era of Felix Klein. Isis, Vol. 77, No. 3, (Sep., 1986) – 432 pp
3. Калужин Л. А. “Основная теорема арифметики, Популярные лекции по математике” М.: Наука, 1969 г. - 32 стр.
4. Кантор И.Л., Солодовников А.С. “Гиперкомплексные числа” М.: Наука, 1973. - 144 с.
5. Тиморин В.А. “Квадратичная математика” - 2005
6. Тихомиров В. М. “ Великие математики прошлого и их великие теоремы” М.: МЦНМО, 2003.- 16 с.
7. Херстейн И. “Некоммутативные кольца” М.: Мир, 1972. - 192 c.