Лекция №5 (продолжение)
Скалярное произведение векторов
I. Определение
def. Скалярным произведением векторов  и
и 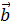 называется число, равное произведению модулей этих векторов на косинус угла между ними.
называется число, равное произведению модулей этих векторов на косинус угла между ними.
 . (1)
. (1)
Придадим (1) другой вид (по свойству 1 проекций).
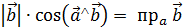 - проекция
- проекция 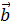 на ось, определяемую
на ось, определяемую  .
.
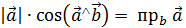 - проекция
- проекция  на ось, определяемую
на ось, определяемую 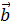 .
.
 . (2)
. (2)
II. Свойства скалярного произведения
1. Коммутативность умножения:  .
.
Доказательство. Справедливость утверждения непосредственно следует из определения скалярного произведения.
2. Ассоциативность относительно скалярного множителя:
 .
.
Доказательство.
1) Пусть 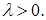 Тогда
Тогда




2)  Доказать самостоятельно.
Доказать самостоятельно.
3. Дистрибутивность умножения относительно сложения:

Доказательство.
Пример 7.1. Векторы  и
и 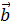 образуют угол
образуют угол  Зная, что
Зная, что  вычислить
вычислить 
Условие перпендикулярности векторов
По определению 
 , если
, если  или
или  , или
, или  , т.е.
, т.е. 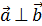 . Пусть
. Пусть  и
и  – ненулевые векторы. Тогда
– ненулевые векторы. Тогда
 .
.
Итак, для того, чтобы два ненулевых вектора были перпендикулярны, необходимо и достаточно, чтобы их скалярное произведение равнялось нулю.

Пример 7.2. При каком значении  векторы
векторы  и
и  ортогональны, если
ортогональны, если  ? Ответ:
? Ответ: 
III. Скалярное произведение векторов, заданных координатами
Даны два вектора  = ax
= ax  + ay
+ ay  + az
+ az  и
и 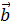 = bx
= bx  + by
+ by  + bz
+ bz  . Найти
. Найти  .
.
Найдем предварительно скалярное произведение ортов.


Тогда


 - скалярное произведение векторов, заданных координатами.
- скалярное произведение векторов, заданных координатами.
Если 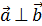 , то
, то 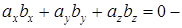 условие перпендикулярности векторов, заданных координатами.
условие перпендикулярности векторов, заданных координатами.
Пример 7.3. При каком значении c векторы 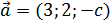 и
и  взаимно перпендикулярны.
взаимно перпендикулярны.
IV. Угол между векторами в пространстве
По определению  , значит
, значит
 .
.
Если векторы заданы координатами, т. е.  = ax
= ax  + ay
+ ay  + az
+ az  и
и 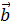 = bx
= bx  + by
+ by  + bz
+ bz  , то
, то

 .
.
Пример 7.4. Даны вершины четырехугольника А (1, -2, 2), В (1, 4, 0), С (-4, 1, 1),
D (-5, -5, 3). Вычислить угол  между его диагоналями. Ответ:
между его диагоналями. Ответ: 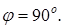
V. Приложение скалярного произведения к механике
Если материальна точка, на которую действует сила  совершает перемещение по вектору
совершает перемещение по вектору  , то работа А равна скалярному произведению
, то работа А равна скалярному произведению  и
и  .
.
 .
.
Пример 7.5. Вычислить работу равнодействующей  сил
сил 

 приложенных к материальной точке, которая под их воздействием перемещается прямолинейно из т. М1 (4, 2, -3) в т. М2 (7, 4, 1).
приложенных к материальной точке, которая под их воздействием перемещается прямолинейно из т. М1 (4, 2, -3) в т. М2 (7, 4, 1).
Решение.  ,
, 

Векторное произведение векторов
I. Определение
def. Векторным произведением вектора  на вектор
на вектор 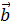 называется вектор
называется вектор  , который определяется следующим образом:
, который определяется следующим образом:
1) модуль вектора  численно равен площади параллелограмма, построенного на векторах
численно равен площади параллелограмма, построенного на векторах  и
и 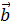 как на сторонах
как на сторонах
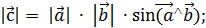
2) вектор  перпендикулярен перемножаемым векторам, т. е.
перпендикулярен перемножаемым векторам, т. е. 
3) направление вектора  таково, что если смотреть с его конца (вдоль вектора), то поворот по кратчайшему пути от вектора
таково, что если смотреть с его конца (вдоль вектора), то поворот по кратчайшему пути от вектора  к вектору
к вектору 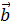 виден совершающимся против часовой стрелки.
виден совершающимся против часовой стрелки.
( ориентированы как
ориентированы как 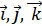 - прав. тройка).
- прав. тройка).
Обозначается:  или
или  .
.
 Частные случаи:
Частные случаи: 
 |
II. Свойства векторного произведения
1. При перестановке сомножителей векторное произведение меняет знак

Доказательство. Пусть  Тогда
Тогда
1)  , так как равны площади параллелограммов, построенных на векторах
, так как равны площади параллелограммов, построенных на векторах  и
и 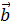 ;
;
2) Векторы  и
и  перпендикулярны векторам
перпендикулярны векторам  и
и 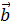 ;
;
3) Векторы  и
и  коллинеарны, но противоположно направлены.
коллинеарны, но противоположно направлены.
Из (1)-(3) следует, что  , то есть
, то есть 
2.  - ассоциативность относительно скалярного множителя, т.е. числовой множитель можно выносить за знак векторного произведения.
- ассоциативность относительно скалярного множителя, т.е. числовой множитель можно выносить за знак векторного произведения.
3.  - дистрибутивность векторного умножения относительно сложения.
- дистрибутивность векторного умножения относительно сложения.
4. Условие коллинеарности векторов. Векторное произведение равно нулевому вектору, если хотя бы один из перемножаемых векторов нулевой или синус угла между ними равен нулю, т.е. векторы коллинеарны.
Итак, для того, чтобы два ненулевых вектора были коллинеарны, необходимо и достаточно, чтобы их векторное произведение равнялось нулевому вектору.
