Раздел VI. ОБЫКНОВЕННЫЕ ДИФФЕРЕНЦИАЛЬНЫЕ УРАВНЕНИЯ
Лекция 6. МЕТОДЫРЕШЕНИЯ ОБЫКНОВЕННЫХ ДИФФЕРЕНЦИАЛЬНЫХ УРАВНЕНИЙ
Обыкновенным дифференциальным уравнением называется соотношение между неизвестной функцией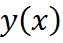 
и её производными, то есть 
.
Обыкновенными дифференциальными уравнениями можно описать задачи движения системы взаимодействующих материальных точек, химической кинетики, электрических цепей, сопротивления материалов (например, статический прогиб упругого стержня). Ряд важных задач для уравнений в частных производных также сводится к задачам для обыкновенных дифференциальных уравнений. Так бывает, если многомерная задача допускает разделение переменных (например, задачи на нахождение собственных колебаний упругих балок и мембран простейшей формы, или определение спектра собственных значений энергии частицы в сферически-симметричном поле), или если ее решение зависит только от некоторой комбинации переменных (так называемые автомодельные решения). Таким образом, решение обыкновенных дифференциальных уравнений занимает важное место среди прикладных задач физики, химии и техники.
Различают три основных типа задач для обыкновенных дифференциальных уравнений: задача Коши, краевые задачи и задачи на собственные значения.
Решением, интегралом или интегральной кривой уравнения или 
называется дифференцируемая функция, удовлетворяющая этому уравнению, т.е. такая, что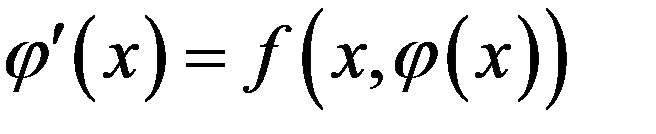 
тождественно по х на некотором участке изменения х.
Рассмотрим уравнени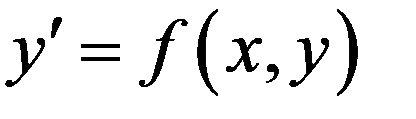е 
, где 
определена в некоторой области G плоскости Оху. Пусть в каждой точке (х, у) этой области определён такой угол 
, что
Точка (х, у) вместе с отрезком малой длины, составляющим угол 
с положительным направлением оси Ох, называется линейным элементом. Совокупность линейных элементов образует поле направлений, наглядно изображающих данное дифференциальное уравнение (см. рис.18.1). Интегральная кривая – это такая гладкая кривая, которая «согласована» с данным полем направлений, т.е. которая имеет в каждой своей точке касательную, предписанную этим полем.
Методы решения обыкновенных дифференциальных уравнений можно разбить на точные, приближенные и численные. К точным относятся методы, позволяющие выразить решение дифференциального уравнения через элементарные функции, либо представить его при помощи квадратур от элементарных функций. Эти методы изучаются в курсах обыкновенных дифференциальных уравнений. Нахождение точного решения задачи Коши облегчает качественное исследование этого решения и дальнейшие действия с ним.
Например, уравнение 
интегрируется точно: методом разделения переменных
; 
; 
.
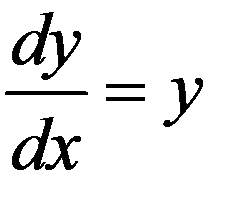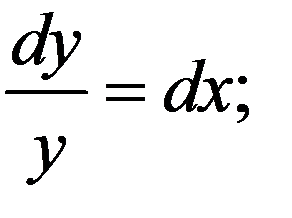
Однако, классы уравнений, для которых разработаны методы получения точных решений, сравнительно узки и охватывают только малую часть возникающих на практике задач. Например, доказано, что решение несложного уравнения 
(18.3)
не выражается через элементарные функции. А уравнение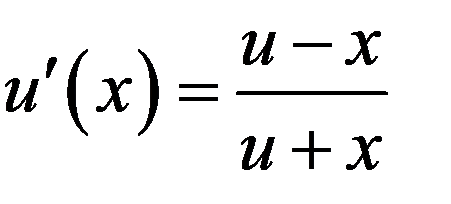 
(18.4)
можно точно проинтегрировать и найти общее решение 
.
(18.5)
Однако для того, чтобы составить таблицу значений u (х), надо численно решать трансцендентное уравнение (18.5), а это нисколько не проще, чем непосредственно численно проинтегрировать уравнение (18.4).
Приближенными называются методы, в которых решение получается как предел u (х) некоторой последовательности yn (x), причем yn (x) выражаются через элементарные функции или при помощи квадратур. Ограничиваясь конечным числом n, получаем приближенное выражение для u (х). Примером может служить метод разложения решения в обобщенный степенной ряд, рассматриваемый в курсах обыкновенных дифференциальных уравнений. Однако эти методы удобны лишь в том случае, когда большую часть промежуточных выкладок удается сделать точно (например, найти явное выражение коэффициентов ряда). Это выполнимо лишь для сравнительно простых задач (таких как линейные), что сильно сужает область применения приближенных методов.
Численные методы их еще называют сеточными (или конечно-разностными) – это алгоритмы вычисления приближенных (а иногда и точных) значений искомого решения u (х) на некоторой выбранной сетке значений аргумента хn. Решение при этом получается в виде таблицы. Численные методы не позволяют найти общего решения системы (18.1, 18.2); они могут дать только какое-то частное решение, например, решение задачи Коши. Это основной недостаток численных методов. Зато эти методы применимы к очень широким классам уравнений и всем типам задач для них. Поэтому с появлением быстродействующих ЭВМ численные методы решения стали одним из основных способов решения конкретных практических задач для обыкновенных дифференциальных уравнений.